Оглавление:

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств. Линейное программирование (ЛП) является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Линейное программирование
Создание Данцигом в конце 1940-х годов симплекс-метода стало началом современной эры в оптимизации. Этот метод позволил экономистам формулировать большие модели и систематически и эффективно анализировать их. Открытие Данцига совпало с появлением цифровых компьютеров, и симплекс-метод стал одним из первых примеров удачного использования этой новой революционной технологии. С тех пор реализация симплекс-метода постоянно совершенствуется. Сегодня линейное программирование и симплекс-метод — наиболее широко используемые средства оптимизации, и, несмотря на то что в настоящее время появились новые классы эффективных методов (например, метод внутренней точки), актуальность и важность симплекс-метода гарантированы в обозримом будущем.
Возможно эта страница вам будет полезна:
| Предмет математическое программирование |
Постановка задачи линейного программирования. Общая, нормальная и каноническая формы записи
Задача оптимизации, в которой требуется найти числа 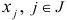 , обращающие в максимум (минимум) линейную форму
, обращающие в максимум (минимум) линейную форму
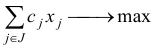
при линейных ограничениях (типа равенств и неравенств)
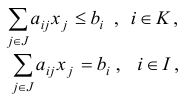
называется общей задачей линейного программирования (ЛП). Здесь . 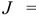
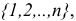
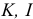 — некоторые заданные конечные наборы индексов;
— некоторые заданные конечные наборы индексов; 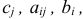
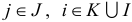 — заданные числа.
— заданные числа.
Задача, в которой требуется найти максимум линейной формы (1.1) при условиях (1.2) и условиях
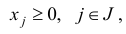
называется задачей линейного программирования в нормальной форме. В матричном виде задача в нормальной форме записи имеет вид
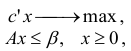
где 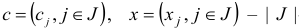 -векторы;
-векторы; 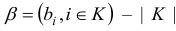 вектор;
вектор; 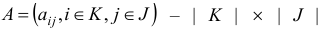 (-матрица; символом
(-матрица; символом 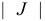 обозначено количество элементов множества
обозначено количество элементов множества 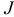 ; символом % (штрих) обозначается операция транспонирования.
; символом % (штрих) обозначается операция транспонирования.
Задача, в которой максимизируется линейная форма (1.1) при условиях (1.3) и (1.4), называется задачей линейного программирования в канонической форме записи.
В матричном виде задача в канонической форме записывается следующим образом
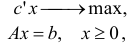
где 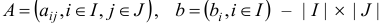 — матрица и
— матрица и 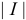 — вектор.
— вектор.
В задачах (1.5), (1.6) ограничения 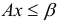 и
и 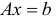 называются основными, ограничения вида
называются основными, ограничения вида 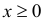 — прямыми. Линейная форма
— прямыми. Линейная форма 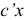 называется целевой функцией. Столбцы
называется целевой функцией. Столбцы 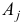 матрицы
матрицы 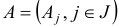 называются векторами условий.
называются векторами условий.
Вектор 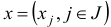 , удовлетворяющий всем ограничениям задачи линейного программирования, назовем ее планом. План
, удовлетворяющий всем ограничениям задачи линейного программирования, назовем ее планом. План 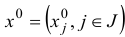 , обращающий в максимум линейную форму
, обращающий в максимум линейную форму 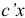 , называется оптимальным планом или решением задачи линейного программирования.
, называется оптимальным планом или решением задачи линейного программирования.
Задачу линейного программирования, заданную в любой форме, можно свести к задаче в канонической форме записи.
Покажем на простых примерах, как задачу, заданную в общей форме, можно свести к канонической.
Возможно эта страница вам будет полезна:
| Решение задач по математическому программированию |
Задача №1
Привести к канонической форме записи задачу
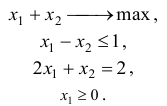
Решение:
Для того чтобы первое ограничение записать в форме равенства, введем неотрицательную переменную 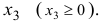 Заменим переменную
Заменим переменную 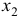 , на значения которой не наложено требование отрицательности, разностью двух неотрицательных переменных
, на значения которой не наложено требование отрицательности, разностью двух неотрицательных переменных
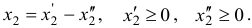
После этих преобразований исходная задача запишется в канонической форме
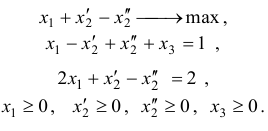
Задача №2
Привести к канонической форме задачу
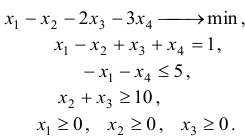
Решение:
Умножим коэффициенты целевой функции (а) на (-1), в результате вместо задачи минимизации получим задачу максимизации:
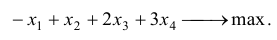
Введем дополнительные неотрицательные переменные 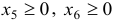 и запишем ограничения (с) и (d) в виде
и запишем ограничения (с) и (d) в виде
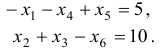
Исключим из задачи переменную 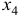 , на которую не наложено условие неотрицательности. Для этого из условия (Ь) выразим
, на которую не наложено условие неотрицательности. Для этого из условия (Ь) выразим 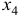 :
:
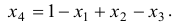
Подставив (h) в (f), (g), получим каноническую форму задачи :
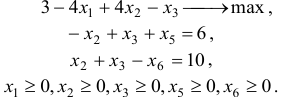
Отметим что задача максимизации функции (i) эквивалентна максимизации функции
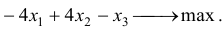
Задача линейного программирования в нормальной форме записи (1.5) приводится к канонической форме путем добавления неотрицательных переменных 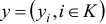 . В результате получим эквивалентную задачу в канонической форме
. В результате получим эквивалентную задачу в канонической форме
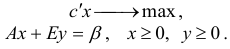
Здесь 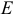 — единичная
— единичная 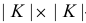 — матрица.
— матрица.
Теорема. Для того чтобы задача линейного программирования имела решение, необходимо и достаточно, чтобы множество ее планов было не пусто, а целевая функция ограничена сверху на множестве планов.
Таким образом, для построения решения задачи линейного программирования надо определить, какая из ситуаций 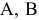 или
или 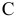 имеет для нее место, и, если реализовалась ситуация
имеет для нее место, и, если реализовалась ситуация 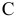 , то найти оптимальный план
, то найти оптимальный план 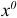 .
.
Возможно эта страница вам будет полезна:
| Примеры решения задач по математическому программированию |
Базисный план задачи линейного программирования
Выше показано, что любая задача линейного программирования может быть приведена к канонической форме. Поэтому далее основные теоремы и алгоритмы будут рассмотрены применительно к задаче (1.6), что не снижает общности рассмотрения.
Исследуем задачу линейного программирования в канонической форме (1.6), считая для определенности, что
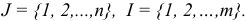
В дальнейшем, вплоть до подразд. 1.6, мы будем предполагать, что
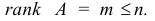
Очевидно, что при нарушении условия (1.8) система 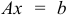 либо несовместна, либо содержит линейно зависимые условия, которые можно исключить из рассмотрения (см. подразд. 1.6).
либо несовместна, либо содержит линейно зависимые условия, которые можно исключить из рассмотрения (см. подразд. 1.6).
План 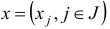 задачи (1.6) назовем базисным планом, если существует такое подмножество
задачи (1.6) назовем базисным планом, если существует такое подмножество 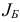 множества индексов
множества индексов 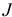 , что 1)
, что 1) 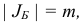 , 2)
, 2) 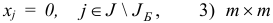 — матрица
— матрица 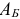 , построенная по правилу
, построенная по правилу 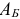
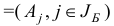 , не вырождена.
, не вырождена.
Напомним, что 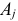 — это
— это 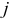 -й столбец матрицы
-й столбец матрицы 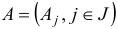 .
.
Множество 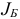 назовем базисом или множеством базисных индексов. Множество
назовем базисом или множеством базисных индексов. Множество 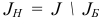 и будем называть множеством небазисных индексов, матрицу
и будем называть множеством небазисных индексов, матрицу  — базисной матрицей.
— базисной матрицей.
Иногда базисный план удобно обозначать в виде пары 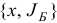 , состоящей из плана
, состоящей из плана 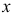 и соответствующего ему базиса
и соответствующего ему базиса 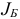 .
.
Базисный план считается невырожденным, если
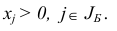
Отметим, что в общем случае плану 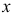 можно приписать несколько наборов базисных индексов
можно приписать несколько наборов базисных индексов
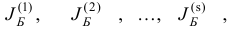
удовлетворяющих условиям 1) — 3). Базисному плану 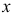 соответствует единственный набор базисных индексов
соответствует единственный набор базисных индексов 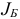 , если имеют место неравенства (1.9), т.е. базисный план является невырожденным.
, если имеют место неравенства (1.9), т.е. базисный план является невырожденным.
Легко проверить, что по заданному набору базисных индексов 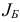 базисный план
базисный план 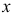 восстанавливается однозначно по правилу
восстанавливается однозначно по правилу
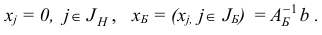
Здесь 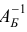 — матрица, обратная к базисной матрице
— матрица, обратная к базисной матрице 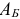 .
.
Далее будет показано, что симплекс-метод при решении задачи (1.6) генерирует последовательность планов 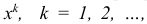 каждый из которых является базисным планом. Поскольку наша цель — построить последовательность планов, сходящихся к решению задачи (1.6), то итерации симплекс -метода будут иметь смысл только в том случае, если
каждый из которых является базисным планом. Поскольку наша цель — построить последовательность планов, сходящихся к решению задачи (1.6), то итерации симплекс -метода будут иметь смысл только в том случае, если
а) задача (1.6) имеет базисные планы;
б) существует оптимальный базисный план.
Оказывается, оба условия, а и б, верны при минимальных предположениях.
Теорема (основная теорема ЛП). Если для задачи (1.6) существует план, то для нее существует и базисный план. Если задача (1.6) имеет оптимальные планы, то хотя бы один из них базисный.
Возможно эта страница вам будет полезна:
| Заказать работу по математическому программированию |
Исследование базисного плана на оптимальность
Пусть 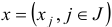 — базисный план задачи (1.6) с базисом
— базисный план задачи (1.6) с базисом 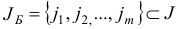 и базисной матрицей
и базисной матрицей 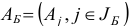 . Сформируем
. Сформируем 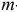 -вектор
-вектор 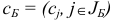 и подсчитаем
и подсчитаем 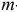 -вектор потенциалов
-вектор потенциалов 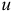 по правилу
по правилу
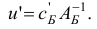
Вычислим оценки
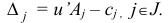
Отметим, что по построению
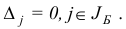
Для базисного плана 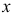 справедливы следующие утверждения.
справедливы следующие утверждения.
Утверждение 1. (Признак оптимальности базисного плана.) Базисный план х является решением задачи (1.6), если
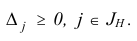
Утверждение 2. (Достаточное условие неограниченности сверху целевой функции.) Если существует индекс 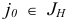 , для которого
, для которого 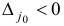 и все компоненты
и все компоненты 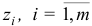 , вектора
, вектора
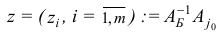
не положительны, то целевая функция задачи (1.6) не ограничена сверху на множестве планов.
Утверждение 3. (Возможность строгого улучшения плана.) Пусть 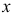 — невырожденный базисный план задачи (1.6) и для некоторого
— невырожденный базисный план задачи (1.6) и для некоторого 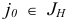 справедливы соотношения
справедливы соотношения
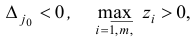
где вектор 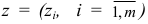 определен по формуле (1.10). Тогда существует базисный план
определен по формуле (1.10). Тогда существует базисный план 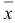 , для которого
, для которого 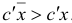 .
.
Компоненты нового базисного плана 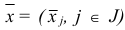 и соответствующий ему базис
и соответствующий ему базис 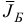 строятся по правилу
строятся по правилу
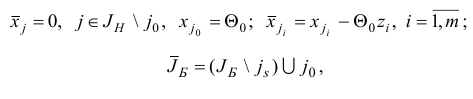
где
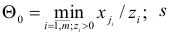
любой индекс из множества
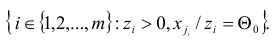
Задача №3
Исследовать на оптимальность план 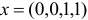 задачи
задачи
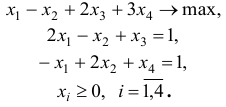
Решение:
В рассматриваемой задаче векторы условий 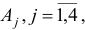 имеют вид
имеют вид
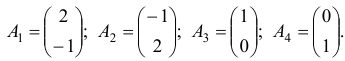
План 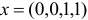 является невырожденным базисным планом с базисом
является невырожденным базисным планом с базисом 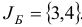 . Данному базису соответствует базисная матрица
. Данному базису соответствует базисная матрица

Для проверки плана  на оптимальность подсчитаем вектор потенциалов
на оптимальность подсчитаем вектор потенциалов 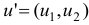 :
:
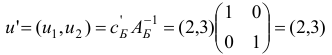
и оценки
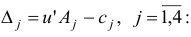
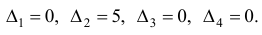
Поскольку все оценки 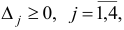 то, согласно утверждению 1, план
то, согласно утверждению 1, план 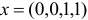 является оптимальным.
является оптимальным.
Возможно эта страница вам будет полезна:
| Помощь по математическому программированию |
Симплекс-метод. Общая итерация
Пусть 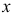 — некоторый базисный план задачи (1.6) с базисом
— некоторый базисный план задачи (1.6) с базисом 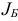 . В результате исследования, основанного на утверждениях 1-3, выясняется либо 1) оптимальность плана
. В результате исследования, основанного на утверждениях 1-3, выясняется либо 1) оптимальность плана 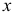 либо 2) неразрешимость задачи (1.6) в силу неограниченности сверху целевой функции на множестве планов, либо 3) возможность перехода к новому базисному плану
либо 2) неразрешимость задачи (1.6) в силу неограниченности сверху целевой функции на множестве планов, либо 3) возможность перехода к новому базисному плану 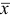 , для которого
, для которого 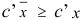 .
.
Последовательный переход от одного базисного плана к «лучшему» базисному плану вплоть до получения оптимального плана составляет основную идею симплекс-метода.
Для реализации симплекс-метода кроме исходных данных задачи (1.6) (векторов 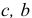 и матрицы
и матрицы 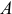 ) на каждой итерации необходимо знать следующие параметры:
) на каждой итерации необходимо знать следующие параметры:
текущий базисный план 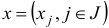 (достаточно знать только его базисные компоненты
(достаточно знать только его базисные компоненты 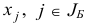 );
);
соответствующее плану 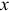 множество базисных индексов
множество базисных индексов 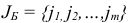 ;
; 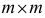 — матрицу
— матрицу 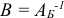 обратную к базисной матрице
обратную к базисной матрице 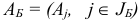 .
.
Опишем общую итерацию симплекс-метода по шагам. Шаг 1. Вычислим вектор потенциалов 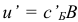 , где
, где 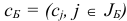 , и оценки
, и оценки
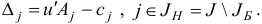
Шаг 2. Если 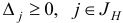 то STOP: вектор
то STOP: вектор 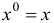 является оптимальным планом задачи (1.6). В противном случае переходим к шагу 3.
является оптимальным планом задачи (1.6). В противном случае переходим к шагу 3.
Шаг 3. Выберем индекс 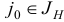 , для которого
, для которого 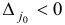 . Построим вектор
. Построим вектор 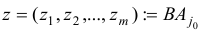 . Если
. Если 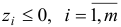 , то STOP: задача (1.6) не имеет решения в силу неограниченности сверху целевой функции на множестве планов. В противном случае перейдем к шагу 4.
, то STOP: задача (1.6) не имеет решения в силу неограниченности сверху целевой функции на множестве планов. В противном случае перейдем к шагу 4.
Шаг 4. Найдем минимум
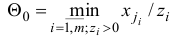
и выберем индекс 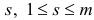 , для которого
, для которого 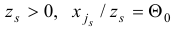 .
.
Шаг 5. Построим новый базисный план 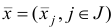 соответствующий ему базис
соответствующий ему базис 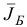 по правилам
по правилам
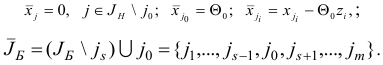
Шаг 6. Вычислим матрицу 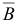 , обратную к новой базисной матрице
, обратную к новой базисной матрице 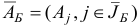 , по формуле
, по формуле 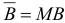 , где матрица
, где матрица 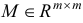 , отличается от единичной
, отличается от единичной 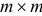 -матрицы только
-матрицы только 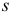 -м столбцом, который имеет вид
-м столбцом, который имеет вид
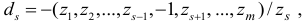
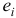 — единичный
— единичный 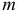 -вектор с единицей на
-вектор с единицей на 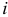 -м месте.
-м месте.
Переходим к следующей итерации, исходя из новых плана 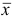 , базиса
, базиса 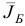 и матрицы
и матрицы 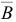 , обратной к новой базисной матрице
, обратной к новой базисной матрице 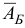 .
.
Замечания. 1. На шаге 3 выбирается индекс 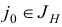 , для которого
, для которого 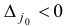 . В общем случае существует несколько индексов, удовлетворяющих этому условию. При численной реализации симплекс-метода для выбора
. В общем случае существует несколько индексов, удовлетворяющих этому условию. При численной реализации симплекс-метода для выбора 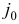 можно использовать дополнительные «уточняющие» правила, например, следующие:
можно использовать дополнительные «уточняющие» правила, например, следующие:
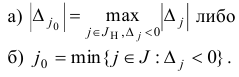
На шаге 4 выбирается индекс 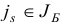 или
или 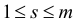 для которого
для которого 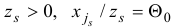 . В общем случае этот выбор может оказаться неоднозначным. Можно использовать дополнительные уточняющие правила, например, следующие:
. В общем случае этот выбор может оказаться неоднозначным. Можно использовать дополнительные уточняющие правила, например, следующие:
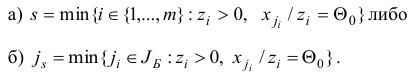
В современных версиях симплекс-метода для нахождения вектора потенциалов 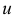 (см. шаг 1) и вектора
(см. шаг 1) и вектора 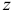 (см. шаг 3) решаются системы
(см. шаг 3) решаются системы 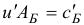 и
и 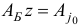 , соответственно. Для эффективного решения последних используется
, соответственно. Для эффективного решения последних используется 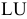 -разложение базисной матрицы
-разложение базисной матрицы 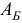 .
.
Легко подсчитать, что приращение целевой функции при переходе от начального базисного плана 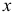 к новому базисному плану
к новому базисному плану 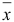 равно:
равно:

По построению,
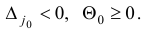
Следовательно, при 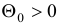 происходит «строгое улучшение» плана:
происходит «строгое улучшение» плана: 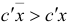 . Из описания шага 4 видно, что в случае невырожденности начального базисного плана
. Из описания шага 4 видно, что в случае невырожденности начального базисного плана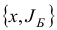 всегда верно неравенство
всегда верно неравенство 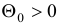 .
.
В случае, когда базисный план 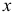 (с базисом
(с базисом 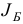 ) является вырожденным, может реализоваться ситуация:
) является вырожденным, может реализоваться ситуация: 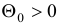 . При этом мы получаем
. При этом мы получаем 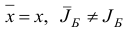 .
.
В этом случае не происходит улучшения целевой функции, но итерация может оказаться полезной, так как изменяется базис и новый базис может быть ближе к оптимальному базису, чем старый.
Задача №4
Решить задачу ЛП симплекс-методом
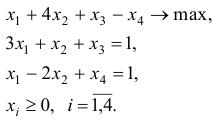
Решение:
Для данной задачи 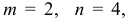 а векторы
а векторы 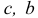 и матрица
и матрица 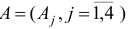 имеют вид
имеют вид 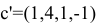 ;
;
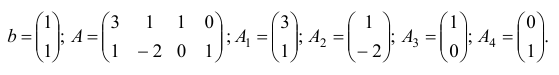
В качестве начального базисного плана возьмем вектор 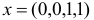 , которому соответствует базисное множество
, которому соответствует базисное множество 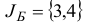 и базисная матрица
и базисная матрица
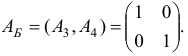
Используя
Очевидно, что
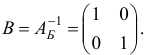
Используя
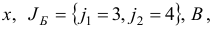
осуществим первую итерацию симплекс-метода. Шаг 1. Вычислим вектор потенциалов
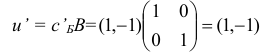
и оценки
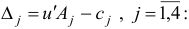
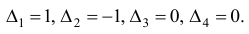
Шаг 2. Поскольку среди оценок 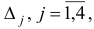 есть отрицательные, то переходим к шагу 3.
есть отрицательные, то переходим к шагу 3.
Шаг 3. Выберем в качестве индекса 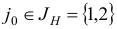 , для которого
, для которого 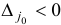 , индекс 2, т.е.
, индекс 2, т.е. 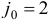 . Построим вектор
. Построим вектор
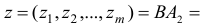
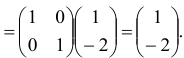
Поскольку среди компонент вектора 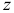 есть положительные, то перейдем к шагу 4. Шаг 4. Найдем минимум
есть положительные, то перейдем к шагу 4. Шаг 4. Найдем минимум
Очевидно, что в данном примере в качестве индекса 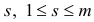 , для которого
, для которого 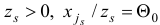 можно взять только индекс 1, т.е.
можно взять только индекс 1, т.е.
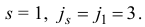
Шаг 5. Построим новый базисный план
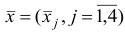
и соответствующий ему базис 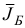 по правилам
по правилам
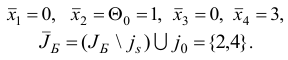
Шаг 6. Построим матрицу
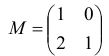
и найдем матрицу
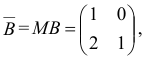
обратную к новой базисной матрице 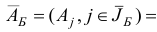
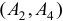 . Переходим ко второй итерации, исходя из новых плана
. Переходим ко второй итерации, исходя из новых плана 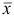 , базиса
, базиса 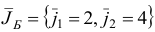 и матрицы
и матрицы 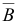 .
.
Осуществим вторую итерацию.
Шаг 1. Вычислим вектор потенциалов
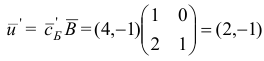
и оценки
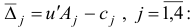
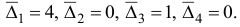
Шаг 2. Поскольку все оценки 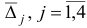 , неотрицательны, то алгоритм заканчивает свою работу: вектор
, неотрицательны, то алгоритм заканчивает свою работу: вектор 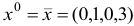 является оптимальным планом рассматриваемой задачи.
является оптимальным планом рассматриваемой задачи.
Возможно эта страница вам будет полезна:
| Задачи математического программирования |
Зацикливание. Конечные модификации симплекс- метода
Итерацию
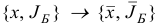
симплекс-метода назовем невырожденной, если 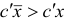 .
.
Ясно, что итерация 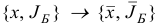 может оказаться вырожденной только в том случае, если базисный план
может оказаться вырожденной только в том случае, если базисный план 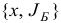 вырожденный, причем в случае вырожденности итерации справедливы соотношения:
вырожденный, причем в случае вырожденности итерации справедливы соотношения:
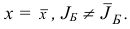
Теорема. При любом выборе начального базисного плана 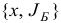 симплекс-метод за конечное число итераций строит оптимальный базисный план задачи (1.6) либо обнаруживает неограниченность сверху ее целевой функции на множестве планов, если в процессе его реализации не встречаются вырожденные итерации.
симплекс-метод за конечное число итераций строит оптимальный базисный план задачи (1.6) либо обнаруживает неограниченность сверху ее целевой функции на множестве планов, если в процессе его реализации не встречаются вырожденные итерации.
При наличии вырожденных итераций при реализации симплекс-метода может возникнуть такая ситуация, когда начиная с некоторого вырожденного базисного плана 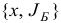 мы осуществляем последовательность вырожденных итераций
мы осуществляем последовательность вырожденных итераций
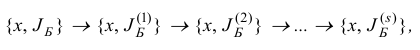
в которых меняются только базисы 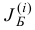 базисного плана
базисного плана 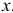 , причем при некотором конечном
, причем при некотором конечном 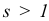 имеет место равенство
имеет место равенство 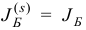 . Очевидно, что если мы продолжим операции симплекс-метода исходя из
. Очевидно, что если мы продолжим операции симплекс-метода исходя из 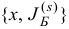 , то опять получим ту же последовательность итерации (1.12) и т. д. Такое явление получило название зацикливания.
, то опять получим ту же последовательность итерации (1.12) и т. д. Такое явление получило название зацикливания.
Первоначально считалось, что зацикливание — крайне редкое явление. Однако позже было замечено, что вероятность возникновения зацикливания увеличивается с ростом размеров задачи. Кроме того, зацикливание является типичным явлением для задач ЛП, возникающих при аппроксимации задач целочисленного программирования. В связи с этим возникла необходимость в разработке специальных приемов борьбы с зацикливанием. К настоящему времени известно много таких приемов. Опишем два из них.
- Стратегия возмущения (метод Чарнса). Предположим, что в задаче (1.6) мы возмутили вектор правых частей
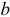 , заменив его на
, заменив его на 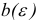 :
:
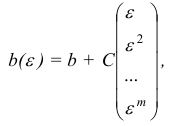
где 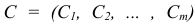 — некоторая невырожденная
— некоторая невырожденная 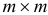 — матрица со столбцами
— матрица со столбцами 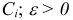 — достаточно малое число.
— достаточно малое число.
Возмущения в векторе 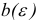 вызовут возмущения в базисных компонентах
вызовут возмущения в базисных компонентах 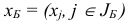 каждого базисного плана следующим образом:
каждого базисного плана следующим образом:
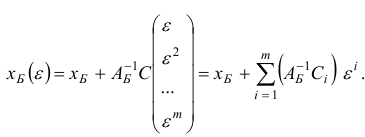
Матрица 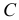 должна быть такой, что на первой итерации вектор
должна быть такой, что на первой итерации вектор 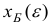 должен быть строго положительным при достаточно малых
должен быть строго положительным при достаточно малых 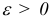 . Для этого достаточно положить
. Для этого достаточно положить 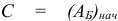 , где
, где 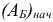 — базисная матрица, соответствующая начальному базису
— базисная матрица, соответствующая начальному базису 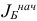 . Тогда для начального базисного плана имеем
. Тогда для начального базисного плана имеем
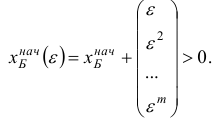
Предположим, что на текущей итерации имеется базисный план 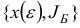 возмущенной задачи, для которого справедливы неравенства
возмущенной задачи, для которого справедливы неравенства 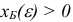 при достаточно малых
при достаточно малых 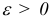 . Согласно данным подразд. 1.4, новый базисный план
. Согласно данным подразд. 1.4, новый базисный план 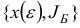 , построенный в результате одной итерации симплекс-метода из
, построенный в результате одной итерации симплекс-метода из 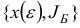 , будет также невырожденным, если не существует таких двух базисных индексов
, будет также невырожденным, если не существует таких двух базисных индексов 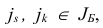 что
что 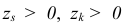 и
и
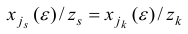
для всех достаточно малых 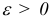 .
.
Последние соотношения могут иметь место только в том случае, если 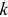 -я и
-я и 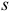 -я строки матрицы
-я строки матрицы 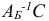 линейно зависимы. Однако это противоречит тому, что
линейно зависимы. Однако это противоречит тому, что 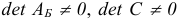 . Значит, соотношения (1.14) не могут иметь места и, следовательно, новый базисный план
. Значит, соотношения (1.14) не могут иметь места и, следовательно, новый базисный план 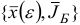 возмущенной задачи будет невырожденным при достаточно малых
возмущенной задачи будет невырожденным при достаточно малых 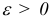 .
.
Таким образом, мы показали, что при достаточно малых 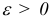 все итерации симплекс-метода для задачи с возмущенным вектором
все итерации симплекс-метода для задачи с возмущенным вектором 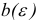 будут невырожденными и, следовательно, для возмущенной задачи симплекс- метод будет конечным. Кроме того справедлива следующая теорема.
будут невырожденными и, следовательно, для возмущенной задачи симплекс- метод будет конечным. Кроме того справедлива следующая теорема.
Теорема. Существует такое 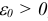 , что для любого
, что для любого 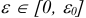 каждому базисному плану возмущенной задачи, порожденному базисом
каждому базисному плану возмущенной задачи, порожденному базисом 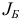 , соответствует базисный план (невозмущенной) исходной задачи, порожденный тем же базисом
, соответствует базисный план (невозмущенной) исходной задачи, порожденный тем же базисом 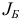 , а из оптимальности базиса
, а из оптимальности базиса 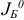 в возмущенной задаче следует его оптимальность в исходной задаче.
в возмущенной задаче следует его оптимальность в исходной задаче.
Покажем, как описанные выше результаты можно использовать для предотвращения зацикливания в исходной задаче (1.6).
Недостатком описанных выше рассуждений является то, что они верны только при достаточно малых 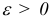 и заранее невозможно указать конкретное значение
и заранее невозможно указать конкретное значение 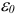 . Однако существуют правила (лексико-графическая стратегия), которые позволяют «мысленно» осуществить процедуру решения возмущенной задачи без явного выбора значения параметра
. Однако существуют правила (лексико-графическая стратегия), которые позволяют «мысленно» осуществить процедуру решения возмущенной задачи без явного выбора значения параметра 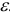 .
.
Пусть в начале текущей итерации для исходной задачи есть базисный план  , базис
, базис 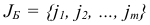 и соответствующая ему базисная матрица
и соответствующая ему базисная матрица 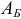 . Очевидно, что при достаточно малых
. Очевидно, что при достаточно малых 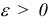 базис
базис 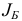 порождает базисный план
порождает базисный план 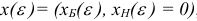 , где
, где 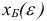 имеет вид (1.13), возмущенной задачи. Предположим, что мы осуществляем итерацию симплекс-метода для исходной и возмущенной задач, исходя из базисных планов
имеет вид (1.13), возмущенной задачи. Предположим, что мы осуществляем итерацию симплекс-метода для исходной и возмущенной задач, исходя из базисных планов 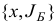 и
и 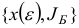 .
.
Ясно, что для обеих задач шаги 1-3 итерации будут полностью совпадать. Значит, совпадут и индексы 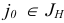 , подлежащие вводу в базис. Перейдем к шагу 4, на котором определяется индекс
, подлежащие вводу в базис. Перейдем к шагу 4, на котором определяется индекс 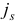 , подлежащий выводу из базиса
, подлежащий выводу из базиса 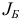 . Для возмущенной задачи индекс
. Для возмущенной задачи индекс 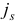 однозначно определяется из соотношений
однозначно определяется из соотношений
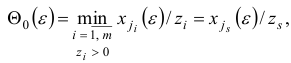
где 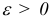 — достаточно малое число.
— достаточно малое число.
Легко проверить, что найти единственный индекс 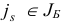 определяемый условием (1.15), можно по следующему правилу.
определяемый условием (1.15), можно по следующему правилу.
Положим
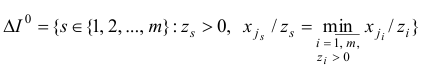
и построим множества 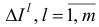 , по рекуррентным правилам
, по рекуррентным правилам
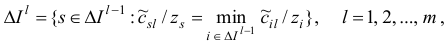
где
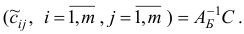
По построение,
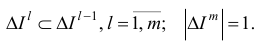
Обозначим через 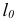 наименьший индекс
наименьший индекс 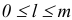 , при котором
, при котором 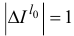 :
:
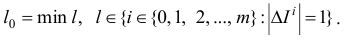
Пусть 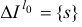 . Тогда индекс
. Тогда индекс 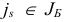 и совпадает с индексом, определяемым соотношениями (1.15).
и совпадает с индексом, определяемым соотношениями (1.15).
Ясно, что для исходной задачи любой индекс вида 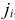 , где
, где  можно взять в качестве индекса, выводимого из базиса. Согласно (1.18)
можно взять в качестве индекса, выводимого из базиса. Согласно (1.18) 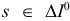 , следовательно, индекс
, следовательно, индекс 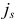 можно выводить из базиса в исходной задаче. Таким образом, в качестве нового базиса для исходной задачи можно взять базис
можно выводить из базиса в исходной задаче. Таким образом, в качестве нового базиса для исходной задачи можно взять базис
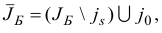
где индекс 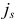 однозначно определяется по правилам (1.16)-(1.19). (Для возмущенной задачи новый базис (1.20) является единственно возможным).
однозначно определяется по правилам (1.16)-(1.19). (Для возмущенной задачи новый базис (1.20) является единственно возможным).
Из сказанного выше следует, что симплекс-метод будет конечным и для исходной задачи (1.6), если на шаге 4 индекс 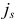 , подлежащий выводу из базиса, определять по правилам (1.16), (1.17), (1.19).
, подлежащий выводу из базиса, определять по правилам (1.16), (1.17), (1.19).
- Правило Блэнда. В 1977 г. Р. Блэнд предложил очень простое правило предотвращения зацикливания в симплекс- методе. Это правило сводится к следующему.
При реализации итерации симплекс-метода на шаге 3 индекс 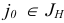 , подлежащий вводу в новый базис, однозначно определяется по правилу
, подлежащий вводу в новый базис, однозначно определяется по правилу
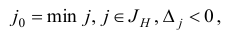
а на шаге 4 индекс 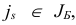 подлежащий выводу из базиса, однозначно определяется соотношениями
подлежащий выводу из базиса, однозначно определяется соотношениями
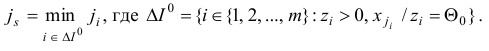
При использовании дополнительных правил (1.21), (1.22) симплекс-метод для любой задачи ЛП (с заданным начальным базисным планом) за конечное число итераций строит оптимальный базисный план либо обнаруживает неограниченность сверху целевой функции на множестве планов.
Первая фаза симплекс-метода
Все предыдущие утверждения и операции симплекс-метода были справедливы в предположении, что для задачи в канонической форме (1.6) выполнено условие (1.8).
Понятно, что для произвольной задачи (1.6) это условие может нарушаться. Поэтому, прежде чем применять описанный симплекс-метод необходимо исходную задачу (1.6) привести к такому виду, для которого выполняются соотношения (1.8).
Кроме того, из описания общей итерации симплекс-метода видно, что для начала его работы необходимо знать начальный базисный план 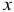 и начальный набор базисных индексов
и начальный набор базисных индексов 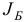 , для которых выполняются соотношения:
, для которых выполняются соотношения:
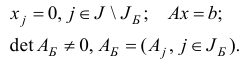
Проблема нахождения такой начальной информации может оказаться нетривиальной. Действительно, в общем случае по трудоемкости это проблема эквивалентна построению решения некоторой задачи линейного программирования. Для преодоления указанной трудности используется двухфазный симплекс-метод, общая схема которого состоит в следующем.
На первой фазе формируется вспомогательная задача ЛП, которая отличается от исходной задачи (1.6). Вспомогательная задача строится таким образом, что для нее выполняется условие (1.8), легко строится начальный базисный план и она имеет решение. Анализ решения вспомогательной задачи позволяет:
1) определить, совместны ли ограничения исходной задачи (1.6);
2) проверить, выполняется ли условие (1.8) для исходной задачи (1.6) и в случае его нарушения обнаружить линейно зависимые основные ограничения и удалить их из условий задачи;
3) в случае совместности ограничений задачи (1.6) построить для нее начальный базисный план 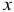 и базис
и базис 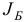 .
.
Если анализ решения вспомогательной задачи закончился построением начального базисного плана для исходной задачи, то переходим ко второй фазе алгоритма. Вторая фаза состоит в решении исходной задачи описанным выше симплекс-методом, при этом в качестве начальной используется информация, полученная на первой фазе.
Опишем подробнее первую фазу алгоритма. Без ограничения общности будем считать, что в задаче (1.6) вектор 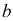 удовлетворяет неравенству
удовлетворяет неравенству 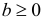 .
.
Тогда задачу первой фазы можно записать в виде
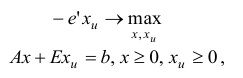
где 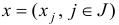 — исходные переменные,
— исходные переменные, 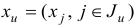 — искусственные переменные,
— искусственные переменные, 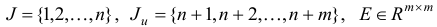 — единичная матрица,
— единичная матрица, 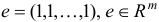 .
.
Легко проверить, что вектор 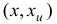 с компонентами
с компонентами
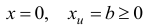
является базисным планом задачи (1.23) с базисом
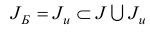
и базисной матрицей 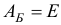 .
.
Решим задачу (1.23) симплекс-методом, описанным в подразд. 1.4, используя в качестве начального базисный план (1.24). Поскольку целевая функция задачи (1.23) ограничена сверху на множестве ее планов 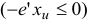 , то через конечное число итераций будет построен оптимальный базисный план
, то через конечное число итераций будет построен оптимальный базисный план 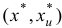 задачи (1.23) и соответствующий ему базис
задачи (1.23) и соответствующий ему базис 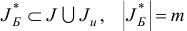 . Справедлива следующая теорема
. Справедлива следующая теорема
Теорема. Ограничения исходной задачи (1.6) совместны тогда и только тогда, когда компонента 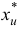 оптимального базисного плана задачи (1.23) равна нулю.
оптимального базисного плана задачи (1.23) равна нулю.
Проведем анализ решения задачи (1.23). Возможны случаи:
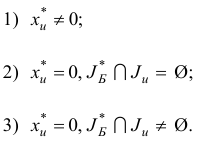
Пусть реализовался случай 1. Прекращаем исследование исходной задачи (1.6), так как согласно теореме она не имеет планов.
Рассмотрим случай 2. Легко проверить, что вектор 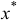 с базисным множеством
с базисным множеством 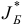 является базисным планом задачи (1.6). Переходим ко второй фазе алгоритма, исходя из этого плана.
является базисным планом задачи (1.6). Переходим ко второй фазе алгоритма, исходя из этого плана.
Исследуем случай 3. Ясно, что вектор 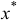 является планом задачи (1.6), но множество
является планом задачи (1.6), но множество 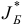 не является его базисом для задачи (1.6). Попытаемся построить базис для плана в задаче (1.6).
не является его базисом для задачи (1.6). Попытаемся построить базис для плана в задаче (1.6).
Пусть
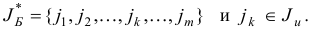
Обозначим
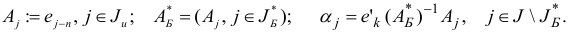
Возможны под случаи:
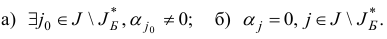
Если реализовался подслучай а, то оптимальному плану 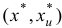 задачи (1.23) припишем новый базис
задачи (1.23) припишем новый базис
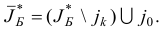
Очевидно, что по построению,
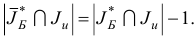
Снова проверяем, какая из ситуаций, 2 или 3, имеет место для оптимального плана 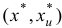 задачи (1.23) и нового базиса (1.26).
задачи (1.23) и нового базиса (1.26).
Подслучай б означает, что в исходной задаче (1.6) основное ограничение с индексом 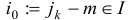 является линейно зависимым с остальными основными ограничениями этой задачи. Множество планов задачи (1.6) не изменится, если мы удалим это ограничение, т.е. заменим множество индексов
является линейно зависимым с остальными основными ограничениями этой задачи. Множество планов задачи (1.6) не изменится, если мы удалим это ограничение, т.е. заменим множество индексов 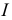 на
на 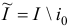 . Для преобразованной задачи (1.6) вспомогательная задача первой фазы получится из задачи (1.23) после удаления ограничения с индексом
. Для преобразованной задачи (1.6) вспомогательная задача первой фазы получится из задачи (1.23) после удаления ограничения с индексом 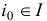 и искусственной переменной
и искусственной переменной 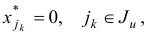 , т.е. заменой множеств
, т.е. заменой множеств 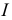 и
и 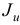 на
на
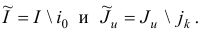
Очевидно, что для новой задачи первой фазы вектор
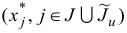
является оптимальным базисным планом с базисом
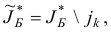
для которого
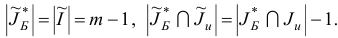
Для плана
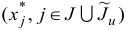
и новых множеств 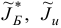 вновь проверяем, какая из ситуаций,
вновь проверяем, какая из ситуаций,
2 или 3, имеет место.
Ясно, что не более чем через 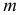 шагов из основных ограничений задачи (1.6) будут исключены все линейно зависимые ограничения и она будет сведена к задаче
шагов из основных ограничений задачи (1.6) будут исключены все линейно зависимые ограничения и она будет сведена к задаче
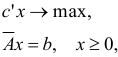
где
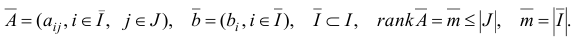
При этом для задачи (1.27) будет построен базисный план 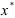 с некоторым базисом
с некоторым базисом
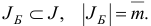
Дальнейшее решение задачи (1.27) осуществляем симплекс-методом, описанным в подразд. 1.4, используя в качестве начальных построений базисный план 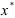 с базисом
с базисом 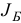 .
.
Возможно эта страница вам будет полезна:
| Решение задач по линейному программированию |
Теория двойственности в линейном программировании
Определение двойственной задачи. Соотношения двойственности
Рассмотрим задачу линейного программирования, заданную в произвольной форме записи:
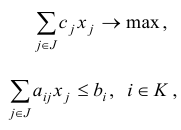
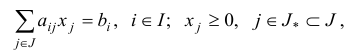
где 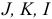 — некоторые конечные множества индексов. Задачу линейного программирования
— некоторые конечные множества индексов. Задачу линейного программирования
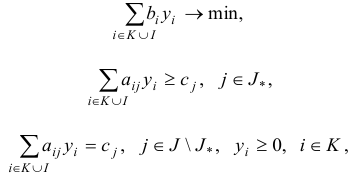
назовем двойственной по отношению к задаче (2.1). При этом задача (2.1) считается прямой.
Из приведенного определения следует, что для задачи линейного программирования в нормальной форме
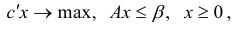
двойственной является задача
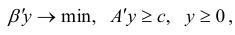
а для задачи в канонической форме
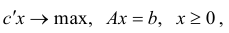
двойственная задача имеет вид
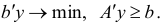
Легко проверить, что если в качестве исходной взять задачу линейного программирования (2.2), то двойственной к ней будет задача (2.1).
Сравнивая пары двойственных задач (2.1) и (2.2), приходим к следующему правилу построения двойственной задачи:
- Двойственная задача является задачей минимизации линейной формы, коэффициенты которой совпадают с коэффициентами вектора условий прямой задачи.
- Каждому
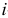 -му основному ограничению прямой задачи соответствует
-му основному ограничению прямой задачи соответствует 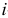 -я переменная
-я переменная 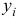 двойственной задачи. При этом для
двойственной задачи. При этом для 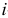 -й переменной
-й переменной 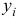 двойственной задачи выполняются соотношения:
двойственной задачи выполняются соотношения:
а) она не имеет ограничений на знак, если 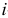 -е основное ограничение прямой задачи имело вид равенства;
-е основное ограничение прямой задачи имело вид равенства;
б) 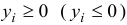 , если
, если 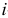 -е основное ограничение прямой задачи имело вид неравенства
-е основное ограничение прямой задачи имело вид неравенства 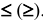 .
.
Каждой 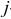 -й переменной
-й переменной 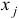 прямой задачи соответствует
прямой задачи соответствует 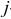 -е основное ограничение двойственной задачи. При этом вид
-е основное ограничение двойственной задачи. При этом вид 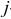 -го основного ограничения двойственной задачи определяется условиями:
-го основного ограничения двойственной задачи определяется условиями:
а) оно имеет вид равенства, если переменная 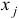 в прямой задаче не имеет ограничений на знак;
в прямой задаче не имеет ограничений на знак;
б) оно имеет вид неравенства 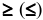 если в прямой задаче переменная
если в прямой задаче переменная 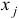 имела ограничение
имела ограничение 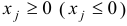 на знак.
на знак.
Рассмотрим общую задачу линейного программирования (2.1) и двойственную к ней задачу (2.2). Назовем эти задачи парой двойственных задач.
Теорема. Если одна из задач двойственной пары имеет решение, то другая задача также имеет решение. При этом для любых оптимальных планов
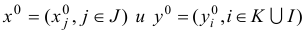
имеет место равенство
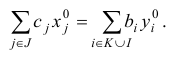
Следствие 1. Для разрешимости одной из задач двойственной пары необходимо и достаточно, чтобы каждая из задач этой пары имела хотя бы один план.
Следствие 2. Для того чтобы одна из задач двойственной пары имела планы, а множество планов другой задачи было пусто, необходимо и достаточно, чтобы целевая функция первой задачи была не ограничена на множестве ее планов.
Следствие 3. Для любых планов
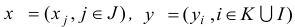
задач двойственной пары справедливо неравенство
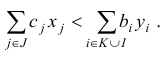
Следствие 4. Для оптимальности планов
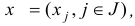
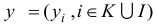
задач двойственной пары необходимо и достаточно выполнение равенства
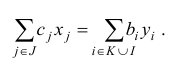
Задача №5
Записать задачу, двойственную к данной
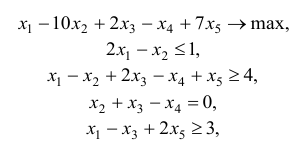
Решение:
Чтобы записать задачу, двойственную к данной, приведем систему к виду (2.1)
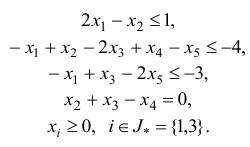
Теперь воспользуемся определением (2.2) и запишем задачу, двойственную к данной
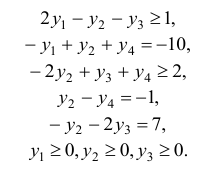
Базисный двойственный базисный план
Далее для определенности будем рассматривать пару двойственных задач (2.5), (2.6), в которой прямая задача имеет каноническую форму записи (2.5) с матрицей
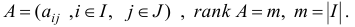
Вектор 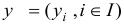 назовем двойственным планом, если
назовем двойственным планом, если 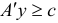 .
.
Двойственный план 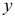 называется базисным двойственным планом, если существует такое множество
называется базисным двойственным планом, если существует такое множество 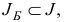 что
что
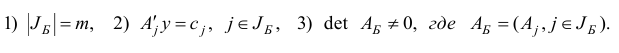
Как и раньше, множество 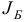 будем называть базисом или множеством базисных индексов, матрицу
будем называть базисом или множеством базисных индексов, матрицу 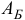 — базисной матрицей.
— базисной матрицей.
Отметим, что двойственный базисный план однозначно восстанавливается по заданному базису:
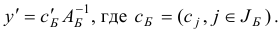
Базисный двойственный план у считается невырожденным, если
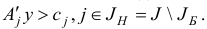
Пусть 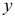 — базисный двойственный план с базисом
— базисный двойственный план с базисом 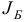 .
. 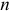 -вектор
-вектор 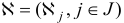 с компонентами, построенными по правилу
с компонентами, построенными по правилу
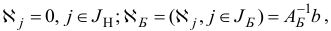
назовем псевдопланом задачи (2.5), соответствующим базису 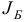 .
.
Утверждение 1. Если среди базисных компонент псевдоплана 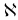 нет отрицательных, т. е.
нет отрицательных, т. е.
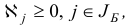
то псевдоплан 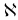 — оптимальный план
— оптимальный план
задачи (2.5). При этом базисный двойственный план 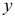 , определяющий псевдоплан
, определяющий псевдоплан  , является решением задачи (2.6).
, является решением задачи (2.6).
Утверждение 2. Пусть среди базисных компонент 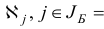
 псевдоплана
псевдоплана 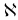 имеется отрицательная компонента
имеется отрицательная компонента 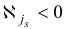 и выполняются неравенства
и выполняются неравенства
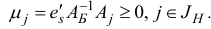
Тогда целевая функция двойственной задачи не ограничена снизу на множестве своих планов, а ограничения прямой задачи несовместны.
Утверждение 3. Пусть базисный двойственный план 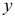 (с базисом
(с базисом 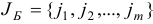 ) является невырожденным. Если среди базисных компонент псевдоплана
) является невырожденным. Если среди базисных компонент псевдоплана 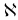 , построенного по
, построенного по 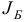 , есть отрицательная компонента
, есть отрицательная компонента 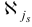 , для которой
, для которой 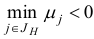 , то можно перейти к новому базисному двойственному плану
, то можно перейти к новому базисному двойственному плану 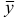 с лучшим значением двойственной целевой функции:
с лучшим значением двойственной целевой функции: 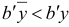 .
.
Новый базисный двойственный план 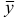 и соответствующий ему базис
и соответствующий ему базис 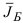 строятся по плану
строятся по плану
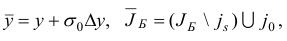
где
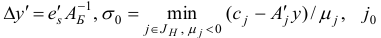
произвольный индекс из множества
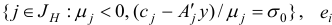
единичный 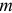 -вектор с единицей на
-вектор с единицей на 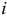 -м месте.
-м месте.
Возможно эта страница вам будет полезна:
| Методы решения задач линейного программирования |
Двойственный симплекс-метод
Метод решения канонической задачи линейного программирования, рассмотренный в разд. 1, впредь будем называть прямым симплекс-методом.
Опишем двойственный симплекс-метод, который является специальным алгоритмом построения оптимального плана задачи линейного программирования (2.5) посредством преобразования планов двойственной задачи (2.6).
Для решения задачи (2.5) двойственным симплекс-методом, кроме исходных данных 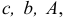 на каждой итерации необходимо знать следующие параметры:
на каждой итерации необходимо знать следующие параметры:
1) текущий базисный двойственный план 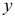 ;
;
2) соответствующий двойственному плану 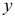 базис
базис
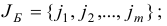
3) 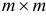 -матрицу
-матрицу 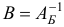 обратную к базисной матрице
обратную к базисной матрице
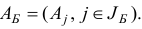
Опишем общую итерацию двойственного симплекс-метода по шагам. Шаг 1. Найдем базисные компоненты псевдоплана 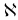 , соответствующего базису
, соответствующего базису
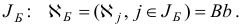
Шаг 2. Если выполняются неравенства
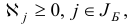
то STOP: вектор
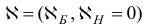
является оптимальным планом задачи (2.5), а вектор 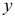 — оптимальным планом задачи (2.6). В противном случае перейдем к шагу 3.
— оптимальным планом задачи (2.6). В противном случае перейдем к шагу 3.
Шаг 3. Среди базисных индексов
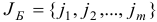
выберем индекс 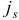 , для которого
, для которого 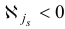 . Подставим
. Подставим 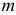 -вектор
-вектор 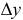 и числа
и числа 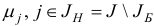 , по правилам
, по правилам
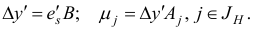
Если 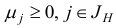 , то STOP: ограничения исходной задачи (2.5) несовместны, а целевая функция двойственной задачи (2.6) не ограничена снизу на множестве ее планов. В противном случае перейдем к шагу 4. Шаг 4. Найдем минимум
, то STOP: ограничения исходной задачи (2.5) несовместны, а целевая функция двойственной задачи (2.6) не ограничена снизу на множестве ее планов. В противном случае перейдем к шагу 4. Шаг 4. Найдем минимум
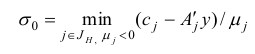
и выберем в качестве индекса 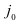 любой элемент из множества
любой элемент из множества
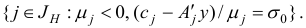
Шаг 5. Построим новый базисный двойственный план 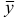 и соответствующий ему базис
и соответствующий ему базис 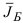 по правилам
по правилам
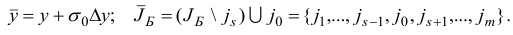
Шаг 6. Вычислим матрицу 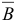 , обратную к новой базисной матрице
, обратную к новой базисной матрице
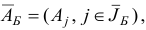
по правилам, описанным на шаге 6 итерации прямого симплекс-метода (см. подразд. 1.4).
Переходим к следующей итерации, исходя из новых значений для базисного двойственного плана 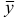 , базиса
, базиса 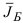 и матрицы
и матрицы 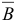 .
.
Замечания. 1. На шаге 3 выбор индекса 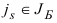 и на шаге 4 выбор индекса
и на шаге 4 выбор индекса 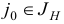 могут оказаться неоднозначным. Как и в прямом симплекс-методе, это может привести к зацикливанию алгоритма. Для предотвращения зацикливания рекомендуется использовать дополнительные правила, аналогичные приведенным в подразд. 1.6. Например, правило Блэнда для двойственного симплекс-метода сводится к следующему: на шаге 3 индекс
могут оказаться неоднозначным. Как и в прямом симплекс-методе, это может привести к зацикливанию алгоритма. Для предотвращения зацикливания рекомендуется использовать дополнительные правила, аналогичные приведенным в подразд. 1.6. Например, правило Блэнда для двойственного симплекс-метода сводится к следующему: на шаге 3 индекс 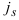 однозначно определяется условием
однозначно определяется условием
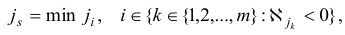
а на шаге 4 индекс 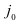 однозначно определяется соотношением
однозначно определяется соотношением
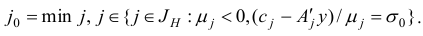
Легко проверить, что если базисный двойственный план 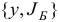 является невырожденным, то для нового базисного плана
является невырожденным, то для нового базисного плана 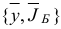 справедливо неравенство
справедливо неравенство 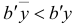 . (В общем случае верно неравенство
. (В общем случае верно неравенство 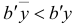 ).
).
Проблема построения начального базисного двойственного плана 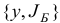 является нетривиальной. Для ее решения по аналогии с разделом 1 можно разработать двухфазный двойственный симплекс-метод.
является нетривиальной. Для ее решения по аналогии с разделом 1 можно разработать двухфазный двойственный симплекс-метод.
Задача №6
Решить задачу ЛП двойственным симплекс-методом
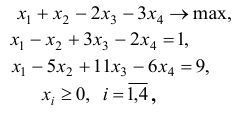
приняв в качестве начального базисного двойственного плана вектор
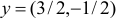
и базисное множество 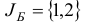 .
.
Решение:
Базису 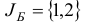 соответствует базисная матрица
соответствует базисная матрица
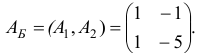
Построим матрицу
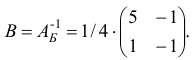
Используя
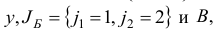
и осуществим первую итерацию.
Шаг 1. Найдем базисные компоненты псевдоплана  , соответствующего базису
, соответствующего базису 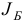 :
:
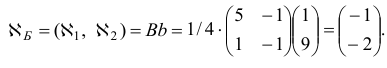
Шаг 2. Условие
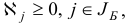
не выполняется, следовательно, переходим к шагу 3.
Шаг 3. В качестве индекса
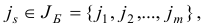
для которого 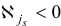 , выберем индекс
, выберем индекс 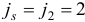 . Подсчитаем вектор
. Подсчитаем вектор 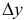 и числа
и числа 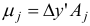 ,
, 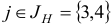 :
:
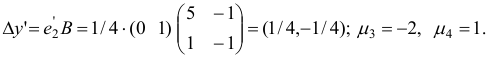
Поскольку среди чисел 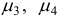 есть отрицательные, то переходим к шагу 4.
есть отрицательные, то переходим к шагу 4.
Шаг 4. Найдем минимум
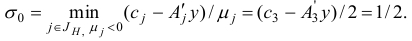
В данном примере в качестве индекса 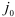 можно выбрать только индекс
можно выбрать только индекс 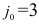 .
.
Шаг 5. Построим новый базисный двойственный план 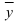 и соответствующий ему базис
и соответствующий ему базис 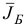 по правилам
по правилам
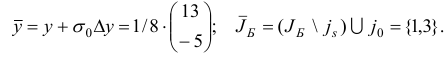
Шаг 6. По правилам, описанным на шаге 6 прямого симплекс-метода, вычислим матрицу
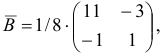
обратную к новой базисной матрице
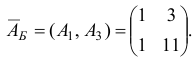
Переходим ко второй итерации, исходя из новых значений для базисного двойственного плана 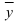 , базиса
, базиса
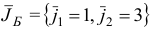
и матрицы 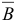 .
.
Осуществим вторую итерацию.
Шаг 1. Найдем базисные компоненты псевдоплана 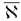 , соответствующего базису
, соответствующего базису 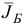 :
:
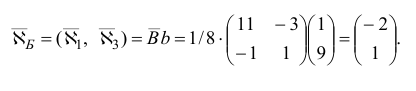
Шаг 2. Поскольку среди компонент
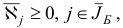
есть отрицательные, то переходим к шагу 3.
Шаг 3. На данной итерации в качестве индекса 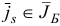 , для которого
, для которого 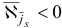 , можно выбрать только индекс
, можно выбрать только индекс 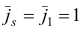 . Найдем
. Найдем
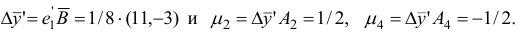
Поскольку среди чисел 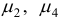 есть отрицательные, то переходим к шагу 4.
есть отрицательные, то переходим к шагу 4.
Шаг 4. Найдем
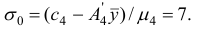
В качестве индекса 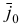 можно выбрать только индекс
можно выбрать только индекс 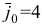 .
.
Шаг 5. Построим новый базисный двойственный план 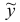 и соответствующий ему базис
и соответствующий ему базис 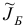 :
:
Шаг 6. Вычислим матрицу
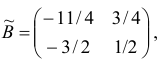
обратную к новой базисной
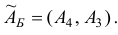
Переходим к третьей итерации, исходя из новых значений для базисного двойственного плана 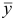 , базиса
, базиса 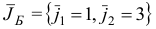 и матрицы
и матрицы 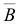 . Опишем третью итерацию.
. Опишем третью итерацию.
Шаг 1. Найдем базисные компоненты псевдоплана 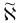 , соответствующего базису
, соответствующего базису 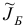 :
:
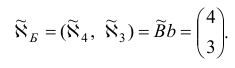
Шаг 2. Все компоненты 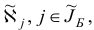 положительны, следовательно, вектор
положительны, следовательно, вектор
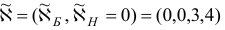
является оптимальным планом рассматриваемой задачи, а вектор 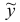 — ее оптимальным двойственным планом. Задача решена.
— ее оптимальным двойственным планом. Задача решена.
Возможно эти страницы вам будут полезны:
- Графическое решение задач линейного программирования
- Графический метод решения задач линейного программирования
- Заказать работу по линейному программированию
- Помощь по линейному программированию
- Контрольная работа по линейному программированию
- Линейное программирование в Excel
- Курсовая работа по линейному программированию
