Математическое программирование задачи с решением

Прежде чем изучать готовые решения задач по математическому программированию, нужно знать теорию, поэтому для вас я подготовила краткую теорию по предмету «математическое программирование», после которой подробно решены задачи.

Эта страница подготовлена для школьников и студентов.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Математическое программирование

Математическое программирование – раздел высшей математики, разрабатывающий теорию и численные методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.

Жордановы исключения

Пусть дана система линейных уравнений

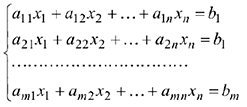
В матрице 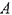этой системы выберем отличный от нуля элемент . Этот элемент называется разрешающим элементом, 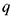— й столбец матрицы 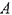— разрешающим столбцом, а 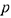— я строка — разрешающей строкой. Рассмотрим новую систему уравнений

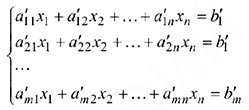
с матрицей 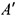коэффициенты и свободные члены этой системы определяются по формулам

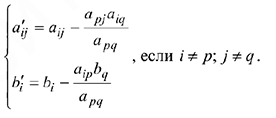
Если же 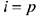. го принимаем 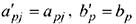. Таким образом, 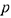— е уравнения в системах (1.1) и (1.2) одинаковы, а коэффициенты при 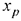во всех уравнениях системы (1.2), кроме 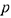— го, равны нулю.

Системы (1.1) и (1.2) одновременно совместны или несовместны. В случае совместности эти системы равносильны (их решения совпадают).

Для определения элемента 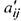матрицы 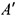применяется правило прямоугольника

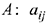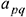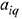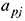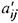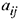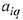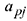Рассмотрим четыре элемента матрицы (элемент, подлежащий преобразованию), (разрешающий элемент) и элементы и . Для нахождения элемента следует из элемента вычесть произведение элементов и расположенных в противоположных вершинах прямоугольника, делённое на разрешающий элемент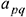

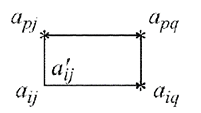
Аналогичным образом можно преобразовать систему (1.2), приняв за разрешающий элемент матрицы 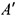элемент 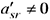, причём .

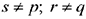После этого преобразования все коэффициенты при 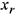, кроме 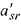, обратятся в нуль. Полученная система может быть снова преобразована и т.д.

Возможно эта страница вам будет полезна:

Предмет математическое программирование

Задача №1.1.

Найти решение системы:

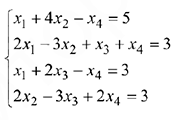
Систему решить методом Жордано-Гаусса: 1) аналитически; 2) с помощью MS Excel.

Решение:

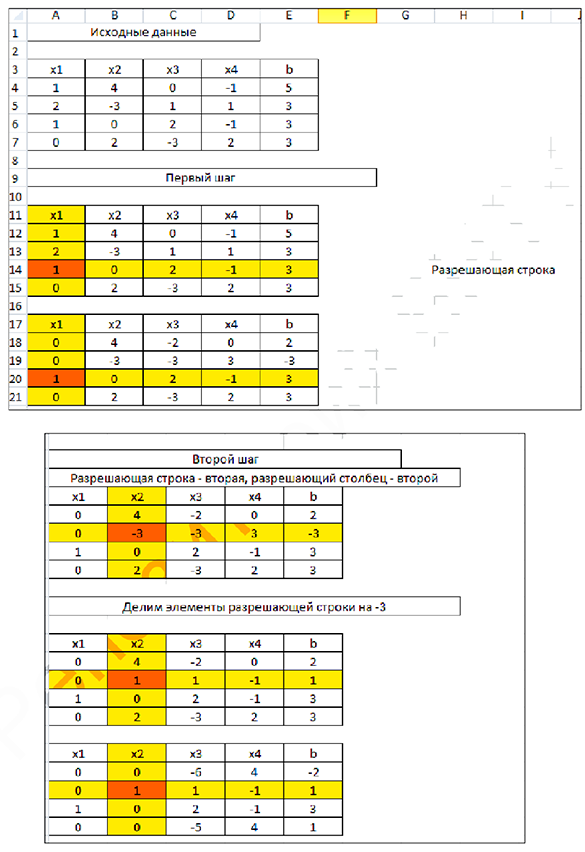
Запишем систему в виде жордановой таблицы.

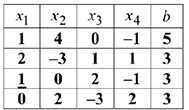
1 шаг. Разрешающий столбец — 1; разрешающая строка — 3; разрешающий элемент 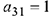. Применим правило прямоугольника.

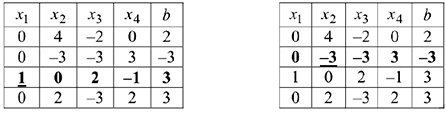
2 шаг. Делим элементы разрешающей строки па -3 и опять применяем правило прямоугольника:

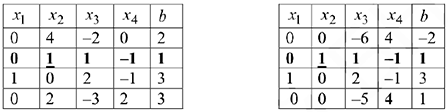
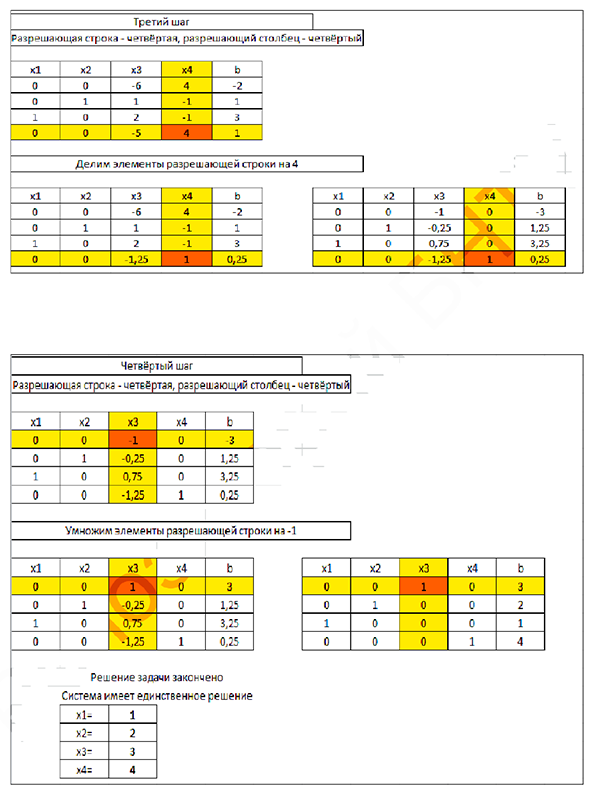
3 шаг. В качестве разрешающего элемента выбираем 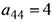. Делим элементы четвёртой строки на 4 и проводим ещё один шаг жордановых исключений:

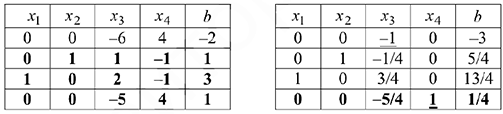
4 шаг. Умножаем первую (разрешающую) строку на -1. Разрешающий столбец — третий.

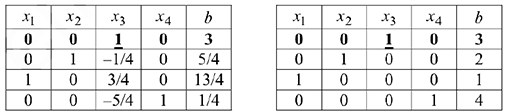
Система имеет единственное решение

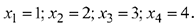
Используем для решения системы MS Excel:

Задача №1. 2.

Решить систему уравнений.

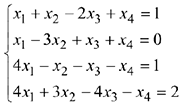
Систему решить методом Жордано-Гаусса с помощью MS Excel.

Решение:

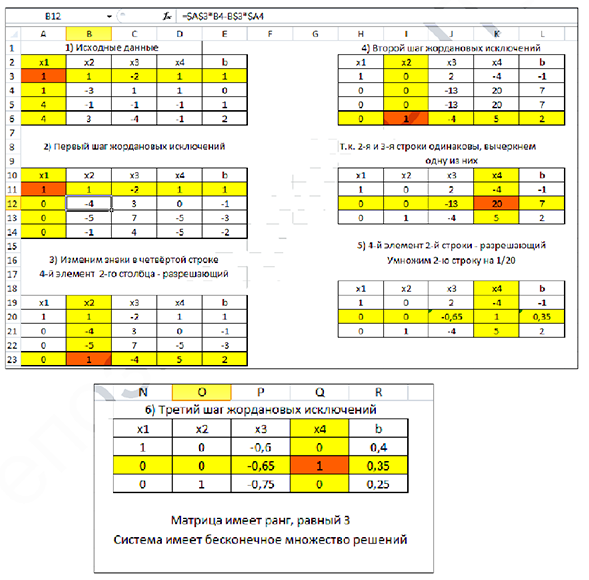
Пусть

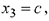
тогда

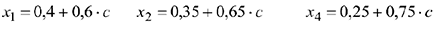
Возможно эта страница вам будет полезна:

Примеры решения задач по математическому программированию

Постановка задачи математического программировании

Рассмотрим оптимизационные задачи, решаемые методами линейного программирования (ЛП), в которых оптимизируемая функция 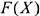является линейной, а ограничения 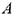задаются линейными неравенствами. Ограничения задают выпуклые линейные многогранники в конечном линейном пространстве. Целевые функции также линейны.

Задача линейного программирования (ЗЛП) записывается следующим образом: найти переменные 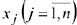, при которых целевая функция

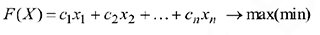
была бы максимальной (минимальной), не нарушая следующих условий:

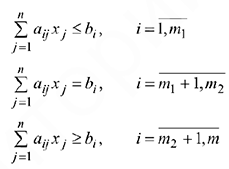
Все три случая можно привести к так называемой канонической форме, введя дополнительные переменные

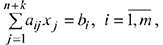
где 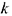— количество дополнительных переменных и условие неотрицательности искомых переменных .

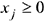В результате решения задачи находится некий план (программа) работы некоторого предприятия. Отсюда и появилось слово «программирование». Слово линейное указывает на линейный характер зависимости, как в целевой функции, так и в системе ограничений. Задача обязательно носит экстремальный характер, т.е. состоит в отыскании максимума или минимума (экстремума) целевой функции. Допустимым решением (планом) задачи линейного программирования называется любой 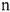-мерный вектор 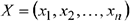удовлетворяющий системе ограничений и условиям неотрицательности. Множество всех допустимых решений задачи образуют область допустимых решений (сокращенно ОДР).

Элементы линейной алгебры и геометрии выпуклых множеств

Система 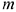линейных уравнений с 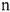переменными имеет вид

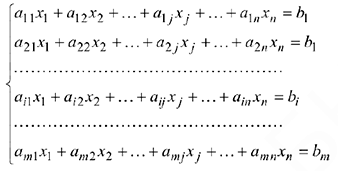
В задачах линейного программирования представляют интерес системы, в которых максимальное число независимых уравнений системы меньше числа переменных, т.е. .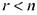

Будем полагать, что в системе (2.1) все 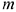уравнений системы независимы, т.е. 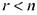и соответственно .

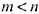Любые 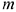переменных системы 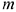линейных уравнений с 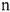переменными (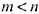) называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные 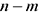переменных называются неосновными (или свободными).

Среди бесконечного множества решений системы выделяют так называемые базисные решения.

Базисным решением системы 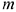линейных уравнений с 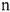переменными называется решение, в котором все 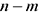неосновных переменных равны нулю.

В задачах линейного программирования особый интерес представляют допустимые базисные решения, или, как их еще называют, опорные планы. Число базисных решений является конечным, так как оно равно числу групп основных переменных, не превосходящему 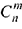. Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным.

Выпуклые множества точек:

В школьном курсе математики выпуклыми назывались многоугольники, целиком расположенные по одну сторону от прямых, на которых лежат их стороны.

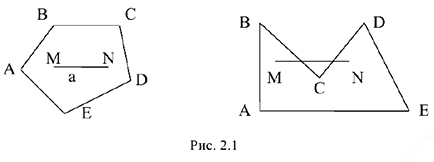
Например, многоугольник на рис. 2.1, а — выпуклый, а многоугольник на рис. 2.1, б не является выпуклым (он расположен по обе стороны от прямой ).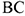

Общим определяющим свойством, которое отличает выпуклый многоугольник от невыпуклого, является то, что если взять любые две его точки и соединить их отрезком, то весь отрезок будет принадлежать этому многоугольнику. Это свойство может быть принято за определение выпуклого множества точек.

Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки.

Выпуклые множества обладают важным свойством, которое устанавливается следующей теоремой.

Теорема 2.1. Пересечение (общая часть) любого числа выпуклых множеств есть выпуклое множество.

Среди точек выпуклого множестваможно выделить внутренние, граничные и угловые точки. Точка множества называется внутренней, если в некоторой ее окрестности содержатся точки только данного множества. Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему. Точка множества называется угловой (или крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.

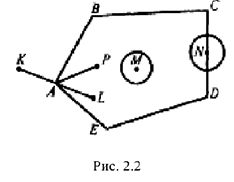
На рис. 2.2 приведены примеры различных точек многоугольника: внутренней (точки 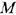), граничной (точка 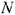) и угловых (точки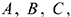 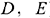). Точка 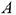— угловая, так как для любого отрезка, целиком принадлежащего многоугольнику, например, отрезка 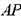, она не является внутренней; точка 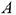— внутренняя для отрезка 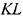, но этот отрезок не принадлежит целиком многоугольнику.

Множество точек называется замкнутым, если включает все свои граничные точки. Множество точек называется ограниченным, если существует шар (круг) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество; в противном случае множество называется неограниченным.

Если фигура ограничена только прямыми или их отрезками, то число ее угловых точек конечно; в случае криволииейпости границ фигура содержит бесконечно много угловых точек, что позволяет сделать следующее определение.

Выпуклое замкнутое множество точек пространства (плоскости), имеющее конечное число угловых точек, называется выпуклым многогранником (,многоугольником•), если оно ограниченное, и выпуклой многогранной (многоугольной) областью, если оно неограниченное.

Множество всех точек 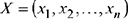образует 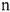-мерное точечное (векторное) пространство. При 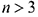точки и фигуры «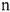-мерного пространства» не имеют реального геометрического смысла и все исследования объектов этого пространства необходимо проводить в аналитической форме.

Тем не менее оказывается целесообразным и в этом случае использовать геометрические понятия для облегчения представлений об объектах — мерного пространства.

Геометрический смысл решений неравенств, уравнений и их систем

Теорема 2.2. Множество решений неравенства с двумя переменными

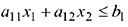
является одной из двух полуплоскостей, на которые вся плоскость делится прямой

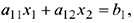
включая и эту прямую, а другая полуплоскость с той же прямой есть множество решений неравенства

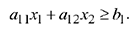
Учитывая, что множество точек, удовлетворяющих уравнению

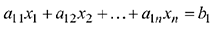
при 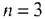, является плоскостью, а при 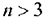— ее обобщением в 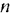-мерном пространстве — гиперплоскостью, теорему 2.2 можно распространить на случай трех и более переменных.

Теорема 2.3. Множество всех решений линейного неравенства с 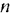переменными

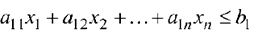
является одним из полупространств, на которые все пространство делится плоскостью или гиперплоскостью (2.2), включая и эту плоскость (гиперплоскость).

Рассмотрим множество решений систем неравенств:

Теорема 2.4. Множество решений совместной системы 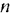линейных неравенств с двумя переменными

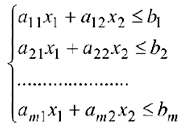
является выпуклым многоугольником (или выпуклой многоугольной областью).

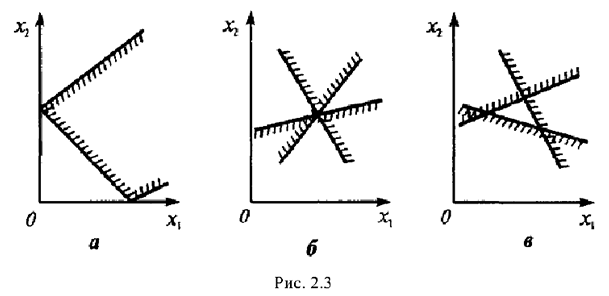
При построении областей решений систем неравенств могут встретиться и другие случаи: множество решений — выпуклая многоугольная область (рис. 2.3, а); одна точка (рис. 2.3, б); пустое множество, когда система неравенств несовместна (рис. 2.3, в).

Теорема 2.5. Множество решений совместной системы от линейных неравенств с 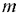переменными является выпуклым многогранником (выпуклой многогранной областью) в 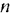-мерном пространстве.

Рассмотрим множество допустимых решений системы 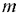линейных уравнений с 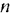переменными.

Теорема 2.6. Множество всех допустимых решений совместной системы 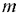линейных уравнений с 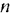переменными (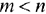) является выпуклым многогранником (выпуклой многогранной областью) в 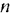-мерном пространстве.

Возможно эта страница вам будет полезна:

Заказать работу по математическому программированию

Графический метод решения ЗЛП

Методы решения задач линейного программирования относятся к вычислительной математике. Задачу линейного программрования можно решать аналитическими и графическими методами. Аналитические методы, которые представляют собой последовательность вычислений по некоторым правилам, являются основой для решения задачи на компьютере. Их единственный недостаток заключается в том, что в отличие от графических методов, они совершенно не наглядны. Графические же методы достаточно наглядны, но они пригодны лишь для решения таких задач, что даёт возможность представлять задачу на плоскости.

Рассмотрим задачу линейного программирования с двумя переменными

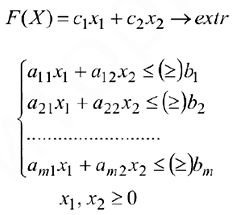
Такая задача может быть решена графически (геометрически) ввиду того, что в этом случае легко строить ОДР (область допустимых решений).

Алгоритм графического решения задачи линейного программирования состоит в выполнении следующих действий.

1) Построить ОДР.

2) Построить вектор нормали 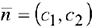целевой функции (он указывает па направление возрастания целевой функции).

3) Построить нижнюю и верхнюю опорные прямые 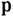и 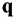, т. е. крайние линии уровня целевой функции, имеющие общие точки с ОДР.

4) Определить координаты экстремальных точек .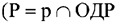

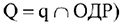Примечания.

1) Если ОДР — пустое множество, то задача не имеет решения ввиду несовместности системы ограничений.

2) Если ОДР неограничена по направлению вектора 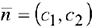, то сама целевая функция неограничена сверху в этой области, и принимаем 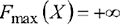. Если ОДР неограничена в направлении, противоположном 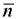, то принимаем .

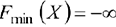Графически может быть решена также задача линейного программирования, заданная в канонической форме, при условии 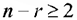( 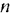— число переменных, 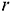— ранг системы уравнений). Для этого задачу надо привести к симметрическому виду.

Возможно эта страница вам будет полезна:

Помощь по математическому программированию

Задача №2.1.

Найти все базисные решения системы уравнений.

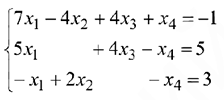
Решение:

Запишем систему в таблицу. Жордановы исключения будем выполнять в пакете MS Excel (Таблицы 2.1 — 2.4).

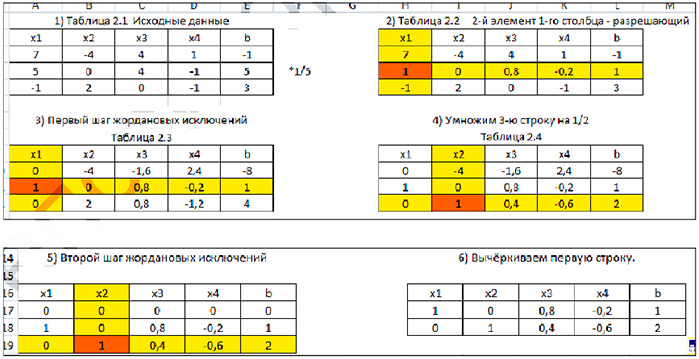
Эквивалентная система:

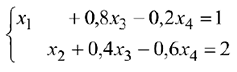
Система приведена к единичному базису, и переменные 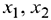составляют один из базисов системы переменных 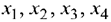. Поэтому при нулевых значениях свободных переменных 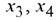получаем одно из базисных решений

Б, = (1,2, 0, 0).

В данном случае 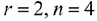, поэтому всего базисных решений может 2 4!

быть не более 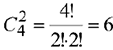. Другими базисами могут оказаться следующие группы переменных:

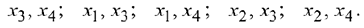
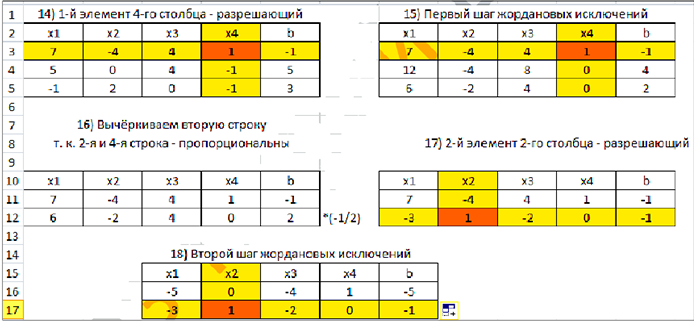
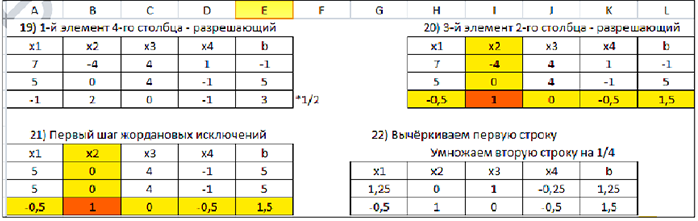
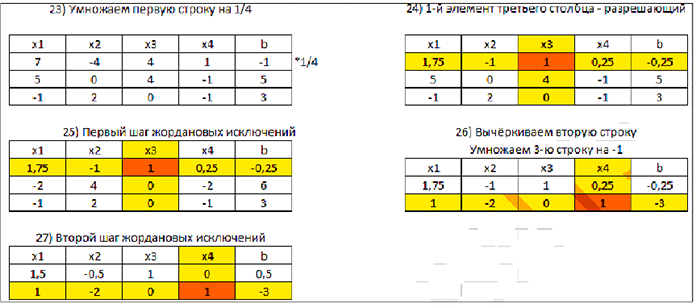
Для того чтобы найти второе базисное решение 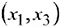, вернемся к таблице 2.3. Вычеркнем из неё первую строку (первая и третья строки пропорциональны) и примем за разрешающий третий столбец. Получим таблицы 2.3 — 2.6.

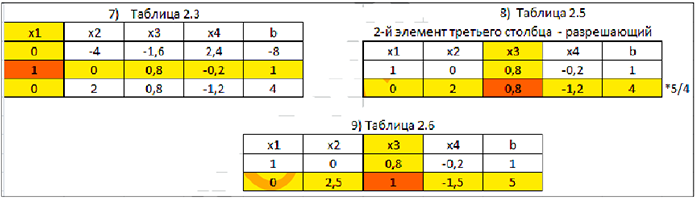
Сделав шаг жордановых исключений, перейдём к базису 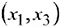и при 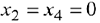(таблица 2.7) получим ещё одно базисное решение :

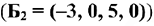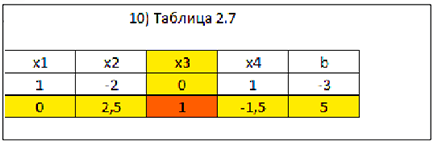
Преобразовывая последовательно шагами жордановых исключений таблицы 2.5, 2.1 получим другие базисные решения:

Базисные переменные 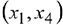. Свободные переменные 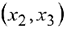. Базисное решение

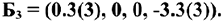
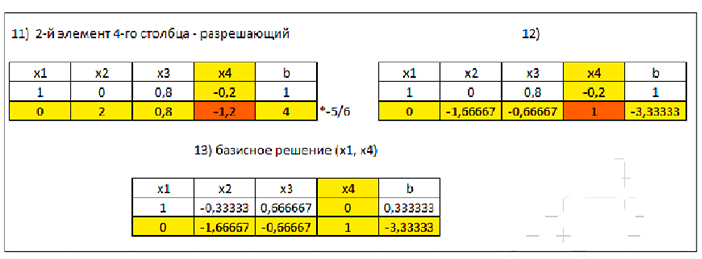
Базисные переменные 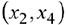. Свободные переменные 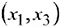. Базисное решение

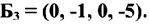
Базисные переменные 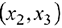. Свободные переменные 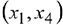. Базисное решение

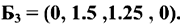
Базисные переменные 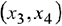. Свободные переменные 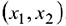. Базисное решение

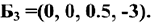
Задача №2.2.

Записать в форме стандартной задачи линейного программирования следующую задачу:

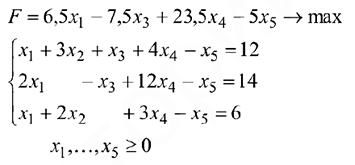
Решение:

Приведём систему ограничительных уравнений к разрешённой форме, выделяя некоторый базис переменных. Затем, опустив базисные переменные, перейдём к эквивалентной системе неравенств. Для завершения преобразований останется выразить целевую функцию через переменные, вошедшие в полученную систему неравенств.

Эти преобразования удобнее проводить одновременно, приписав к жордановой таблице снизу строку для целевой функции (—строку). В процессе жордановых исключений эту строку не следует делать разрешающей, но преобразовывать её элементы нужно по обычным правилам. В результате целевая функция, как и базисные переменные, окажется выраженной через свободные переменные.

В условиях данной задачи разрешающие элементы можно выбрать произвольно

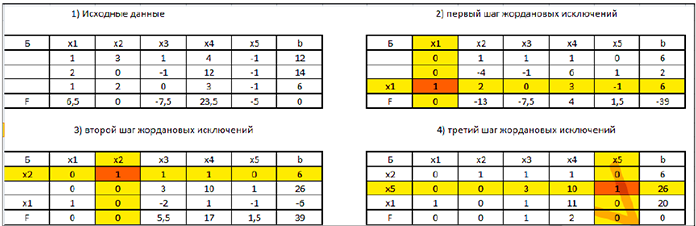
Учитывая неотрицательность базисных переменных 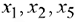в последней таблице, опускаем их и приходим к эквивалентной системе неравенств. а вместе с тем и к симметричной форме записи задачи:

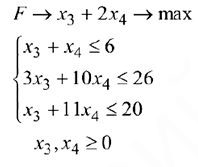
Задача №2.3.

Решить графически следующую задачу математического программирования:

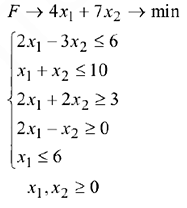
Решение:

а) Область допустимых решений, которую обозначим буквой 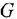, построим следующим образом. Построим прямые с уравнениями:

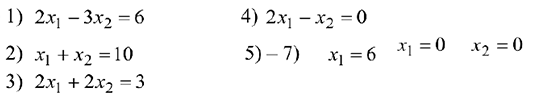
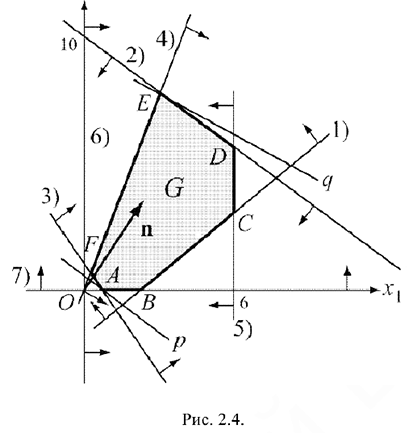
Прямые пронумерованы. Помер прямой имеется также на рисунке 2.4.

б) Каждое неравенство, фигурирующее в системе ограничений, определяет полуплоскость, причем эта полуплоскость содержит точку, координаты которой удовлетворяют соответствующему строгому неравенству.

Первые два и четвертое неравенства системы ограничений удовлетворяются координатами точки .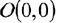

Поэтому три полуплоскости содержат начало координат системы .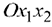

На соответствующую полуплоскость указывают стрелки, идущие от каждой прямой. Жирной линией выделим границу ОДР выпуклый шестиугольник 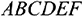. Последние неравенства 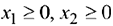, означающие неотрицательность переменных задачи, определяют первую четверть плоскости .

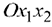в) Строим теперь нормальный вектор целевой функции 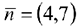. Его направление указывает направление возрастания целевой функции .

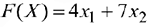Прямая с уравнением 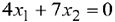представляет собой «нулевую» линию уровня функции 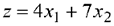. Эта прямая проходит через начало координат и перпендикулярна нормальному вектору 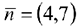Передвигаем эту прямую параллельно себе, или перпендикулярно 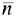, и фиксируем два ее крайних положения.

Эти крайние прямые, которые обозначим буквам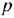и и 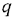, должны иметь с границей 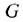либо общую вершину, либо общий отрезок, причем направление от 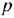к 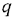совпадает с направлением 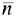. В нашем случае 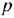проходит через точку 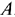, a 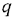— через точку 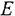. Эти прямые называются соответственно нижней и верхней опорными прямыми для .

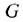г) Определим координаты точек 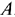и 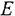. На чертеже видно, что точка 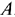лежит на прямых 3) и 7), а 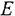— на 2) и 4). Именно поэтому пронумерованы уравнения прямых и их изображения. Теперь легко составить системы уравнений для определения координат этих точек. Запишем это так:

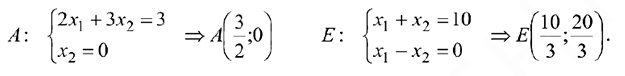
Вычислим значения целевой функции в точках 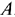и :

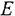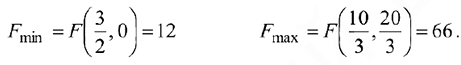
Возможно эта страница вам будет полезна:

Задачи математического программирования

Симплекс-метод. Краткие теоретические сведении

Симплекс-метод. Максимум или минимум целевой функции может быть достигнут в одной из угловых точек области допустимых планов.

Сделанный вывод на первый взгляд позволяет предположить простой метод решения задач линейного программирования: надо просто «перебрать» все угловые точки области допустимых планов, в каждой из них вычислить значение целевой функции и выбрать ту угловую точку, где целевая функция оптимальна.

Однако количество угловых точек области допустимых планов растет очень резко с ростом числа переменных и особенно числа ограничений. Число перебираемых вершин можно сократить, если производить перебор не беспорядочно, а с учетом изменений целевой функции, т.е. добиваясь того, чтобы каждое следующее решение было «лучше» (или, по крайней мере, «не хуже»), чем предыдущее (было ближе к оптимальному решению).

Эта идея легла в основу универсального метода решения задач линейного программирования — симплекс-метода.

Симплекс-метод — один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования. Он был предложен американцем Г. Данцигом в 1951 г. Симплекс-метод состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум.

Задача №3.1.

Найти какой-либо опорный план задачи (математически).

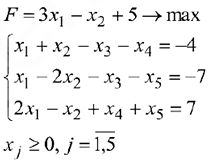
Решить задачу в Excel, используя «Поиск решения».

Решение:

Задача записана в канонической форме, но 2 свободных члена отрицательны, поэтому, прежде чем записать задачу в форме таблицы, умножим первое и второе уравнение на (-1).

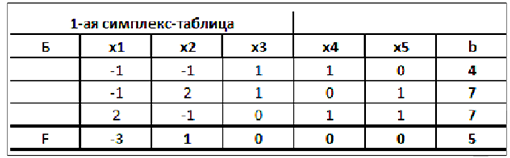
Для первого шага жорданова исключения возьмём разрешающим, например, четвёртый столбец — в нём есть положительные элементы. Разрешающая строка определится по минимальному из отношений: 4/1 и 7/1.

В данном случае

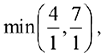
что соответствует первой строке, которая и будет разрешающей.

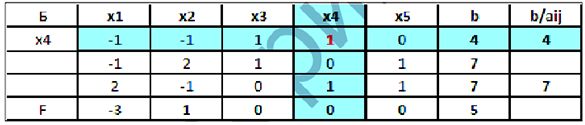
Сделаем ещё 2 шага жордановых исключений, получим:

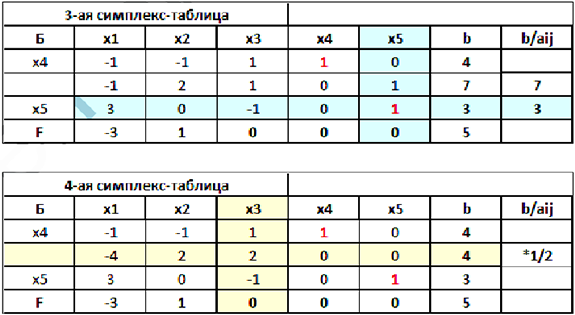
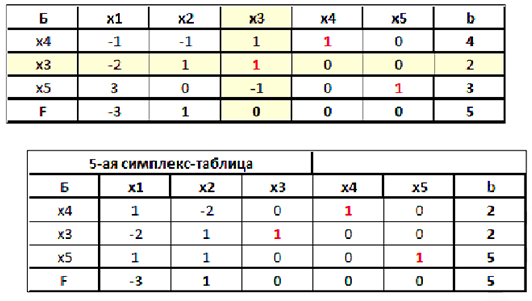
Базис выделен. Ему соответствует начальный опорный план

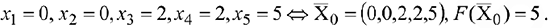
Был найден опорный план в базисе 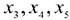. Если исходную таблицу преобразовать с другими разрешающими элементами, то получится другой базис — следовательно, и другой опорный план.

Решение задачи в процедуре EXCEL «Поиск решения».

1) Ввод данных в таблицу EXCEL (рис. 3.1).

Для переменных задачи отведены ячейки B3:F3. Эти ячейки называются рабочими или изменяемыми ячейками.

В изменяемые ячейки ничего не заносится и в результате решения задачи в этих ячейках будет оптимальные значения переменных.

В ячейку G4 вводится формула для вычисления целевой функции задачи 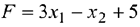(рис. 3.2):

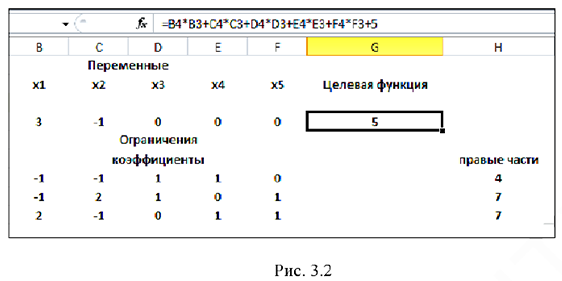
В ячейку G7 вводится формула для вычисления ограничения 1: 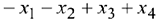, в ячейку G8 вводится формула для вычисления ограничения 2: 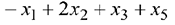а в ячейку G9 — вычисления ограничения 3: 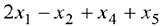. Обе формулы вводятся с помощью функции СУММПРОИЗВ0:

Окончательно после ввода формул и данных экран имеет вид (рис. 3.4):

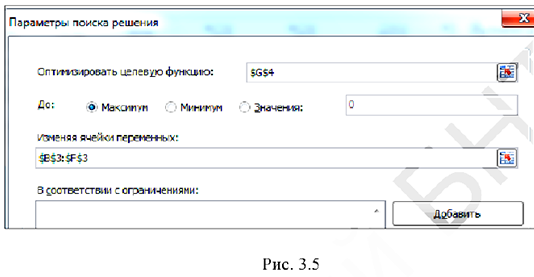
2) Работа в окне «Поиск решения»»

В меню «Данные» выбираем процедуру «Поиск решения» В появившемся окне (рис. 3.5) нужно установить адрес целевой ячейки G4, значение целевой ячейки: максимальное, адреса изменяемых ячеек B3:F3.

Чтобы ввести ограничения задачи, нажать кнопку «Добавить». В появившемся диалоговом (рис. 3.6) окне слева ввести адрес G7 (ограничение 1), затем выбрать знак <= и в правой — адрес ячейки Н7.

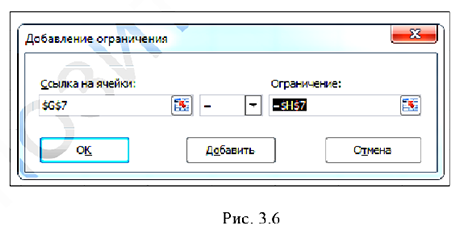
После ввода нажать кнопку «Добавить» и аналогично ввести второе и третье ограничение. Снова нажать кнопку <<Добавить» и ввести ограничение: В3:3 >-0 (соответствующее ограничению ).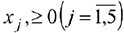

После ввода последнего ограничения нажать ОК. В опции «Выбрать метод решения» выбрать «Поиск решения линейных задач симплекс-методом». Окно «Поиска решений» будет иметь вид (рис. 3.7):

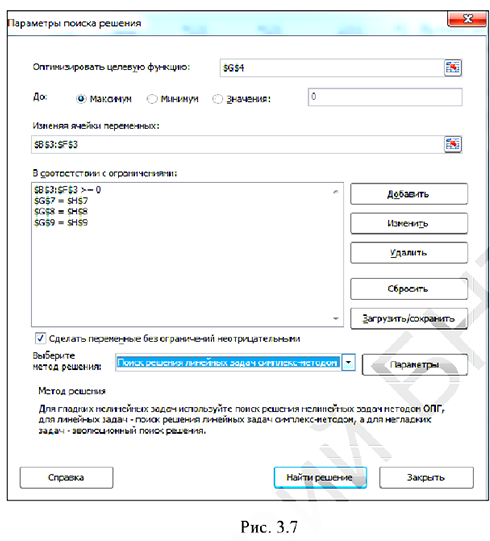
Для решения задачи в окне «Поиск решения» нажать кнопку «Найти решение». Если решение найдено появляется окно (рис. 3.8):

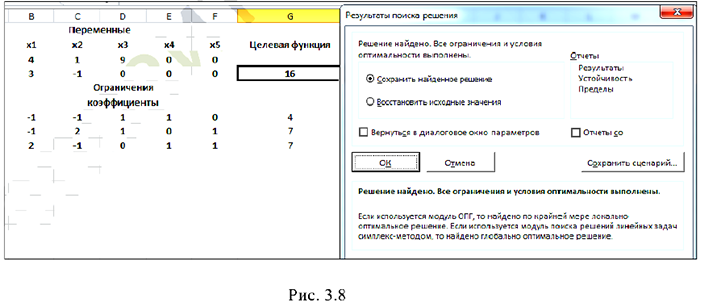
Оптимальное решение задачи линейного программирования:

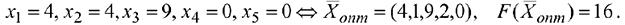
Был найден оптимальный план в базисе

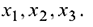
Различные технико-экономические и экономические задачи производственного менеджмента, от оптимальной загрузки станка и раскройки стального листа или полотна ткани

до анализа межотраслевого баланса и оценки темпов роста экономики страны в целом, приводят к необходимости решения тех или иных задач линейного программирования.

Возможно эта страница вам будет полезна:

Задача линейного программирования

Задача №3.2.

Задача распределения ресурсов.

Если финансы, оборудование, сырьё и даже людей полагать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Достаточно часто математической моделью таких задач является задача линейного программирования.

Рассмотрим следующий пример.

Требуется определить, в каком количестве надо выпускать продукцию четырёх типов Прод1, Прод2, ПродЗ, Прод4, для изготовления которой требуются ресурсы трёх видов: трудовые, сырьё, финансы. Количество ресурсов каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице 2. Там же приведено наличие располагаемого ресурса.

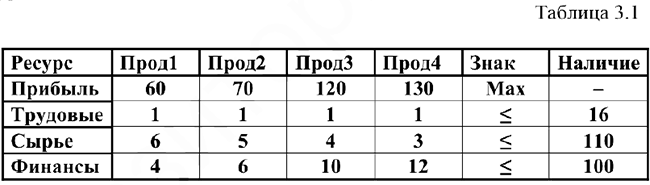
Составить математическую модель, решить задачу симплекс-методом, применяя процедуру Excel «Поиск решения».

Решение:

Введём следующие обозначения:

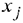— количество выпускаемой продукции 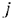— го типа, 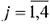; 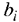j — количество располагаемого ресурса 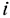— го вида, 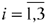; 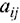— норма расхода 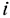— го ресурса для выпуска единицы продукции 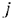— го типа;

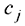— прибыль, получаемая от реализации единицы продукции 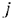— го типа.

Как видно из таблицы 2, для выпуска единицы Прод1 требуется 6 единиц сырья, значит, для выпуска всей продукции Прод1 требуется 6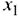 единиц сырья, где 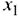— количество выпускаемой продукции Прод1. С учётом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид:

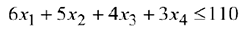
В этом ограничении левая часть равна величине необходимого ресурса, а правая показывает количество имеющегося ресурса.

Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид:

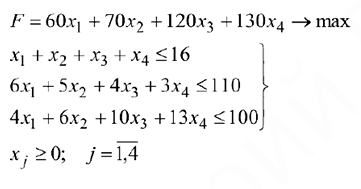
Решение задачи в пакете EXCEL с поиощью «Поиск решения». 1) Ввод данных в таблицу EXCEL (рис. 3.9).

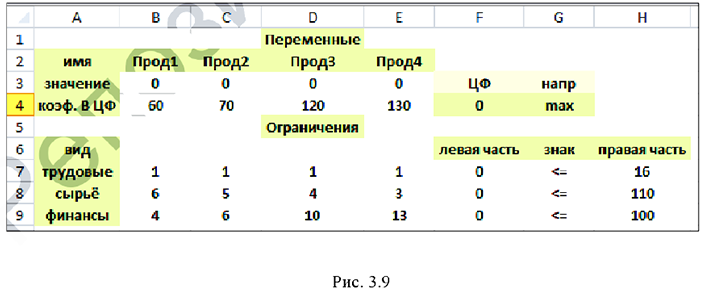
2) Работа в окне «Поиск решения»»

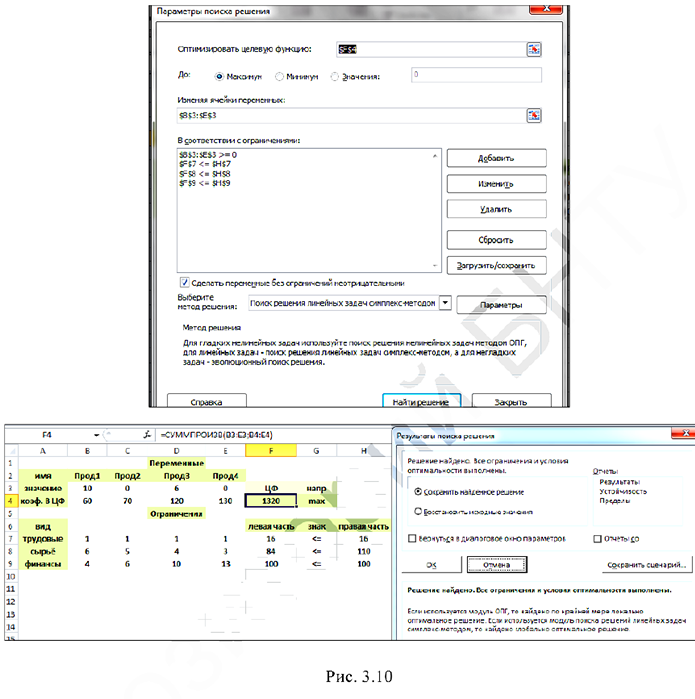
На рис. 3.10 видно, что в оптимальном решении ПроЫ =ВЗ = 10 Прод2 = СЗ = 0 ПродЗ = D3 = 6 Прод4 = ЕЗ = 0.

При этом максимальная прибыль будет составлять F4 = 1320, а количество использованных ресурсов равно

трудовых — F7 = 16 сырья = F8 = 84 финансов = F9 = 100 Анализ оптимального решения.

Анализ оптимального решения начинается после успешного решения задачи, когда на экране появляется диалоговое окно Результат поиска решения. Решение найдено (рис. 3.10). С помощью этого диалогового окна можно вызвать отчёты трёх типов: •Результаты

•Устойчивость • Пределы.

Вызов отчётов анализа.

Начнём с отчёта по результатам. Выделяем вызываемый отчёт и жмём на ОК (рис. 3.1 1)

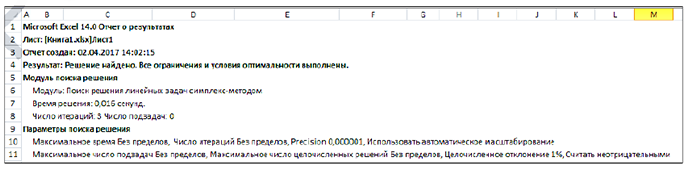
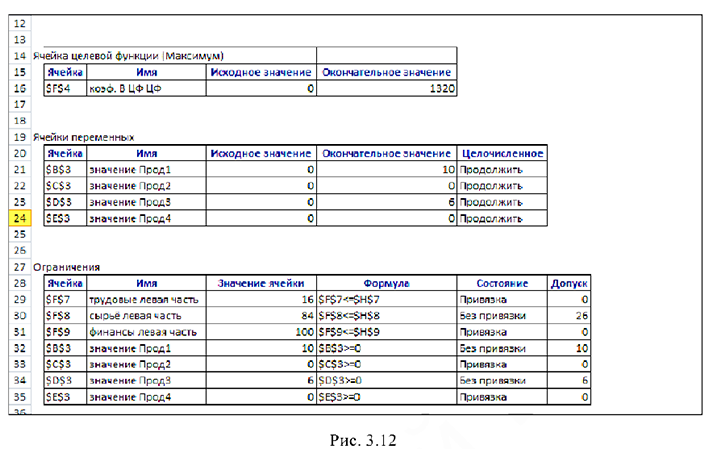
На экране: вызванный отчёт на новом листе, на ярлыке которого указано название отчёта (рис. 3.12).

Отчёт состоит из трёх таблиц.

• Таблица 1 приводит сведения о целевой функции.

•Таблица 2 приводит значения искомых переменных, полученные в результате решения задачи.

•Таблица 3 показывает результаты оптимального решения для ограничений и граничных условий.

Для Ограничений в графе Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения; в графе Значение ячейки приведены величины использованного ресурса; в графе Допуск показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние указывается Привязка; при неполном использовании ресурса в этой графе указывается Без привязки.

Для Граничных условий приводятся аналогичные величины с той лишь разницей, что вместо величины неиспользованного ресурса показана разность между значением переменой в найденном оптимальном решении и заданным для неё граничным условием.

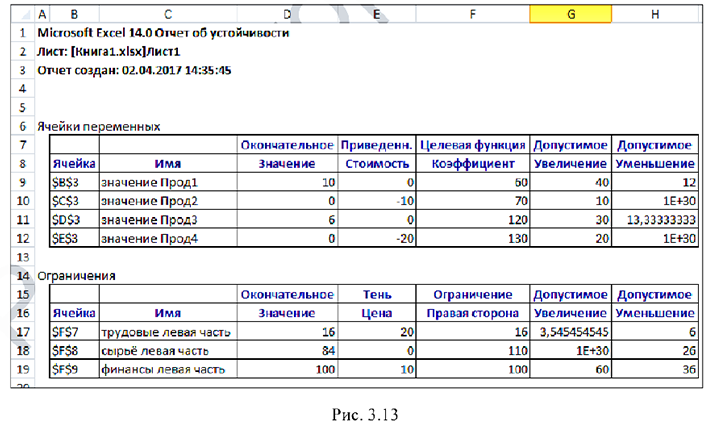
Отчёт по устойчивости (рис. 3.13) состоит из двух таблиц.

В таблице 1 приводятся следующие значения для переменных:

•результат решения задачи;

• приведенная стоимость, т.е. дополнительные двойственные переменные, которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение;

• коэффициенты целевой функции;

• предельные значения приращения коэффициентов 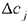целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение.

В таблице 2 приводятся аналогичные значения для ограничений:

• величина использованных ресурсов;

•теневая цена, т.е. двойственные оценки 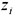, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;

•значения приращения ресурсов 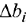при которых сохраняется оптимальный объём переменных, входящих в оптимальное решение.
Отчёт по пределам приведён на рис. 3.14.

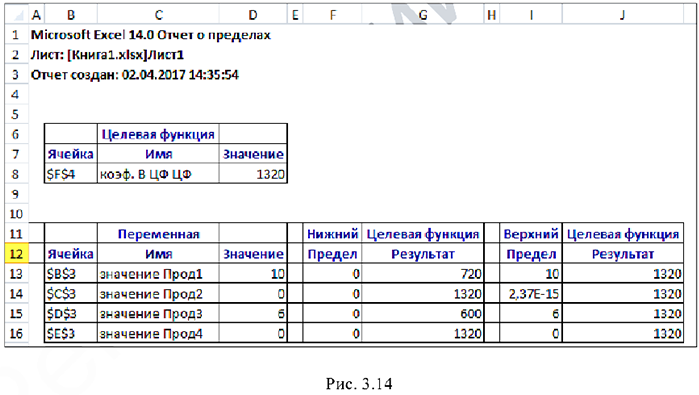
В нём показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения:

• приводятся значения 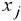в оптимальном решении;

• приводятся нижние пределы изменения значений .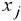

Кроме этого, в отчёте указаны значения целевой функции при выпуске данного типа продукции на нижнем пределе. Так, при значении 720 видно, что

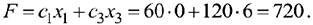
Далее приводятся верхние пределы изменения 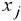— и значения целевой функции при выпуске продукции, вошедшей в оптимальное решение на верхних пределах.

Поэтому везде

Решение задачи математического программирования в microsoft excel

Постановка задачи:

Предприятие выпускает продукцию двух типов 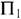и 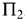. Запас сырья и нормы расхода сырья на условную единицу продукции каждого типа даны в таблице.

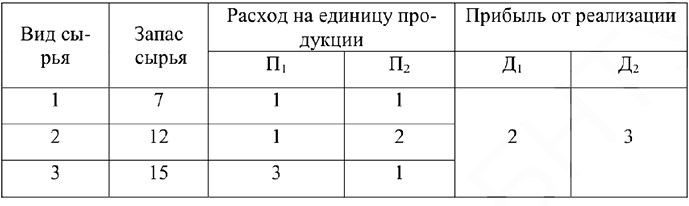
Прибыль от реализации продукции типа 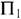составляет 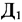денежных единиц, а прибыль от реализации продукции типа 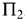составляет 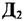денежных единиц. Как следует спланировать выпуск продукции, чтобы прибыль была наибольшей?

Решение данной задачи графическим методом в табличном редакторе Microsoft Excel

Математическая модель и исходные данные задачи — на рисунке 2.3.

Для построения области допустимых решений, 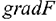и линии уровня необходимо:

1) Выделить данные в области (например, C17:D29), и на вкладке «Вставка» выбрать: «Точечная». Затем после построения первой линии из области допустимых решений, щёлкнуть правой клавишей мыши на области диаграммы и выбрать «Выбрать данные».

2) Щёлкнуть мышью по «Ряд 1» и выбрать кнопку «Изменить». В поле имя ряда записать уравнение построенной прямой (см. рис. 4.1)

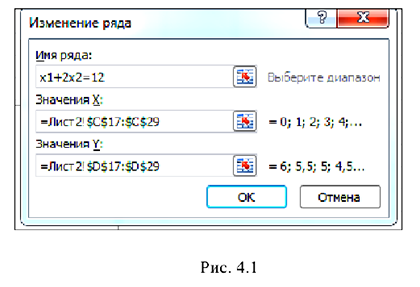
3) Нажать кнопку «Добавить» и выбрать исходные данные для построения второго графика (см. рис. 4.2)

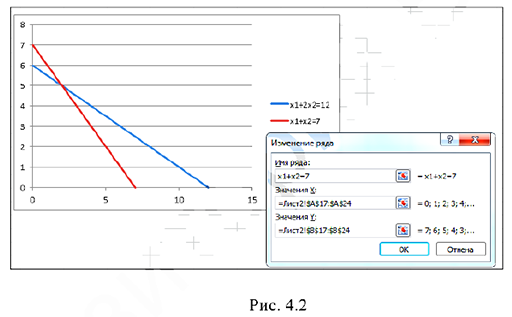
4) Повторить предыдущий пункт для остальных уравнений, входящих в область допустимых решений, а также для градиента и линии уровня.

5) Итоги решения задачи приведены на рисунке 4.3.

Область допустимых решений представляет собой многоугольник с вершинами в точках: (0;0), (0;6), (2;5), (4;3), (5;0).

При перемещении линии уровня в направлении вектора 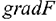получаем оптимальное решение в точке с координатами (2;5), причём

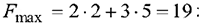
Для получения максимальной прибыли равной 19 д. е. предприятие должно выпускать 2 ед. продукции 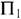и 5 ед. продукции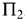

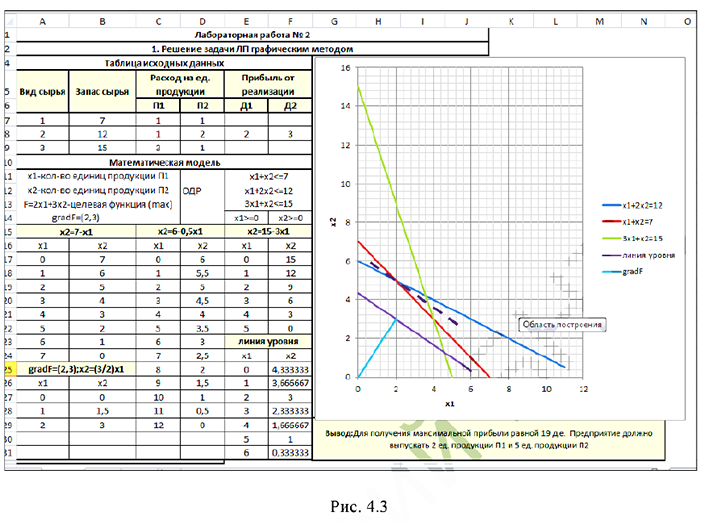
Решение в Microsoft Excel симплекс-методом

Подготовим начальную симплекс таблицу по образцу:

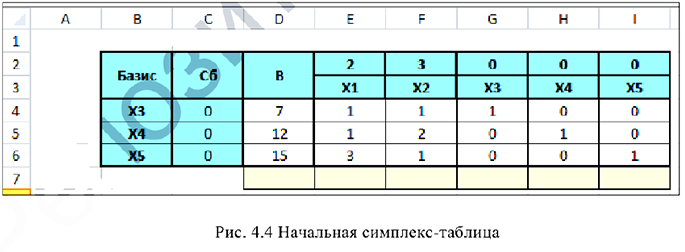
В столбце 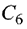этой таблицы записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.

В столбце В записывают положительные компоненты начального опорного плана, в нём же в результате вычислений получают положительные компоненты оптимального плана.

Первые три строки начальной симплекс-таблицы определяются исходными данными задачи, а показатели четвёртой строки — вычисляют. В этой строке в столбце В записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце 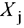— значение

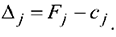
Значение 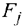находится как скалярное произведение вектора

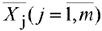
на вектор

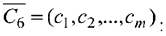
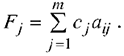
Значение 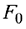равно скалярному произведению вектора 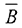на вектор 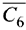Вычислим его и запишем результат в ячейку 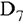. Для вычисления скалярного произведения двух векторов используется функция СУММПРОИЗВ (массив1, [массив2], [массивЗ],…) (рис. 4.5).

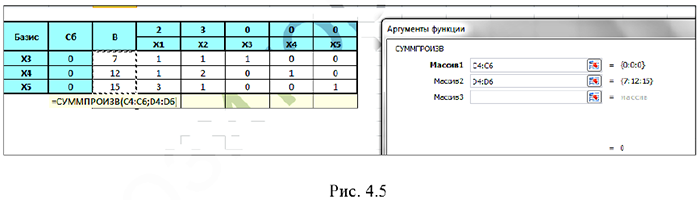
Для вычисления оценок 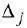используется формула

Выделим ячейку Е7 и введём формулу:

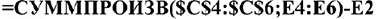
Аналогично вычислим значения других оценок.

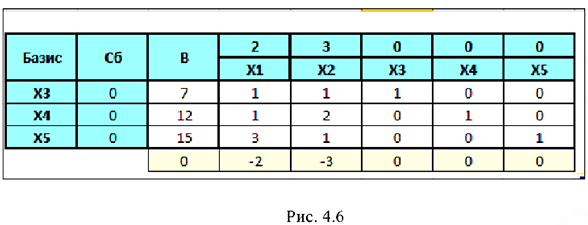
Далее исходный план нужно проверить на оптимальность. Для этого просматриваем элементы последней строки таблицы. В результате может иметь место один из следующих трёх случаев:

1) 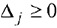— исходный план является оптимальным;

2) 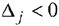для некоторого 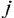и все соответствующие этому индексу величины 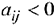— целевая функция не ограничена сверху на множестве планов;

3) 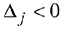для некоторых индексов 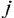и для каждого такого 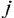по крайней мере одно из чисел 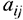является положительным — можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится.

Определим разрешающий столбец — столбец с наибольшей по модулю отрицательной оценкой и найдем отношение элементов столбца В к положительным элементам выбранного столбца для определения разрешающей строки. Для этого выделим ячейку К4 и введём формулу:

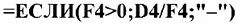
Скопируем формулу на диапазон К4:К6.

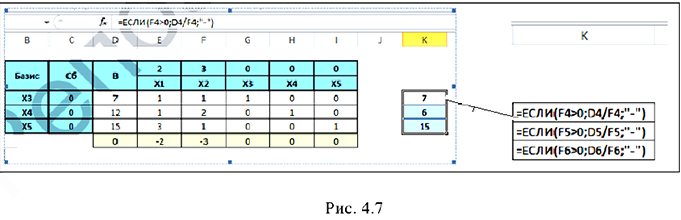
Таким образом, разрешающий столбец — столбец 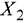и разрешающая строка — .

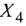Создадим вторую симплекс-таблицу (скопируем предыдущую и удалим все ненужное). Произведём замену в базисе вектора 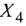(разрешающий столбец) на вектор 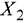(разрешающая строка).

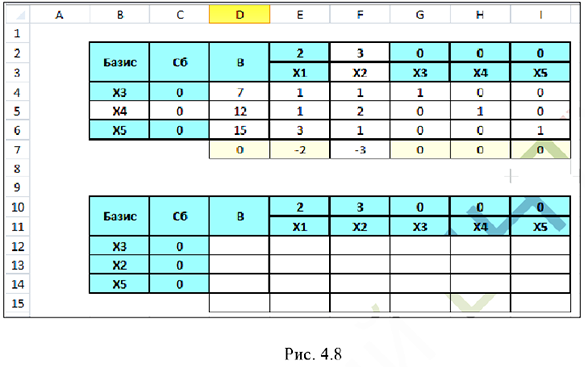
Выделим диапазон D 12:115 и сменим формат числовых данных на дробный.

Вычислим новые элементы разрешающей строки: разделим элементы разрешающей строки на разрешающий элемент. В ячейку D13 введём формулу

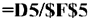
Скопируйте формулу на диапазон Е13: 113:

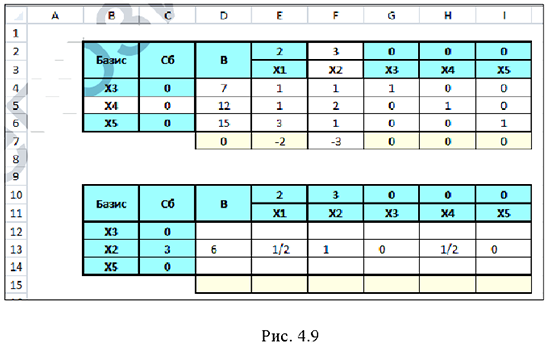
В ячейку D12 введём формулу:

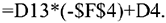
Скопируем формулу на диапазон Е12:I12. В ячейку D14 введём формулу:

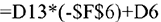
и скопируем формулу на диапазон Е15:115. В ячейку D15 введём формулу:

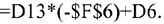
Скопируем формулу на диапазон Е15:I15. Получим:

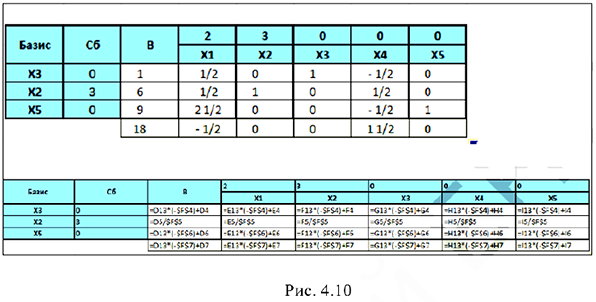
Так как строка оценок содержит отрицательное число, и соответствующий столбец содержит положительные числа, то план можно улучшить. Выбираем разрешающую строку и разрешающий столбец:

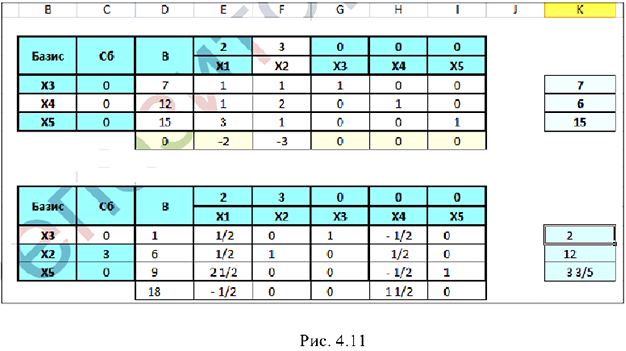
Строим новую симплекс-таблицу и заменяем вектор 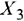(разрешающая строка) на вектор 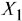(разрешающий столбец). Заполняем таблицу аналогично предыдущей итерации:

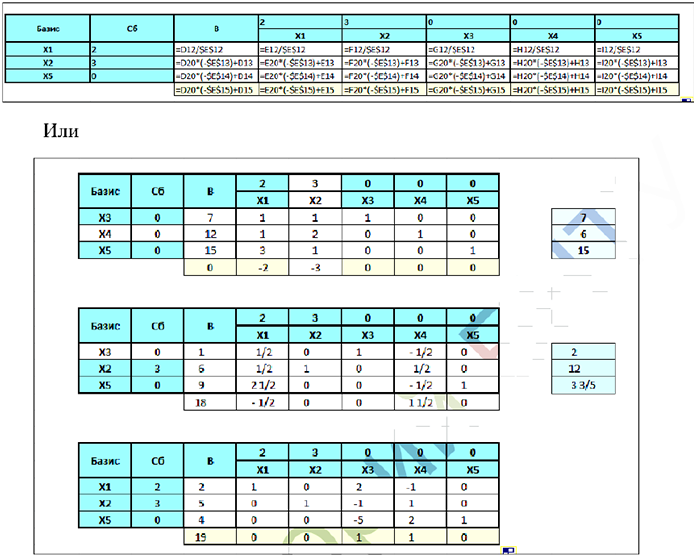
Так как строка оценок не содержит отрицательных значений, то полученный план оптимален и имеет вид:

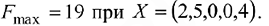
Исключая из решения балансовые неизвестные, получим ответ:

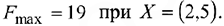
Возможно эта страница вам будет полезна:

Решение задач по линейному программированию

Решение в Microsoft Excel с помощью встроенной функции Поиск решения

В табличном процессоре Microsoft Excel существует встроенная функция Поиск решения, с помощью которой можно решить задачу линейного программирования. Если данный модуль установлен, его можно запустить, выбрав вкладку Данные /Поиск решения. На экране появится диалоговое окно Поиск решения (рис. 4.12).

Если такого пункта во вкладке Данные не оказалось, следует загрузить соответствующую программу-надстройку. Для этого нужно выбрать вкладку Файл-Параметры-Надстройки—Перейти и в диалоговом окне Надстройки установить флажок в строке Поиск решения.

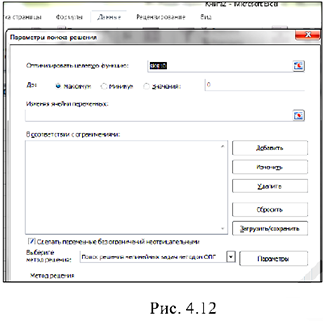
Разберем решение ЗЛП с помощью функции Поиск решения на примере нашей задачи.

• Создадим таблицу для ввода исходных данных: переменных, целевой функции,ограничений.
• Введем начальные нулевые значения для 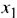и .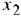
• Зададим целевую функцию в ячейке D6 и ограничения в ячейках F4, F5 и F6 (рис. 4.13).

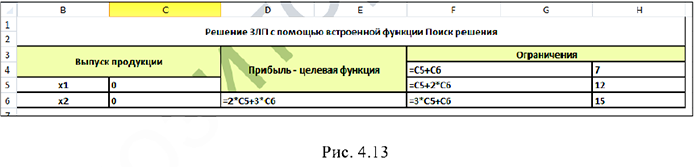
• Выберем команду Данные/Поиск решения, в открывшемся окне Поиск решения установим целевую ячейку D6, зададим условие отыскания максимального значения (рис. 4.14).
• В поле Изменяя ячейки установим ссылку на ячейки С5 и С6, которые будут изменены (молено ввести адреса или имена ячеек с клавиатуры или указать диапазон ячеек на рабочем листе с помощью мыши).
• Определим ограничения, для этого щелчком по кнопке Добавить откроем диалоговое окно Добавление ограничения. Введем ограничения для ячеек F4, F5, F6. Ограничения можно задать как для изменяемых ячеек, так и для целевой ячейки, а также для других ячеек, прямо или косвенно присутствующих в модели (рис. 4.14)

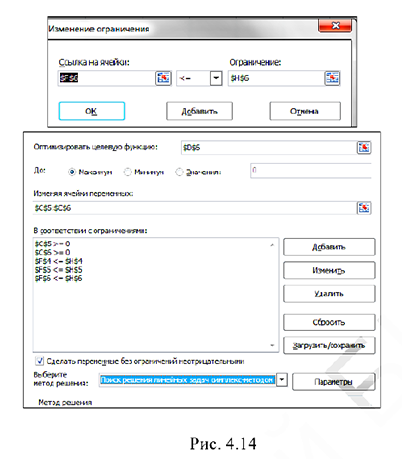
• После того как все параметры и ограничения заданы, запускаем поиск решения, щелкнув на кнопке Найти решение. Когда поиск будет закончен, в таблицу будут внесены новые значения и на экране появится диалоговое окно Результаты поиска решения, сообщающие о завершении операции (рис. 4.15).

Решение найдено. Все ограничения и условия оптимальности выполнены. Сохраним найденное решение. В этом случае таблица будет обновлена. В случае необходимости всегда можно будет восстановить исходные данные с помощью отчета. Для выбора типа отчета достаточно выделить название нужного отчета в списке Тин отчета (или несколько названий, удерживая нажатой клавишу Ctrl). Они будут вставлены на отдельных листах в рабочую книгу перед листом с исходными данными.

Предлагаемые отчеты содержат следующую информацию:

• •отчет Результаты содержит сведения о начальных и текущих значениях целевой ячейки и изменяемых ячеек, а также о соответствии значений заданным ограничениям;
• • отчет Устойчивость отражает найденный результат, а также нижние и верхние предельные значения для изменяемых ячеек;
• •отчет Пределы показывает зависимость решений от изменения формулы или ограничений.

Если планируется использовать созданную модель в дальнейшем, найденное решение можно сохранить как сценарий. Для этого в диалоговом окне Результаты поиска решения необходимо щелкнуть на кнопке Сохранить сценарий.

Возможно эта страница вам будет полезна:

Методы решения задач линейного программирования

Двойственные задачи линейного программирования

Каждой задаче линейного программирования можно поставить в соответствие другую задачу тоже линейного программирования, которая получается из исходной задачи путем определенных преобразований и называется двойственной по отношению к данной исходной задаче.

Т.е. ЗЛП на максимум можно поставить в соответствие ЗЛП на минимум. Эти задачи называются симметричными или взаимно-двойственными.

Рассмотрим понятие двойственных задач на примере следующей задачи.

Задача №5.1.

Предприятие, специализирующееся на производстве трикотажного полотна двух видов, использует для своего производства четыре вида сырья (шерстяную, хлопковую, вискозную, и акриловую нити), запасы которого на планируемый период составляют соответственно 80, 80, 260 и 410 бобин. В приведенной ниже таблице даны технологические коэффициенты, т.е. расход каждого вида сырья на производство одного метра каждого вида трикотажа.

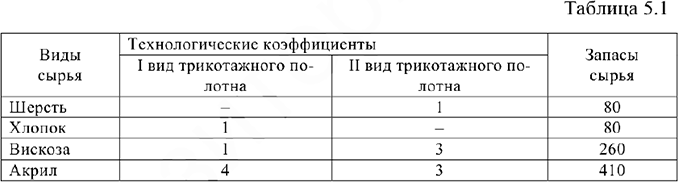
Прибыль от реализации 1 м трикотажного полотна первого вида составляет 2 д. е., а трикотажного полотна второго вида 3 д. е. Необходимо определить оптимальный план выпуска трикотажного полотна первого и второго вида, чтобы обеспечить максимальную прибыль от их реализации.

Экономико-математическая модель задачи: найти максимум целевой функции (функции прибыли):

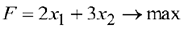
при выполнении системы ограничений:

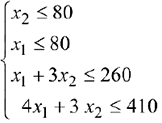
Предположим, что некоторая организация решила закупить ресурсы предприятия и необходимо установить оптимальные цены на эти ресурсы .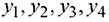

Очевидно, что покупающая организация заинтересована в том, чтобы затраты на все ресурсы (целевая функция 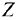) в количествах 80, 80, 260 и 410 д. е. по ценам 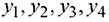были минимальны, т.е.

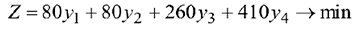
С другой стороны, предприятие, продающее ресурсы, заинтересовано в том. чтобы полученная выручка была не менее той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию.

На изготовление 1 м трикотажного полотна I вида расходуется 0 д. е. первого ресурса (шерсти), 1 д. е. второго ресурса (хлопка), 1 д. е. третьего ресурса (вискозы) и 4 д. е. четвертого ресурса (акрила). Поэтому для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении 1 м трикотажного полотна I вида по ценам 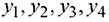, должны быть не менее цены 1 м трикотажного полотна 1 вида (2 д. е.), т.е.

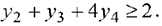
Аналогично составим ограничение в виде неравенства по второму виду продукции (трикотажному полотну II вида):

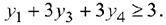
Таким образом, получили двойственную задачу относительно исходной (таблица 5.2).

При этом цены ресурсов 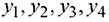являются условными, в отличие от «внешних цен» на продукцию, известных, как правило, до начала производства.

Цены ресурсов 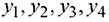так же называются «внутренними» (или оценками ресурсов), т.к. они задаются не извне, а определяются непосредственно в результате решения задачи.

Исходную задачу можно рассматривать как двойственную по отношению к своей двойственной задаче, т.е. обе задачи являются взаимно двойственными.

Взаимно двойственные задачи обладают следующими свойствами:

1. В одной задаче определяется максимум целевой функции, в другой — минимум.
2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой.
3. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида 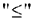, а в задаче минимизации — все неравенства вида.
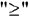4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных имеются в обеих задачах.

Алгоритм составления двойственной задачи

1. Привести все неравенства системы ограничений исходной задачи к одному виду: если в исходной задаче ищут максимум целевой функции, то все неравенства системы ограничений привести к виду 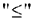, а если минимум — к виду 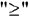. Для этого неравенства, в которых данное требование не выполняется, умножить на (-1).
2. Составить расширенную матрицу системы ограничений исходной задачи — матрицу 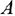, в которую включить строку коэффициентов при переменных в целевой функции.
3. Найти матрицу 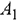, транспонированную к матрице .
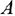4. Сформулировать двойственную задачу на основании полученной матрицы 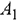, и условия неотрицательности переменных.

Двойственная задача может быть решена симплекс-методом, а так же с помощью функции Поиск решения в табличном редакторе Microsoft Excel.

Если же исходная задача уже решена симплекс-методом, то решение двойственной задачи может быть найдено по формуле:

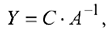
где 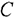— матрица-строка коэффициентов при базисных переменных целевой функции входящих в оптимальный базис исходной задачи (в первоначальном виде); 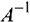— обратная матрица для матрицы 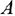, являющейся матрицей коэффициентов при переменных, входящих в оптимальный базис (взятых из первоначальной системы ограничений исходной задачи).

Вернёмся к задаче 5.1. Решим прямую задачу симплекс-методом.

Приведем ЗЛП к каноническому виду.

Для этого приведем систему неравенств к системе уравнений путем введения дополнительных переменных .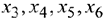

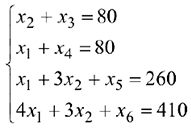
Определение первоначального допустимого базисного решения.

Т.к. каждая дополнительная переменная входит в уравнение с тем же знаком, что и свободный член, стоящий в правой части уравнения, то в качестве базисных переменных можно взять дополнительные 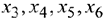и при этом получим допустимое базисное решение.

Замечание: Базисные переменные — это переменные, которые входят только в одно уравнение системы ограничений и при этом имеют коэффициент, равный единице.

Полагая, что свободные переменные 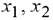равны 0, получим первое базисное решение:

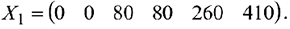
Данное базисное решение является допустимым, т.к. оно неотрицательно.

Составление симплекс-таблицы.

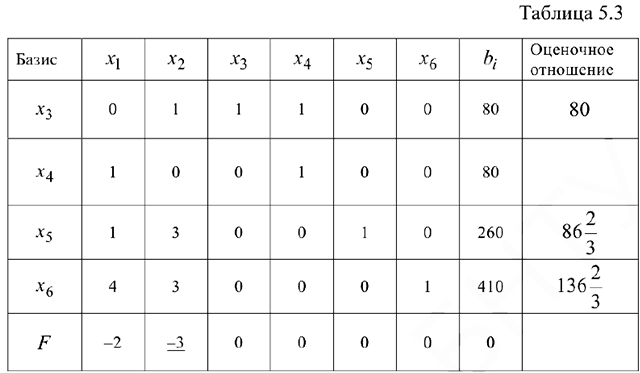
Получено первоначальное допустимое базисное решение, целевая функция содержит только свободные переменные, переходим к составлению первой симплекс-таблицы (таблица 5.3):

Переход к основному алгоритму симплекс-метода.

I шаг.

• Проверка критерия оптимальности.

Полученное на I шаге базисное решение (опорный план) не является оптимальным, т.к. в индексной строке есть отрицательные коэффициенты.

• Определение новой базисной переменной.

В качестве разрешающего выберем столбец, соответствующий переменной 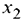, т.к. ей соответствует наибольший по модулю отрицательный коэффициент (-3).

• Определение новой свободной переменной.

Вычислим оценочные отношения для строк соответствующих базисным переменным 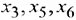как частное от деления 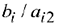(т.к. эти строки содержат положительные коэффициенты в разрешающем столбце). Выберем из полученных значений наименьшее:

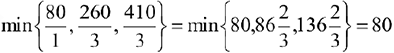
Следовательно, первая строка (соответствующая базисной переменной 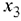) является разрешающей. Разрешающий элемент — 1, который находится на пересечении разрешающего столбца и разрешающей строки.

• Пересчет симплекс-таблицы.

В столбце базисных переменных записываем новый базис: вместо базисной переменной 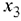— переменную .

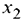В столбцах, соответствующих базисным переменным проставляем нули и единицы: 1 — против «своей» базисной переменной; 0 — против «чужой» базисной переменной; 0-в последней индексной строке для всех базисных переменных.

Все остальные элементы новой симплекс-таблицы (включая элементы индексной строки) находим по правилу «прямоугольника».

После преобразований получаем новую таблицу (таблица 5.4).

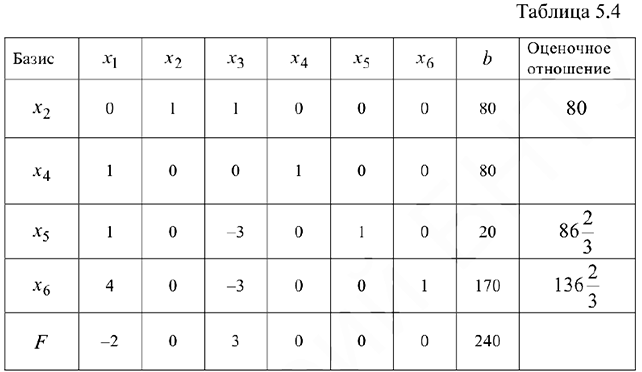
Базисное решение:

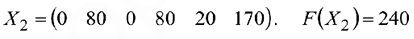
II шаг.

• Проверка критерия оптимальности.

Полученное на II шаге базисное решение (опорный план) не является оптимальным, т.к. в индексной строке есть отрицательный коэффициент (-2).

• Определение новой базисной переменной.

В качестве разрешающего выберем столбец, соответствующий переменной 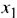, т.к. ей соответствует отрицательный коэффициент (-2).

• Определение новой свободной переменной.

Вычислим оценочные отношения для строк соответствующих базисным переменным 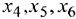как частное от деления 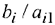(т.к. эти строки содержат положительные коэффициенты в разрешающем столбце). Выберем из полученных значений наименьшее:

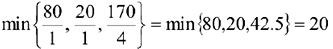
Следовательно, третья строка (соответствующая базисной переменной 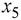) является разрешающей. Разрешающий элемент 1, который находится на пересечении разрешающего столбца и разрешающей строки.

• Пересчет симплекс-таблицы.

В столбце базисных переменных записываем новый базис.

Разрешающий элемент — 1. В столбцах, соответствующих базисным переменным проставляем нули и единицы: 1 — против «своей» базисной переменной; 0 — против «чужой» базисной переменной; О-в последней индексной строке для всех базисных переменных. Все остальные элементы новой симплекс-таблицы (включая элементы индексной строки) находим по правилу «прямоугольника».

После преобразований получаем новую таблицу (таблица 5.5).

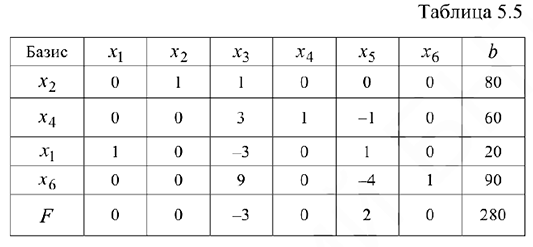
Базисное решение

III шаг.

• Проверка критерия оптимальности.

Полученное на 11 шаге базисное решение (опорный план) не является оптимальным, т.к. в индексной строке есть отрицательный коэффициент (-3).

• Определение новой базисной переменной.

В качестве разрешающего выберем столбец, соответствующий переменной 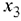, т.к. ей соответствует отрицательный коэффициент (-3).

• Определение новой свободной переменной.

Вычислим оценочные отношения для строк соответствующих базисным переменным 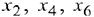как частное от деления: 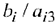(т.к. эти строки содержат положительные коэффициенты в разрешающем столбце). Выберем из полученных значений наименьшее:

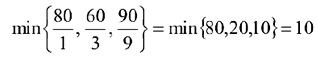
Следовательно, четвертая строка (соответствующая базисной переменной 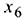) является разрешающей. Разрешающий элемент 9, который находится на пересечении разрешающего столбца и разрешающей строки.

• Пересчет симплекс-таблицы.

В столбце базисных переменных записываем новый базис. Каждый элемент разрешающей строки (которая в новой симплекс таблице будет уже соответствовать переменной 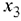) делим на разрешающий элемент (РЭ=9).

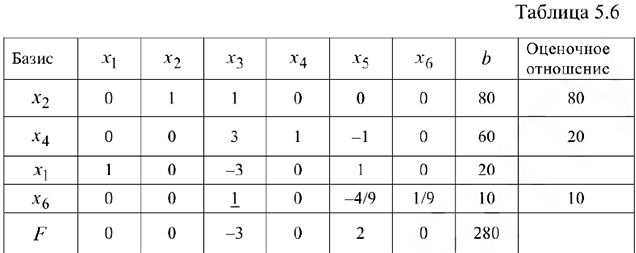
На месте разрешающего элемента получаем 1. В столбцах, соответствующих базисным переменным проставляем нули и единицы: 1 — против «своей» базисной переменной; 0 — против «чужой» базисной переменной; О-в последней индексной строке для всех базисных переменных.

Все остальные элементы новой симплекс-таблицы (включая элементы индексной строки) находим по правилу «прямоугольника» После преобразований получаем новую таблицу.

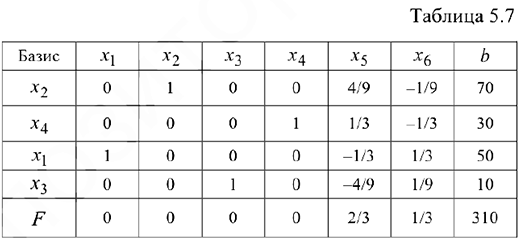
Базисное решение

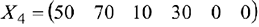
Полученное базисное решение (опорный план) является оптимальным, т.к. в индексной строке нет отрицательных коэффициентов. Таким образом, оптимальным будет решение:

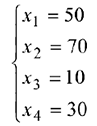
при котором

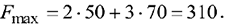
Т.е. для получения максимальной прибыли от реализации трикотажного полотна в размере 310 д. е. предприятие должно выпустить за планируемый период соответственно 50 и 70 метров трикотажного полотна первого и второго вида.

Рассмотрим последний шаг решения прямой задачи. Составим матрицу 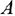из коэффициентов при переменных, входящих в оптимальный базис (взятых из первоначальной системы ограничений исходной задачи)

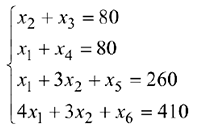
Матрица коэффициентов

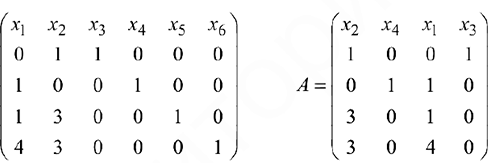
Найдем обратную матрицу 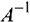в табличном редакторе Microsoft Excel с помощью встроенной функции МОБР().

Для этого необходимо:

1) Выделить область для вывода обратной матрицы;

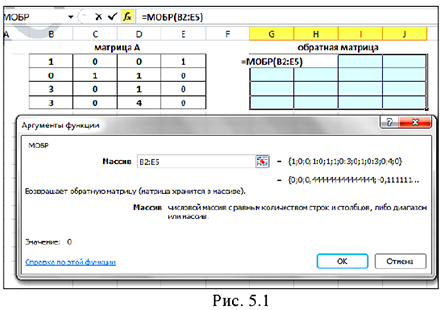
2) Вызвать функцию =МОБР() (рис. 5.1);

3) После выделения диапазона исходных данных одновременно нажать комбинацию клавиш CTRL-SHIFT-ENTER.

В результате получим (рис. 5.2):

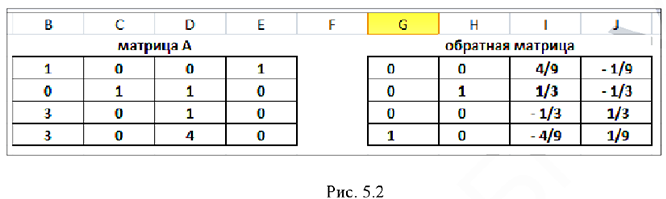
То есть:

Тогда:

Или, применяя встроенную функцию МУМНОЖ (рис. 5.3):

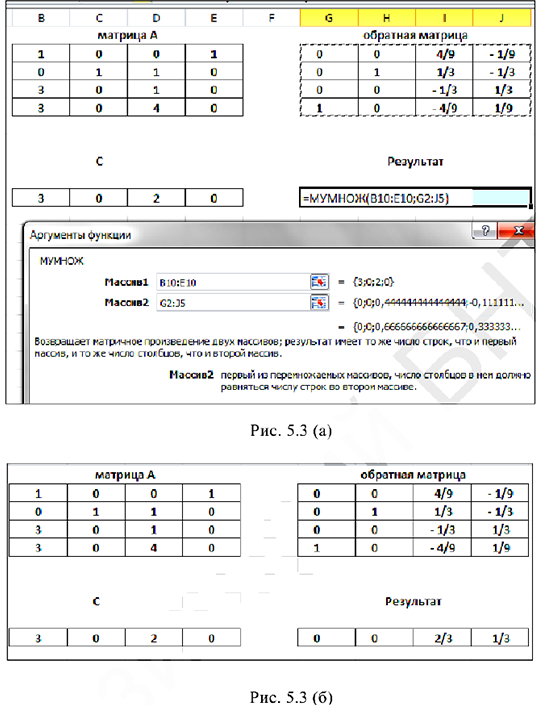
Т.е. оптимальный план двойственной задачи равен:

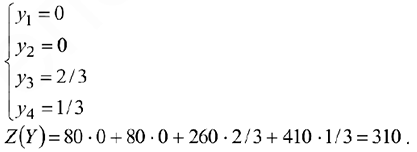
Возможно эта страница вам будет полезна:

Графическое решение задач линейного программирования

Двойственный симплекс-метод. Анализ экономико-математической модели двойственной задачи

Рассмотрим симплексный алгоритм, который основан на соотношениях между прямой и двойственной задачами. Этот алгоритм эффективно решает определенный класс задач линейного программирования.

В двойственном симплекс-методе решение задачи линейного программирования начинается с недопустимого, но лучшего, чем оптимальное решения. Последовательные итерации этого метода приближают решение к области допустимости без нарушения оптимальности промежуточных решений. Когда будет достигнута область допустимых решений, процесс вычислений заканчивается, так как последнее решение будет оптимальным.

В двойственном симплекс-методе начальная симплекс-таблица обязательно должна иметь в базисном решении недопустимую (т.е. отрицательную) переменную. Для реализации двойственного симплекс-метода разработаны следующие два условия, выполнение которых гарантирует оптимальность последовательных промежуточных решений и приближение их к области допустимых решений.

Двойственное условие допустимости. В качестве исключаемой переменной 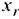выбирается базисная переменная, имеющая наибольшее по абсолютной величине отрицательное значение. Если таких переменных несколько, то выбор произволен. Если все базисные переменные неотрицательные, процесс вычислений заканчивается.

Двойственное условие оптимальности. Вводимая в базис переменная определяется как переменная, на которой достигается следующий минимум:

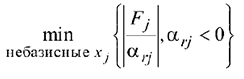
где 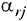— коэффициент из симплекс-таблицы, расположенный на пересечении ведущей строки (соответствующей исключаемой переменной 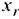) и столбца, соответствующего переменной 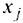. При наличии нескольких альтернативных переменных, выбор делается произвольно.

Задача №6.1.

Дана задача линейного программирования:

Минимизировать

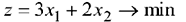
При ограничениях

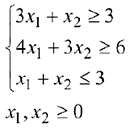
Начальная симплекс-таблица имеет вид:

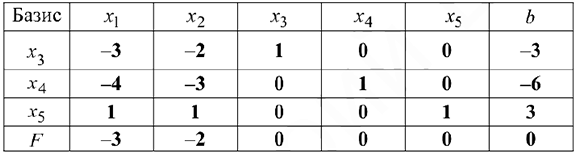
Среди дополнительных переменных этой задач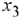и и 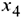являются избыточными, а 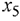— остаточной. Умножим каждое равенство, соответствующее избыточным дополнительным переменным, на -1; в результате правые части этих равенств непосредственно указывают на базисные переменные, которые являются недопустимыми 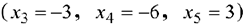. Этот подход всегда используется при реализации двойственного симплекс-метода.

Поскольку элементы в индексной строке отрицательны для всех 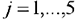начальное базисное решение является оптимальным (но не допустимым). Таким образом, приведенная таблица удовлетворяет требованиям начальной таблицы двойственного симплекс-метода, а именно оптимальности и недопустимости.

Двойственное условие допустимости указывает на переменную 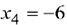как на исключаемую из базиса. Теперь применим двойственное условие оптимальности для определения переменной, вводимой в базис. Для этого используем следующую таблицу.

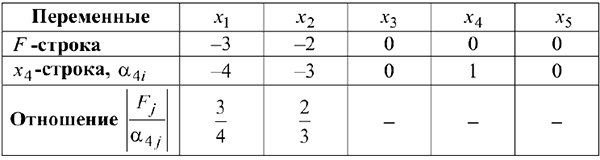
Приведенные отношения показывают, что вводимой в базис переменной будет .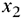

Следующая таблица получена с помощью известных операций над строками, применяемых в прямом симплекс-методе.

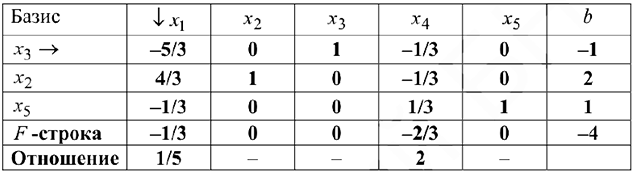
Последняя таблица показывает, что из базиса исключается переменная 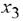и вводится 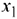. В результате получаем следующую симплекс-таблицу.

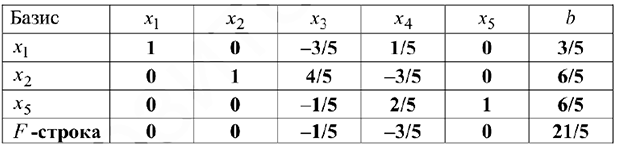
Решение, представленное в последней таблице, допустимо (и оптимально), поэтому вычисления заканчиваются. Это решение имеет вид

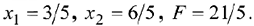
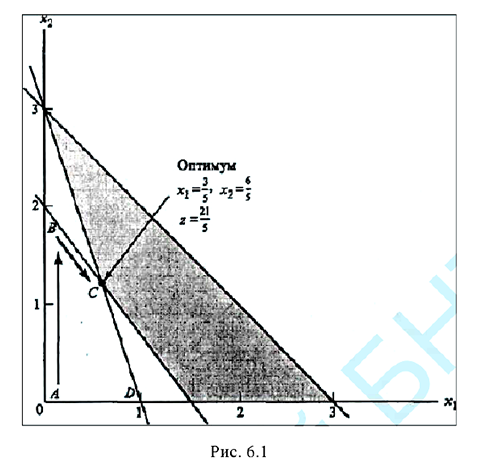
На рис. 6.1 показана последовательность шагов двойственного сим-плекс-метода при решении этой задачи.

Алгоритм начинается в крайней точке А (которой соответствует недопустимое, но «лучше, чем оптимальное» решение), затем он переходит к точке В (которой также соответствует недопустимое, но «лучше, чем оптимальное» решение) и заканчивается в точке С, уже принадлежащей области допустимых решений.

Возможно эта страница вам будет полезна:

Графический метод решения задач линейного программирования

Задача №6.2.

На предприятии имеется возможность выпуска трех видов продукции 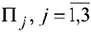. При её изготовлении используются ресурсы 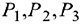. Размеры допустимых затрат ресурсов ограничены соответственно величинами 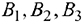. Расход ресурса 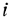-го вида на единицу продукции 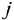-го вида составляет 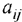единиц. Цена единицы продукции 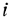-го вида равна .

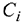Требуется:

• Найти план продукции, обеспечивающий предприятию максимальный доход.
• Сформулировать в экономических терминах двойственную задачу, составить математическую модель двойственной задачи и решить её.
• Используя решение исходной и двойственных задач, а также соответствие между двойственными переменными, провести анализ плана, указать наиболее дефицитный и избыточный ресурс, если он имеется.

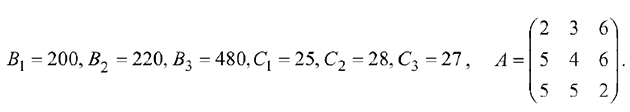
Решение:

Пусть 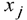— это количество единиц продукции соответственно 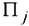, планируемой к выпуску, a 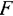— величина прибыли от реализации этой продукции.

Составим экономико-математическую модель задачи. Учитывая значение прибыли от единицы продукции, запишем суммарную величину прибыли целевую функцию — в следующем виде.

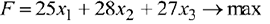
Переменные 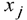должны удовлетворять ограничениям, накладываемым на расход ресурсов, имеющихся в распоряжении предприятия:

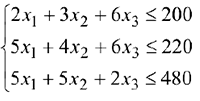
По смыслу задачи переменные должны быть неотрицательными:

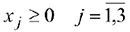
Решаем задачу в MS Excel. Составим следующую таблицу:

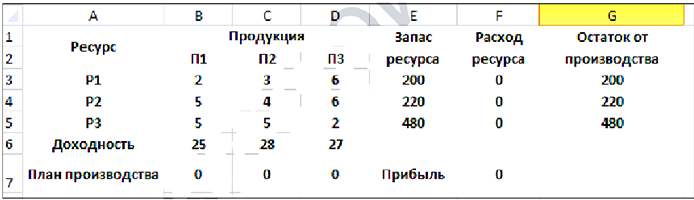
Формулы использовали следующие:

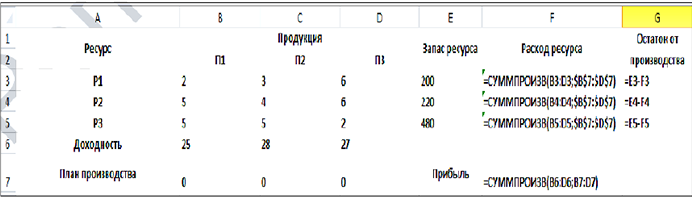
Выполняем последовательность команд: Данные — Поиск решения. Поля в появившемся окне заполняем следующим образом:

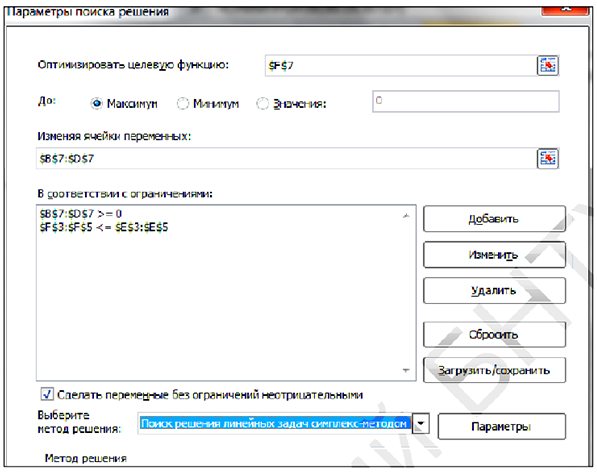
Нажимаем кнопку «Найти решение», получаем результат:

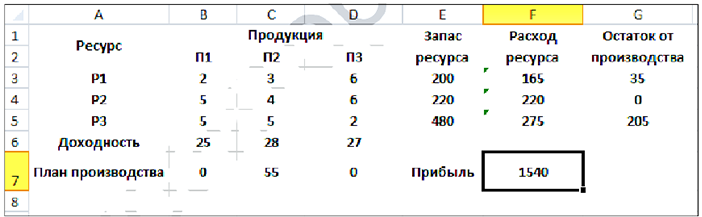
Т.о., по оптимальному плану следует изготовить 55 ед. продукции второго вида, продукцию первого и третьего вида — не выпускать. Останутся неиспользованными 35 ед. первого ресурса и 205 ед. третьего ресурса. Прибыль при этом будет максимальна и составит 1540 ден. ед.

Составим экономико-математическую модель двойственной задачи.

Пусть 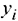— цена единицы ресурса 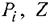— суммарная стоимость ресурсов. Требуется минимизировать затраты покупающего ресурсы предприятия, при этом нашему предприятию продажа должна быть менее выгодна, чем производство продукции.

Двойственная задача:

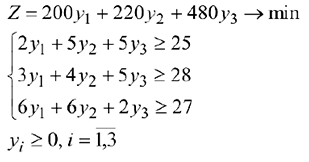
Решаем задачу в MS Excel. Первоначальная таблица:

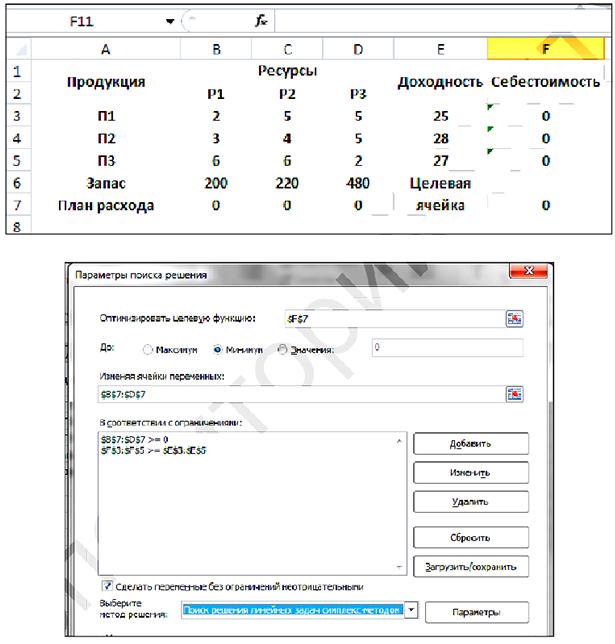
Результаты:

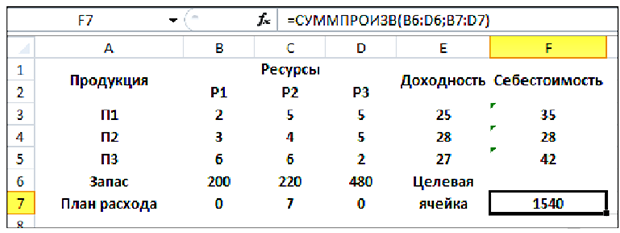
Соответствие между переменными:

Запишем оптимальный план двойственной задачи:

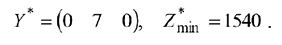
Так как 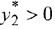, то второй ресурс дефицитен, первый и третий ресурсы являются избыточными для них .

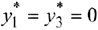При увеличении использования второго ресурса на единицу прибыль увеличиться па 7 денежных ед., первого и третьего — прибыль не изменится.

Возможно эта страница вам будет полезна:

Заказать работу по линейному программированию

Транспортная задача (тз)

Одним из частных случаев задач линейного программирования является транспортная задача. Цель данной задачи состоит в определении оптимального плана перевозок, при котором минимальной была либо стоимость перевозок, либо минимальным было время доставки груза.

В общем виде транспортную задачу можно представить следующим образом: в 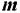пунктах производства 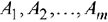имеется однородный груз в количествах, соответственно, 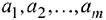. Этот груз необходимо доставить в 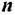пунктов назначения 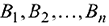в количествах, соответственно 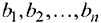. Стоимость перевозки 1 ед. груза (тариф) из пункта 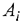в пункт 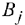равна .

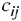Требуется составить план перевозок так, чтобы:

1. мощности (запасы) всех поставщиков были реализованы;
2. заказы всех потребителей были удовлетворены;
3. суммарные затраты на перевозку были бы минимальны.

Исходные данные транспортной задачи записываются в виде таблицы 8.1

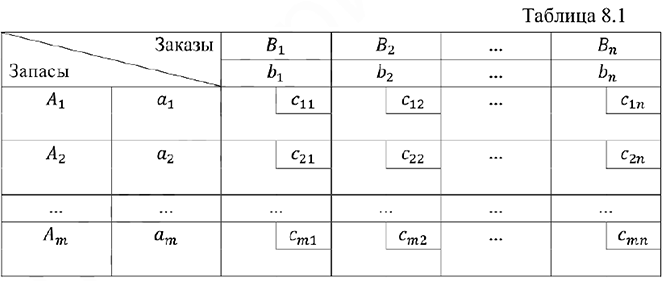
Виды транспортных задач

В зависимости от соотношения между суммарными запасами груза у поставщиков и суммарными потребностями в нем потребителей транспортные задачи делятся на два вида: закрытые и открытые.

Определение 8.1. Если сумма запасов груза у поставщиков равна суммарной потребности в нем потребителей, т.е.

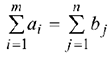
то транспортная задача называется закрытой. Определение 2. Если условие (8.1) не выполняется, т.е.

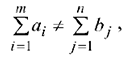
то транспортная задача называется открытой.

Теорема 8.1 (необходимое и достаточное условие разрешимости ТЗ). Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т.е. чтобы выполнялось равенство (8.1).

Возможно эта страница вам будет полезна:

Помощь по линейному программированию

Математическая модель закрытой транспортной задачи

Рассмотрим закрытую транспортную задачу.

• Неизвестными транспортной задачи являются 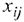— объёмы перевозок or каждого 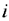— го поставщика каждому 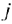-му потребителю. Эти переменные так же можно записать в виде матрицы перевозок:

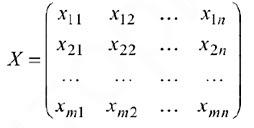
• Так как произведение 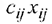определяет затраты на перевозку груза от 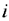-го поставщика 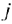-му потребителю, то суммарные затраты на перевозку всех грузов равны 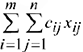. Т.е. целевая функция будет иметь вид:

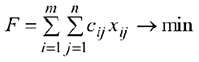
• Система ограничений транспортной задачи состоит из двух групп уравнений.

Первая группа состоит из 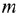уравнений и описывает тот факт, что запасы всех поставщиков 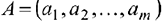вывозятся полностью, т.е.:

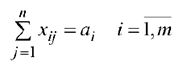
Вторая группа состоит из 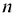уравнений и выражает требование полностью удовлетворить запросы всех 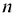потребителей:

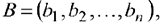
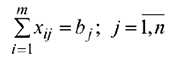
Кроме того, переменные 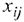должны быть неотрицательны:

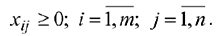
• Оптимальным решением транспортной задачи является матрица размерности 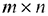, удовлетворяющая системе ограничений и обеспечивающая минимум целевой функции.

Особенности экономико-математической модели ТЗ

1. Система ограничений представляет собой систему уравнений (т.е. ТЗ задана в канонической форме);
2. Коэффициенты при переменных системы ограничений равны единице или нулю;
3. Каждая переменная входит только в два уравнения системы ограничений.

Число переменных 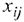в ТЗ с 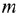пунктами отправления и 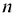пунктами назначения равно 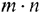, а число уравнений в системах (8.2) и (8.3) равно 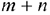. Так как мы предполагаем, что выполняется условие (8.1), то число линейно независимых уравнений равно 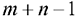. Следовательно, опорный план транспортной задачи, может иметь не более 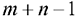отличных от нуля неизвестных.

Если в опорном плане число отличных от нуля неизвестных равно 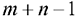, то план является невырожденным, а если меньше — то вырожденным.

Возможно эта страница вам будет полезна:

Контрольная работа по линейному программированию

Открытая транспортная задача (транспортная задача с нарушенным балансом)

В открытой ТЗ сумма запасов не совпадает с суммой потребностей, поэтому для решения открытой ТЗ ее сводят к закрытой ТЗ.

• Если 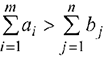, т.е. суммарный запас груза поставщиков больше суммарного спроса потребителей, то в задачу вводится фиктивный 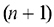-й потребитель с потребностью равной разности объемов запаса и потребления 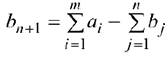и стоимостью перевозок

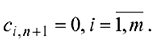
• Если 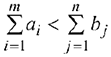т.е. объем потребления превышает объем запасов, то вводится фиктивный 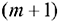-й поставщик с запасом 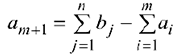и стоимостью перевозок .

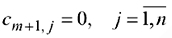После добавления фиктивного потребителя или фиктивного поставщика ТЗ становится закрытой, а, следовательно, и разрешимой.

Транспортная задача как задача линейного программирования может быть решена симплекс-методом, однако наличие большого числа переменных и ограничений делает вычисления громоздкими. Поэтому для решения данного класса задач разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно:

1. Нахождение исходного опорного решения;
2. Проверка полученного решения на оптимальность;
3. Переход от одного опорного решения к другому до достижения оптимального значения (минимума) целевой функции.

При решении ТЗ ее условие и исходное опорное решение записывается в распределительную таблицу. Клетки, в которых записан объем перевозки от 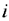-го поставщика к 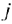-му потребителю называются занятыми, им соответствуют базисные переменные опорного решения. Остальные, незанятые клетки называются пустыми и им соответствуют свободные переменные. В верхнем правом углу каждой клетки записывается тариф перевозки груза от данного 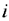-го поставщика к 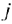-му потребителю.

При распределении грузов может оказаться, что количество занятых клеток меньше, чем 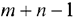(в случае вырожденной транспортной задачи). В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми. Нулевую поставку помещают в свободную клетку с наименьшим тарифом, причем чтобы в каждой строке и столбце было не менее одной занятой клетки.

Для определения исходного опорного плана ТЗ существует несколько методов. Рассмотрим на примере два из них: метод «северо-западного угла» и метод минимального элемента (метод наименьшей стоимости).

Задача №8.1.

На складах 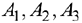имеются запасы продукции в количествах 90, 400, 110 т соответственно. Потребители 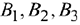должны получить эту продукцию в количествах 140, 300, 160 т соответственно. Построить первоначальный допустимый опорный план закрепления потребителей за поставщиками. Найти оптимальный план закрепления потребителей за поставщиками, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей 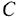в денежных единицах.

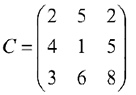
Решение:

Запишем исходные данные задачи в виде таблицы 8.2

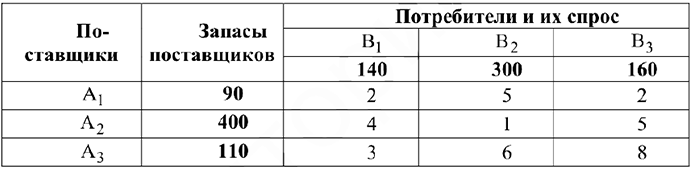
Математическая модель задачи

Матрица перевозок:

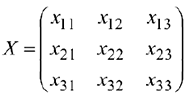
Система ограничений:

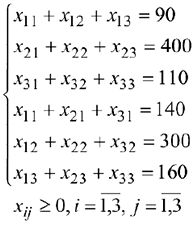
Целевая функция:

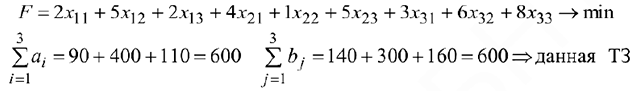
является закрытой, необходимое и достаточное условие разрешимости задачи выполнено.

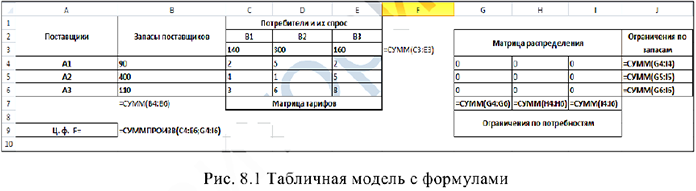
Запись математической модели данной транспортной задачи в табличном редакторе Microsoft Excel имеет вид (рис. 8.1).

• Найдем исходное опорное решение методом «северо-западного угла»:

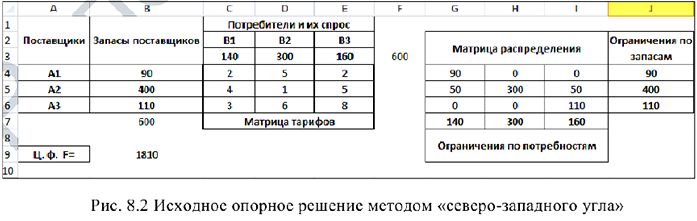
В результате получен исходный опорный план, который является допустимым, так как все грузы (запасы поставщиков) вывезены, спрос потребителей удовлетворен, т.е. план соответствует системе ограничений ТЗ.

Число занятых клеток в таблице равно 5,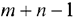 =3 + 3-1 = 5 , т.е. условие невырожденности выполнено. Получим исходное опорное решение:

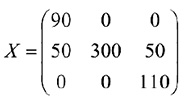
Стоимость перевозки (значение целевой функции) при исходном опорном решении составляет:

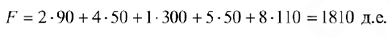
Метод минимального тарифа (элемента) (метод наименьших затрат)

Согласно этому методу, грузы распределяются в первую очередь в те клетки, в которых находится минимальный тариф перевозок 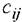. Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс распределения продолжают до тех пор, пока все грузы от поставщиков не будут вывезены, а спрос всех потребителей не будет удовлетворен.

Найдем исходное опорное решение для примера 8.1 методом минимального элемента:

Возможны два варианта

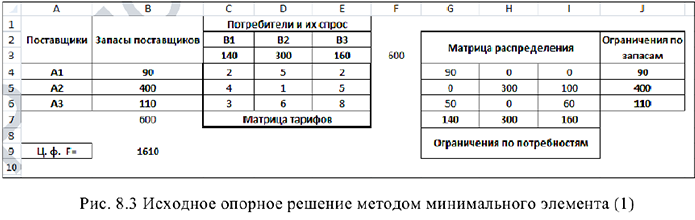
Опорный план:

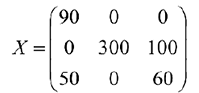
Стоимость перевозки (значение целевой функции):

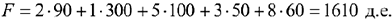
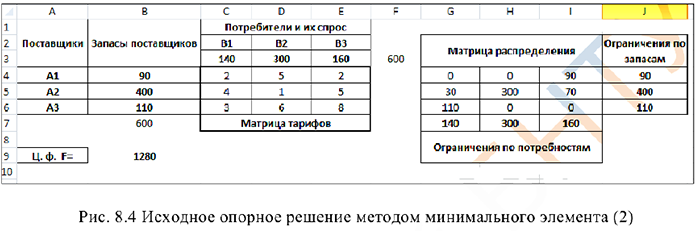
Опорный план:

Стоимость перевозки (значение целевой функции):

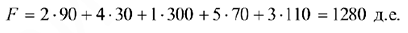
Проверка оптимальности плана и перераспределение поставок с помощью метода потенциалов.

Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.

Покажем, как нужно пользоваться методом потенциалов на примере первоначального плана, полученного выше по методу северозападного угла (рис. 8.2).

Найдем потенциалы по базисным (загруженным) клеткам таблицы с помощью формул

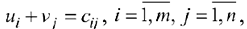
положив и :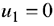

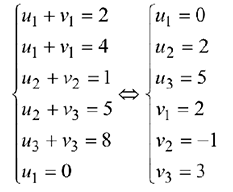
Вычисляем оценки

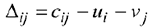
свободных клеток:

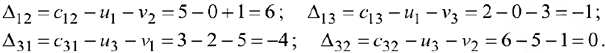
Среди оценок имеются отрицательные, поэтому план не оптимален, его следует преобразовать в новый план. Занесём оценки в таблицу. Получим:

В левых нижних углах соответствующих клеток находятся оценки .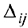

Чтобы улучшить план перевозок, необходимо для свободной клетки распределительной таблицы, имеющей отрицательную оценку, построить цикл пересчёта (цикл), который позволяет перераспределить занятые клетки так, чтобы получить новый план перевозок с меньшими суммарными затратами.

Цикл — совокупность клеток распределительной таблицы, из которых только одна клетка свободная, та, для которой строится цикл. Клетки, составляющие цикл, расположены в углах замкнутой ломаной линии, каждый отрезок которой лежит на одном и том же столбце распределительной таблицы.

Каждой клетке цикла поставим в соответствие знаки «+» и «—», которые при обходе цикла будут чередоваться. При этом свободную клетку (начальную клетку цикла) всегда считаем положительной.

Строим цикл с началом в клетке (3,1) с минимальной оценкой 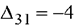, он будет включать в себя клетки (см. таблицу 8.4):

Величина груза, перемещаемая с помощью цикла равна наименьшей из величии, расположенных в отрицательных клетках:

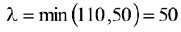
Найденную величину прибавим в положительных клетках цикла и вычтем в отрицательных. Клетка (2,1) станет свободной. Получим новый план перевозок, который занесём в таблицу 8.4:

Опорный план:

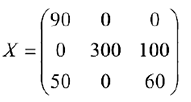
Стоимость перевозки (значение целевой функции):

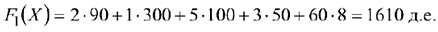
Построена таблица с новым планом, состоящим из старых поставок, не вовлечённых в цикл и новых — в вершинах рассмотренного цикла. Проведём перерасчёт потенциалов 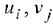и оценок :

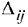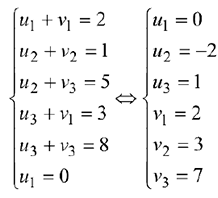
Оценки для незанятых клеток:

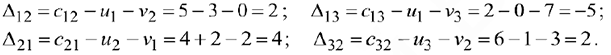
Наличие отрицательной оценки говорит о том, что данный план не является оптимальным.

Внесём данные в таблицу (таблица 8.5):

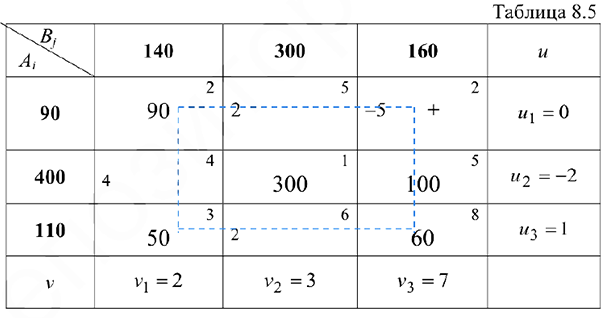
Строим цикл с началом в клетке (1,3) с оценкой 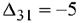включать в себя клетки (см. таблицу 8.5):

Тогда

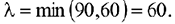
Перераспределим груз по циклу, указанному в таблице 6.5 пунктиром на величину 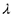. Получим следующую распределительную таблицу:

Опорный план:

Стоимость перевозки (значение целевой функции):

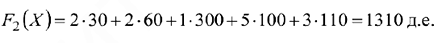
Проверим план на оптимальность. Потенциалы:

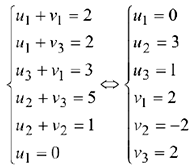
Оценки для незанятых клеток:

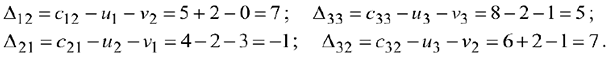
План не является оптимальным, так как 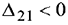. Его нужно преобразовать в новый план, загрузив клетку (2,1). Цикл (см. таблицу 8.7):

По этому контуру находим поставку

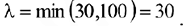
Прибавляем 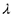к элементам, стоящим у вершин со знаком (+) и вычитаем из элементов, стоящих у вершин со знаком (-). Получаем новое опорное решение (см. таблицу 8.8)

Стоимость перевозки (значение целевой функции):

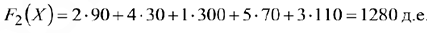
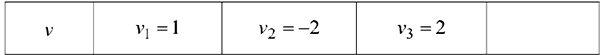
Исследуя этот план аналогично предыдущим, находим потенциалы (они приведены в таблице 8.8), и по ним — оценки свободных клеток:

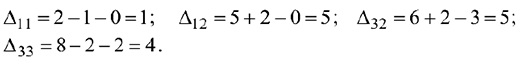
Отрицательных оценок нет, следовательно, в таблице содержится оптимальный план.

Табличная модель.

Вводим данные в таблицу Excel

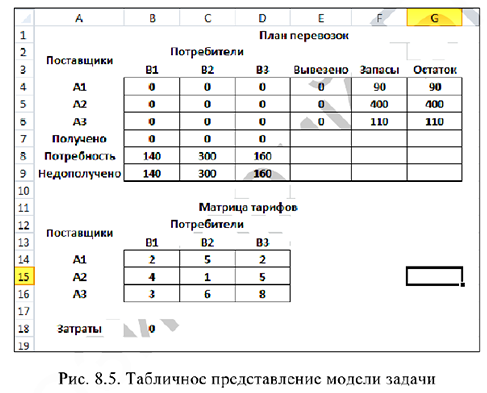
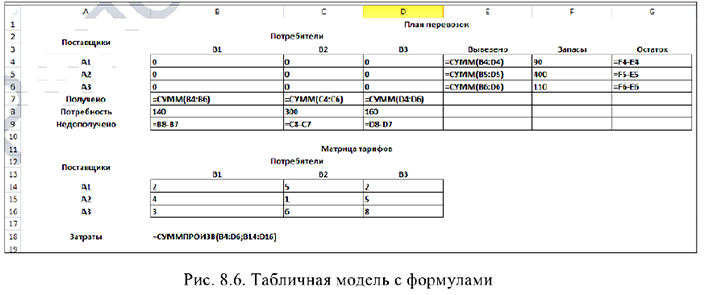
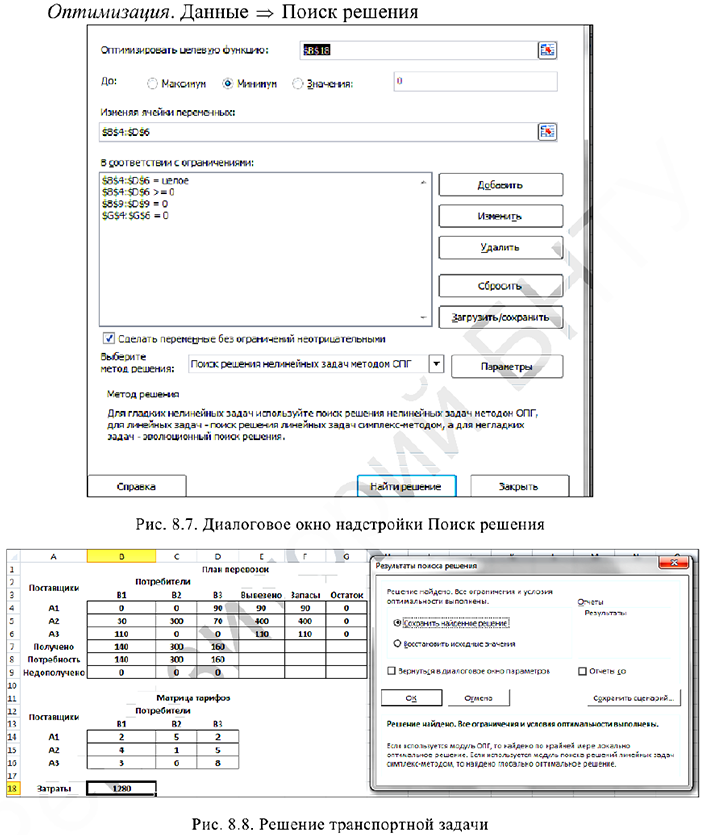
Вывод: Минимальные суммарные затраты на перевозку груза равны 1280 д.е. Они достигаются путем распределения поставок, представленных в ячейках [B4:D6]. Так, например, поставщик А1 должен доставить груз только потребителю ВЗ в количестве 90 единиц. Поставщик А2 должен поставить груз к потребителю В1 в количестве 30 ед., к потребителю В2 300 единиц и к потребителю ВЗ — 70 единиц.. Поставщик A3 должен доставить груз только потребителю В1 в количестве 90 ед. Поставщик A3 должен доставить груз только потребителю В1 в количестве 110 ед.

Возможно эта страница вам будет полезна:

Линейное программирование в Excel

Модели целочисленного линейного программирования

При рассмотрении целого ряда экономических задач линейного программирования необходимо учитывать требование получения целочисленного решения. Такие задачи называются задачами целочисленного программирования .

Принципиальное отличие задачи целочисленного линейного программирования от обычной ЗЛП состоит только в том, что в системе ограничений вводится дополнительное ограничение па целочисленность переменных, т.е. задача целочисленного линейного программирования формулируется следующим образом: найти максимум или минимум функции

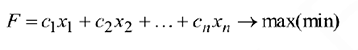
при ограничениях

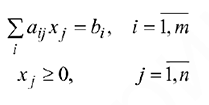
а также дополнительном ограничении:

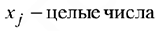
Для решения задач целочисленного программирования используют метод Гомори (метод отсечений) и метод ветвей и границ.

Идея метода Гомори состоит в том, что сначала задача решается без условия целочисленности. Если полученное решение целочисленное, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами: оно должно быть линейным;

должно отсекать найденный оптимальный нецелочисленный план;

• не должно отсекать ни одного целочисленного плана. Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением.

Далее задача решается с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и т.д.

Алгоритм метода Гомори

• С помощью симплекс-метода находят решение задачи (9.1) — (9.3) без учета требования целочисленности переменных. Если полученное решение целочисленное, то задача (9.1) — (9.4) решена. Если задача (9.1) -(9.3) неразрешима (т.е. не имеет конечного оптимума или условия ее противоречивы), то и задача (9.1) — (9.4) также неразрешима.
• Если полученное решение нецелочисленное, то составляют дополнительное ограничение для переменной, которая в оптимальном плане задачи (9.1)—(9.3) имеет максимальную дробную часть, а в оптимальном плане задачи (9.1)—(9.4) должна быть целочисленной. Для составления дополнительного ограничения используется последняя симплекс-таблица. Ограничение имеет вид:

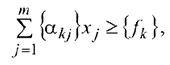
где 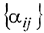— дробная часть коэффициента при переменной 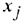в 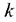— той строке последней симплексной таблицы, 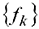— дробная часть значения базисной переменной .

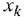• Неравенство (9.5) заменяют уравнением путем ввода дополнительной переменной и добавляют его к ранее решенной задаче, получают новую задачу. Решают ее симплексным методом, если оптимальный план новой задачи целочисленный, то исходная задача решена. В противном случае составляется новое дополнительное ограничение и т.д., пока не будет получено целочисленное решение задачи.

Возможно эта страница вам будет полезна:

Курсовая работа по линейному программированию

Задача №9.1.

На приобретение оборудования (станков) для участка цеха выделены 30 т. р. Производственная площадь участка — 70 м2. Имеется возможность закупить станки двух видов: стоимостью 5 т. р. и 3 т. р. Станок первого вида требует для установки 12 м2 и дает продукции на 8 т. р. в месяц. Станок второго вида требует 6 м» площади и дает продукции на 2 т. р. в месяц. Определить оптимальный план приобретения оборудования, при котором производительность участка цеха в месяц была бы максимальной.

Решение:

• Составим математическую модель задачи:

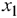— количество станков первого вида;

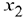— количество станков второго вида;

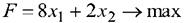
целевая функция (производительность участка в месяц в ден. ед.).

Система ограничений:

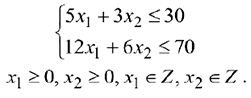
• С помощью симплекс-метода найдем решение задачи без учета требования целочисленности переменных. Для этого приведем задачу к каноническому виду, т.е. в системе ограничений введем две дополнительные переменные 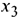и :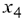

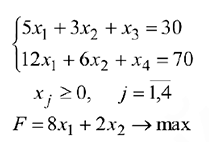
В качестве базисных переменных можем взять дополнительные переменные 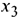и .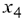

Составим симплексную таблицу (табл. 9.1):

I шаг.

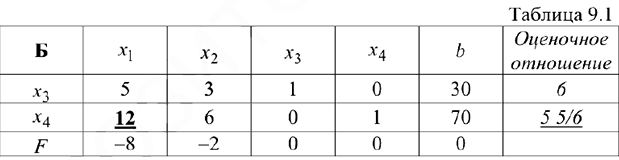
Полученное на I шаге базисное решение (опорный план) не является оптимальным, т.к. в индексной строке есть отрицательные коэффициенты.

В качестве разрешающего выберем столбец, соответствующий переменной 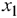, т.к. ей соответствует наибольший по модулю отрицательный коэффициент (-8).

Вычислим оценочные отношения для строк соответствующих базисным переменным.

Вторая строка (соответствующая базисной переменной 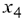) является разрешающей (ей соответствует минимальное оценочное отношение 5,8).

Разрешающий элемент 12, который находится на пересечении разрешающего столбца и разрешающей строки.

II шаг.

Производим пересчет симплекс-таблицы (в табл. 9.2 приведён конечный результат).

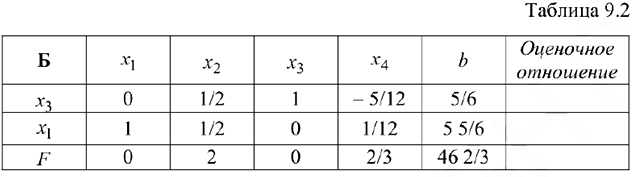
Полученный опорный план

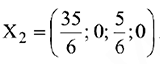
является оптимальным, т.к. индексная строка не содержит отрицательных элементов.

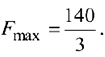
Полученное решение нецелочисленное, поэтому составим дополнительное ограничение для переменной 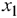, которая в оптимальном плане задачи должна быть целочисленной. Для составления дополнительного ограничения воспользуемся последней симплекс-таблицей. Выпишем уравнение, содержащее неизвестную :

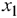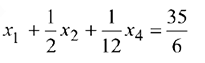
Дополнительное ограничение будет иметь вид:

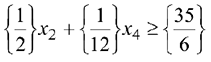
(фигурные скобки обозначают дробную часть числа).

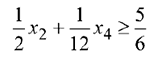
С помощью дополнительной переменной преобразуем данное неравенство в уравнение:

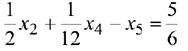
и присоединим его к исходной системе ограничений, получим новую задачу. Для ее решения в последнюю симплекс-таблицу исходной задачи добавляем строку, соответствующую введенному ограничению (табл. 9.3).

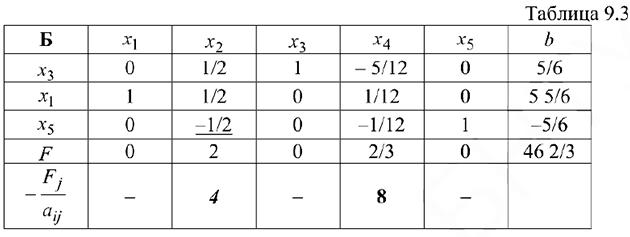
План

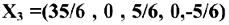
недопустим, так как -5/6 < 0, зато 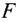-строка (0, 2, 0, 2/3, 0) не содержит отрицательных чисел. Это означает, что пашу задачу можно решить двойственным симплекс методом.

При решении задачи двойственным симплекс методом за разрешающую принимается строка с максимальным по абсолютной величине отрицательным 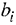. У нас это строка 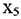. За разрешающий принимается столбец с минимальным значением- 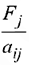, где а 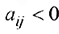(столбец 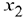). Разрешающий элемент выделяем в таблице (см. табл. 9.3) и делаем для него шаг Жордана-Гаусса:

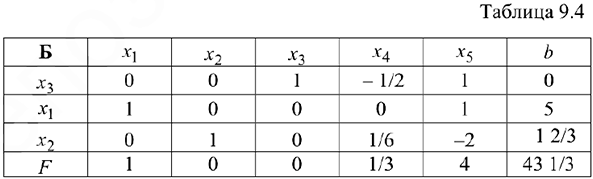
План

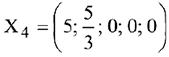
оптимален, но переменная 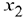не является целочисленной. Введем второе дополнительное ограничение, для этого из последней симплексной таблицы выпишем последнее уравнение:

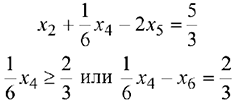
Это ограничение добавляем в последнюю симплексную таблицу и решаем новую задачу двойственным симплекс-методом.

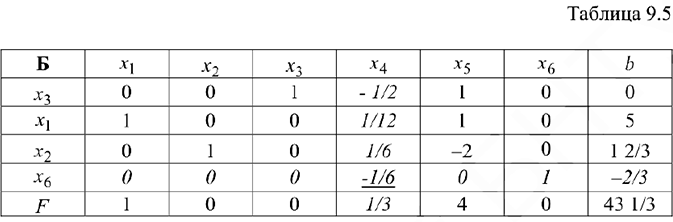
За разрешающую принимаем строку с максимальным по абсолютной величине отрицательным 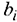. У нас это строка 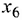. За разрешающий принимается столбец с минимальным значением—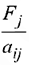. где 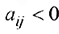(столбец 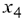). Разрешающий элемент выделяем в таблице (см. табл. 9.5) и делаем для него шаг Жордана-Гаусса:

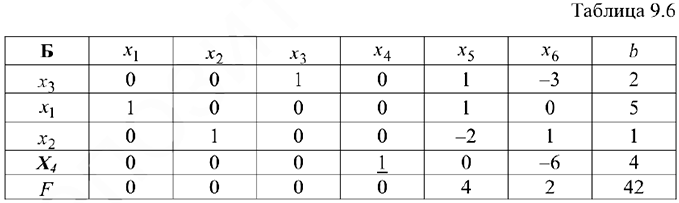
План

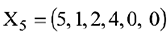
оптимален и является целочисленным, следовательно, оптимальное решение исходной задачи имеет вид:

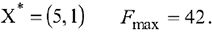
Решение задачи целочисленной оптимизации в Microsoft Excel осуществляется командой Поиск решения из меню Данные. Но при решении целочисленных задач необходимо в форму представления данных ввести требование целочисленности переменных.

Вводим данные в таблицу Excel, как представлено на рисунке 9.1

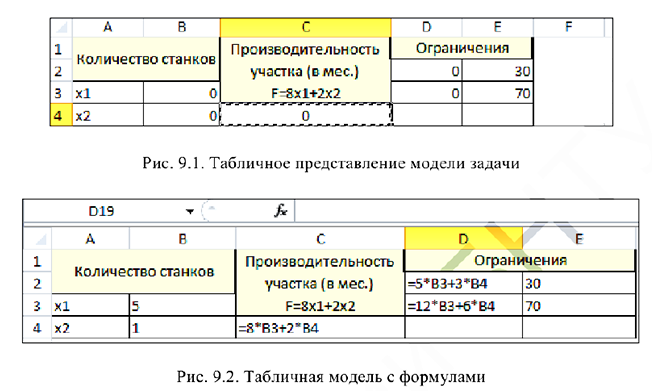
Вызываем диалоговое окно Поиск решения и заносим в этом окне необходимые данные (рис. 9.3)

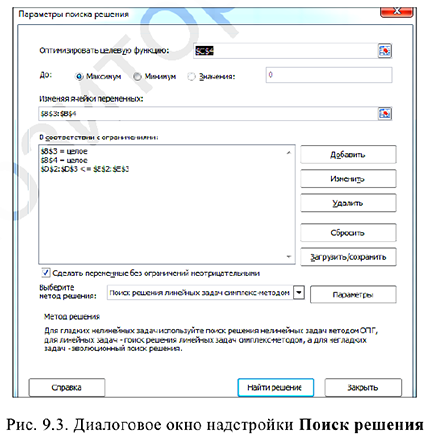
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.

Метод ветвей и границ

Задача №9.2.

Методом ветвей и границ решить задачу

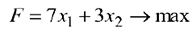
при ограничениях

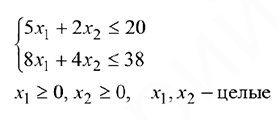
Решение:

Найдём оптимальное решение этой задачи как непрерывной (симплекс-методом).

Сначала приведем исходную (основную) задачу к каноническому виду. Очевидно, что для получения канонического вида необходимо прибавить 2 дополнительные неотрицательные переменные 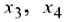соответственно к первому и второму неравенствам системы ограничений.

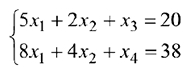
Поэтому можно сразу обратиться к таблице Гаусса (табл.9.1) и заполнить соответствующие блоки.

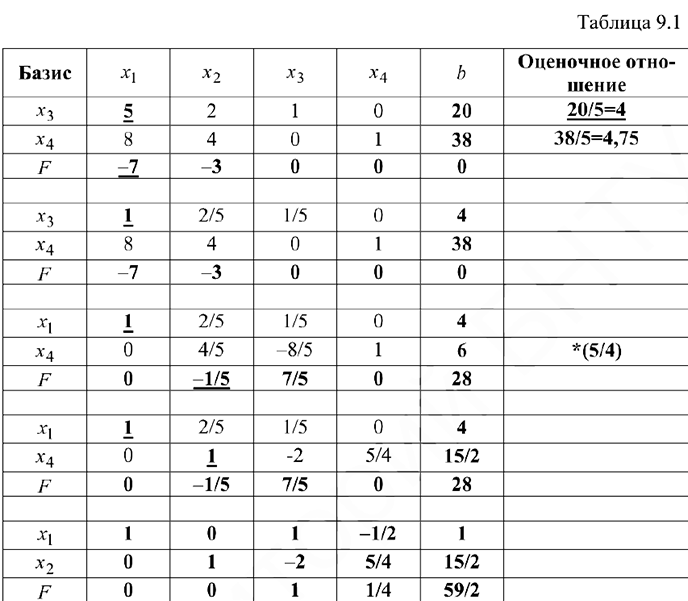
Оптимальное решение задачи:

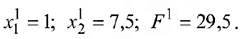
Верхний индекс у переменных соответствует номеру задачи.

В полученном решении 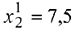не удовлетворяет требованиям цело-численности.

В связи с этим для дальнейшего решения составим задачи с граничными условиями, исключающими возможность получения нецелочисленного значения 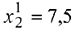. Такими граничными условиями являются

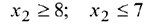
Граничное условие 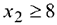входит в Задачу 2, решение которой найдём в Excel, используя надстройку «.Поискрешения».

• Создадим таблицу для ввода исходных данных: переменных, целевой функции,ограничений.
• Введем начальные нулевые значения для 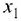и .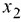
• Зададим целевую функцию в ячейке F3 и ограничения в ячейках Е6, Е7 и Е8 (рис. (9.5).

Далее для исключения получения нецелочисленного значения

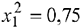
введём дополнительные граничные условия и решим последовательно две задачи: Задачу 3-е условиями

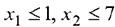
и Задачу 4-е условиями

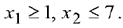
Решения этих задач представлены, соответственно, на рис. 9.8 и рис. 9.9.

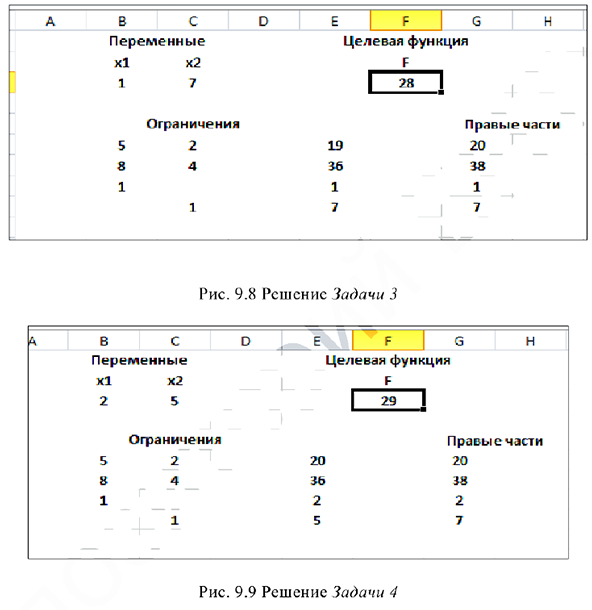
Схема решения всех этих задач приведена на рис. 9.10, а результат решения — в таблице 2

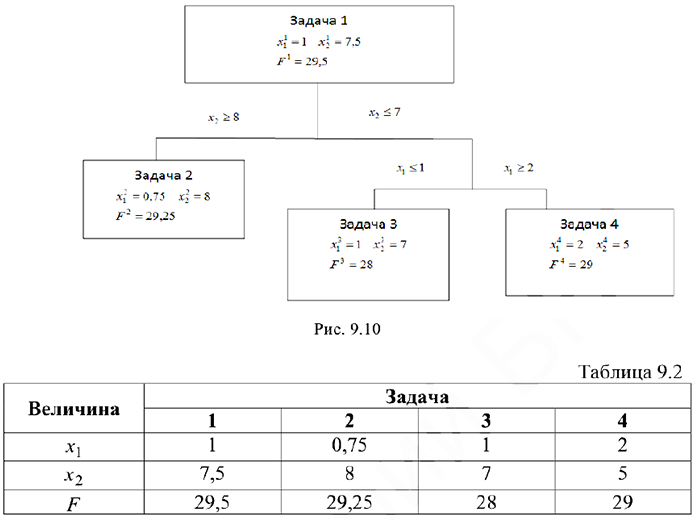
Из таблицы 2 видно, что решение Задачи 3 наиболее близкое к непрерывному по значениям переменных (см. таблицу 1), не является оптимальным. Оптимальным же является решение Задачи 4, в котором значения переменных существенно отличаются от непрерывного решения. Приведённый пример наглядно показывает, что округление оптимального решения непрерывной задачи может не обеспечить получения оптимального решения целочисленной задачи.