Оглавление:

| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как получить помощь в выполнении заданий по математическому программированию
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько стоит помощь
Стоимость помощи зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения
Минимальный срок выполнения составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения действует гарантия. В течении 1 года я и моя команда исправим любые ошибки.
Чуть ниже я предоставила теорию с практикой, чтобы вы освежили знания и примеры оформления заказов по некоторым темам математического программирования, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.
Решение систем линейных уравнений методом Жордана-Гаусса
Системой линейных алгебраических уравнений называется совокупность формальных равенств вида:
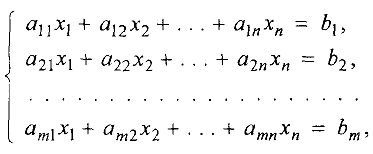
где 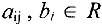 — заданные числа,
— заданные числа, 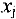 — неизвестные,
— неизвестные, 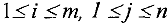 .
.
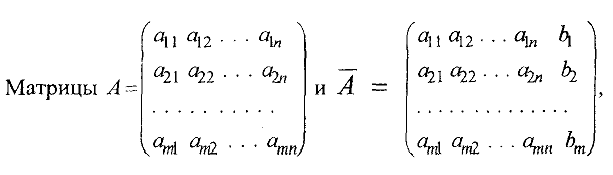
называются соответственно матрицей системы и расширенной матрицей системы.
Решением системы (1) называется упорядоченная совокупность чисел 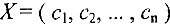 , которые при подстановке
, которые при подстановке 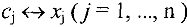 обращают каждое уравнение системы (1) в верное равенство. Система, имеющая хотя бы одно решение, называется совместной, иначе — несовместной. Решить систему — означает найти все ее решения. Две системы называются эквивалентными или равносильными, если они имеют одинаковые множества решений. Аналогично, расширенные матрицы эквивалентных систем будем называть эквивалентными.
обращают каждое уравнение системы (1) в верное равенство. Система, имеющая хотя бы одно решение, называется совместной, иначе — несовместной. Решить систему — означает найти все ее решения. Две системы называются эквивалентными или равносильными, если они имеют одинаковые множества решений. Аналогично, расширенные матрицы эквивалентных систем будем называть эквивалентными.
Например, системы
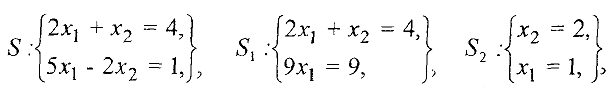
с расширенными матрицами
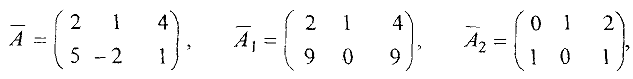
являются эквивалентными, так как все они имеют единственное решение 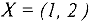 .
.
Элементарными преобразованиями матрицы называются: перестановка местами любых двух строк; умножение строки на любое, отличное от нуля число; прибавление к одной строке матрицы любой другой строки, умноженной на любое число; удаление нулевой строки.
Решение системы методом Гаусса и его модификацией — методом Жордана-Гаусса основано на следующем утверждении: матрица, полученная элементарными преобразованиями расширенной матрицы системы эквивалентна исходной матрице, т.е. элементарные преобразования расширенной матрицы системы не изменяют множества решений системы.
Суть обоих методов состоит в том, чтобы при помощи элементарных преобразований привести расширенную матрицу системы к наиболее простому виду, т.е. к такому виду, когда решение найти достаточно легко. Например, ясно, что систему 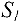 с матрицей
с матрицей 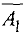 решить легче, чем исходную систему
решить легче, чем исходную систему 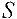 с матрицей
с матрицей 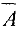 , а решение системы
, а решение системы 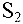 вообще очевидно. Переход от матрицы
вообще очевидно. Переход от матрицы 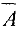 к матрице
к матрице 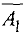 можно осуществить, например, прибавляя ко второй строке матрицы
можно осуществить, например, прибавляя ко второй строке матрицы 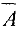 , первой строки, умноженной на 2. Чтобы из матрицы
, первой строки, умноженной на 2. Чтобы из матрицы 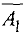 получить
получить 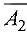 , можно поступить следующим образом: сначала вторую строку
, можно поступить следующим образом: сначала вторую строку 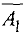 умножим на 1/9. а затем к первой строке прибавим вторую, умноженную на -2.
умножим на 1/9. а затем к первой строке прибавим вторую, умноженную на -2.
Переменная 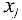 называется базисной в
называется базисной в 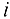 -м уравнении системы (1) если
-м уравнении системы (1) если
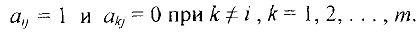
Другими словами, переменная 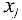 является базисной в
является базисной в 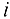 -м уравнении, если коэффициент при ней в этом уравнении равен 1, а в остальных уравнениях — 0, т.е. в других уравнениях этой переменной нет.
-м уравнении, если коэффициент при ней в этом уравнении равен 1, а в остальных уравнениях — 0, т.е. в других уравнениях этой переменной нет.
Говорят, что матрица системы приведена к базисному виду (или имеет базис) если в каждом ее уравнении имеется базисная переменная. Например, матрица  системы
системы  не имеет ни одной базисной переменной, матрица
не имеет ни одной базисной переменной, матрица 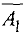 имеет базисную переменную х2 в первом уравнении, а матрица
имеет базисную переменную х2 в первом уравнении, а матрица 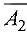 приведена к базисному виду.
приведена к базисному виду.
Справедливо следующее утверждение: При помощи элементарных преобразований расширенную матрицу любой совместной системы можно привести к базисному виду.
Если матрица системы приведена к базисному виду, то переменные, не являющиеся базисными, называются свободными. Например, в матрице 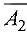 все переменные — базисные, свободных нет.
все переменные — базисные, свободных нет.
Решение системы, полученное после приравнивания нулю всех свободных переменных, называется базисным.
Алгоритм приведения матрицы к базисному виду
Каждая итерация алгоритма состоит из трех шагов:
Шаг . В первой строке матрицы находим ненулевой элемент 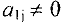 , (желательно,
, (желательно, 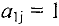 ) . Если таких нет, то в случае
) . Если таких нет, то в случае 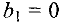 вычеркиваем нулевую строку; если
вычеркиваем нулевую строку; если 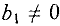 , то, очевидно, система несовместна. Найденный элемент назовем разрешающим (или ведущим).
, то, очевидно, система несовместна. Найденный элемент назовем разрешающим (или ведущим).
Если 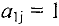 то переходим к шагу 3. иначе к шагу 2.
то переходим к шагу 3. иначе к шагу 2.
Шаг 2. Делим первую строку на разрешающий элемент 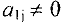 .
.
(После этого шага коэффициент при xt в первом уравнении будет 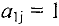 ).
).
Шаг 3. Ко всем остальным строкам, кроме первой, прибавляем первую строку, умноженную на 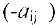 , где
, где 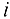 — номер изменяемой строки
— номер изменяемой строки 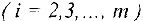 . После этого шага коэффициент при
. После этого шага коэффициент при 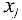 в остальных уравнениях будет 0 , и неременная
в остальных уравнениях будет 0 , и неременная 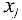 станет базисной в первом уравнении. Затем применяем шаги 1 , 2 и 3 ко второму уравнению полученной матрицы и т.д. Так как число уравнений системы конечно, то этот процесс завершится не более чем за m итераций.
станет базисной в первом уравнении. Затем применяем шаги 1 , 2 и 3 ко второму уравнению полученной матрицы и т.д. Так как число уравнений системы конечно, то этот процесс завершится не более чем за m итераций.
Решение системы по этому алгоритму называется методом Жордана-Гаусса.
После того, как система приведена к базисному виду, находят базисное решение, соответствующее выбранному базису. Для этого переменные, не вошедшие в базис, приравнивают нулю, а остальные переменные (базисные) находят но правым частям соответствующих уравнений. Приведем решение типового примера задания 1: Найти базисное решение системы с расширенной матрицей
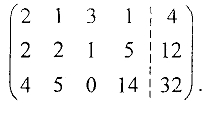
Применим алгоритм приведения матрицы к базисному виду: В первой строке элемент 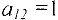 , поэтому выберем его в качестве разрешающего. Теперь изменяем вторую и третью строки следующим образом: ко второй строке прибавляем первую, умноженную на (-2). к третьей прибавляем первую, умноженную на (-5). В результате получим матрицу
, поэтому выберем его в качестве разрешающего. Теперь изменяем вторую и третью строки следующим образом: ко второй строке прибавляем первую, умноженную на (-2). к третьей прибавляем первую, умноженную на (-5). В результате получим матрицу
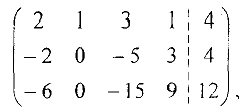
в которой переменная 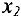 стала базисной в первом уравнении. Теперь применяем шаги 1-3 ко второй строке полученной матрицы. Находим ненулевой элемент, например,
стала базисной в первом уравнении. Теперь применяем шаги 1-3 ко второй строке полученной матрицы. Находим ненулевой элемент, например, 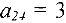 и делим вторую строку на этот элемент. Получим матрицу
и делим вторую строку на этот элемент. Получим матрицу
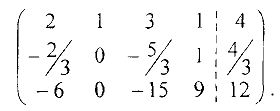
Теперь делаем нули в остальных строках четвертого столбца этой матрицы, для чего к первой строке прибавляем вторую, умноженную на -1, к третьей прибавляем вторую, умноженную на -9. В результате расширенная матрица системы примет вид:
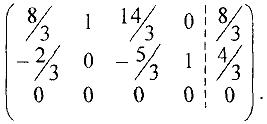
Вычеркивая нулевую третью строку, получим матрицу, в базисном виде:
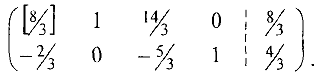
В первой строке базисной является переменная  , а во второй -переменная
, а во второй -переменная 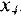 . Переменные
. Переменные 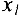 и
и 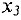 являются свободными. Приравнивая их нулю, получаем базисное решение, соответствующее этому базису:
являются свободными. Приравнивая их нулю, получаем базисное решение, соответствующее этому базису:
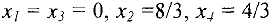
или
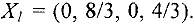
Найдем другое базисное решение, т.е. решение, в котором базисными являются другие переменные. В базис можно включить переменные 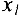 или
или 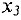 , которые сейчас являются свободными. Выберем, например, переменную
, которые сейчас являются свободными. Выберем, например, переменную 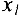 для включения в базис. Ее можно сделать базисной в первой строке, т.к. элемент
для включения в базис. Ее можно сделать базисной в первой строке, т.к. элемент
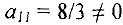
(при этом из базиса выйдет переменная  ), или во второй строке
), или во второй строке
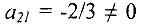
(при этом из базиса выйдет 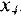 ). Будем делать
). Будем делать 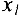 базисной, например, в первой строке, т.е. в качестве разрешающего выберем элемент
базисной, например, в первой строке, т.е. в качестве разрешающего выберем элемент 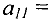
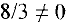 (помечен в последней матрице). Как и раньше, разделив первую строку на разрешающий элемент и прибавив ко второй строке полученную первую, умноженную на 2/3, приведем матрицу к новому базису:
(помечен в последней матрице). Как и раньше, разделив первую строку на разрешающий элемент и прибавив ко второй строке полученную первую, умноженную на 2/3, приведем матрицу к новому базису:
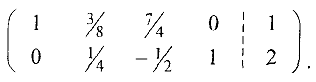
Полагая свободные переменные 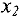 и
и 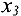 равными нулю, получим новое базисное решение
равными нулю, получим новое базисное решение 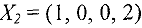 .
.
Возможно эта страница вам будет полезна:
| Предмет математическое программирование |
Решение задачи математического программирования геометрическим методом
Общей задачей линейного программирования называется задача нахождения минимума (максимума) линейной функции
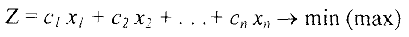
при ограничениях :
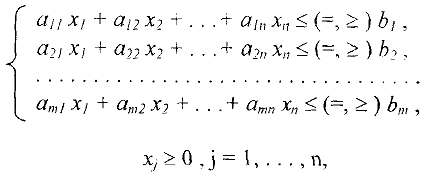
где 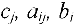 — заданные числа,
— заданные числа, 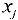 — неизвестные,
— неизвестные, 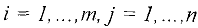 и в любом из ограничений вида (2) может встречаться любой из знаков
и в любом из ограничений вида (2) может встречаться любой из знаков 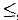 или
или 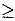 .
.
Если число неизвестных 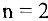 , то задача (1) — (3) примет вид
, то задача (1) — (3) примет вид
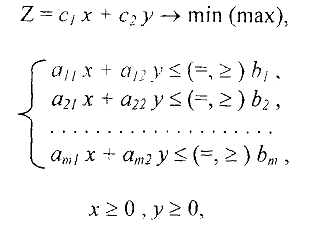
и ее можно решить геометрическим методом, так как каждая пара неизвестных 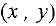 может быть представлена точкой на координатной плоскости
может быть представлена точкой на координатной плоскости 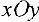 .
.
При решении задачи (4) — (6) сначала строят так называемую допустимую область, т.е. множество точек 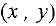 плоскости, координаты которых удовлетворяют всем ограничениям (5) и лежат в первой четверти координатной плоскости (ограничение (6)). Поскольку все ограничения (5) — линейные, то допустимая область будет представлять собой выпуклый многоугольник (конечный или бесконечный) или пустое множество.
плоскости, координаты которых удовлетворяют всем ограничениям (5) и лежат в первой четверти координатной плоскости (ограничение (6)). Поскольку все ограничения (5) — линейные, то допустимая область будет представлять собой выпуклый многоугольник (конечный или бесконечный) или пустое множество.
Затем среди точек допустимой области находят оптимальную, т.е. такую точку 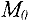 координаты которой
координаты которой 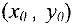 доставляют минимум (максимум) целевой функции
доставляют минимум (максимум) целевой функции 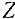 . Для этого по виду целевой функции (4) строят линию уровня функции
. Для этого по виду целевой функции (4) строят линию уровня функции 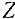 , соответствующую
, соответствующую 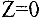 , т.е. прямую
, т.е. прямую 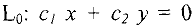 и находят градиент функции
и находят градиент функции
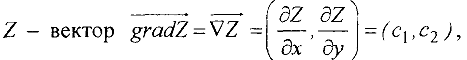
который показывает направление наибыстрейшего возрастания функции 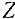 . Вектор антиградиента
. Вектор антиградиента 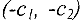 будет показывать направление наибыстрейшего убывания целевой функции
будет показывать направление наибыстрейшего убывания целевой функции 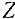 . Вектор градиента перпендикулярен линии уровня
. Вектор градиента перпендикулярен линии уровня 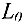 .
.
Перемещая линию уровня 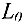 параллельно самой себе в направлении градиента
параллельно самой себе в направлении градиента 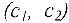 , находим последнюю точку допустимой области, которую она пересекает при таком движении. Очевидно, что это будет точка максимума. Перемещая линию уровня в противоположном направлении
, находим последнюю точку допустимой области, которую она пересекает при таком движении. Очевидно, что это будет точка максимума. Перемещая линию уровня в противоположном направлении 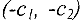 , находим точку минимума. Поясним этот метод на конкретном примере.
, находим точку минимума. Поясним этот метод на конкретном примере.
Пример оформления заказа №1.
Геометрическим методом найти максимум и минимум функции 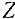 для
для 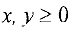 при заданных ограничениях
при заданных ограничениях
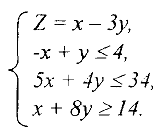
Решение:
Построим допустимую область. Для этого в системе координат  строим прямую
строим прямую 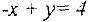 — границу первого ограничения. Затем определяем, в какой полуплоскости находятся точки
— границу первого ограничения. Затем определяем, в какой полуплоскости находятся точки 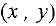 , для которых
, для которых 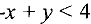 . Для этого выбираем любую точку, например (0, 0), и проверяем, удовлетворяет ли она этому неравенству. Поскольку -0 + 0 = 0 < 4, то точки, для которых
. Для этого выбираем любую точку, например (0, 0), и проверяем, удовлетворяет ли она этому неравенству. Поскольку -0 + 0 = 0 < 4, то точки, для которых 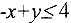 лежат в той же полуплоскости, что и точка
лежат в той же полуплоскости, что и точка 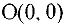 , т.е. справа (ниже) от границы
, т.е. справа (ниже) от границы 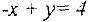 .
.
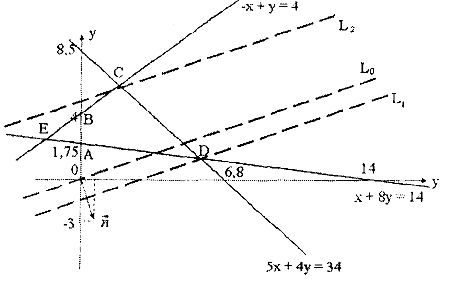
Аналогично строятся остальные полуплоскости, соответствующие ограничениям 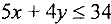 и
и 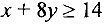 (ниже прямой
(ниже прямой 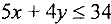 и выше прямой
и выше прямой 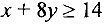 ). Множество точек, удовлетворяющих всем трем неравенствам, образуют треугольник
). Множество точек, удовлетворяющих всем трем неравенствам, образуют треугольник 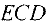 . Учитывая ограничение
. Учитывая ограничение 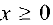 и
и 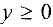 , получаем допустимую область — четырехугольник
, получаем допустимую область — четырехугольник 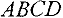 .
.
Проведем линию уровня  , соответствующую значению
, соответствующую значению  , т.е. прямую
, т.е. прямую 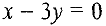 (для точек, лежащих на этой прямой, значение
(для точек, лежащих на этой прямой, значение 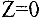 ). Она будет проходить через точку
). Она будет проходить через точку 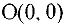 перпендикулярно вектору
перпендикулярно вектору 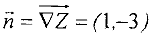 . Перемещая линию уровня в направлении градиента
. Перемещая линию уровня в направлении градиента 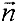 т.е. в направлении возрастания
т.е. в направлении возрастания 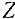 , находим последнюю точку допустимой области, которую линия уровня пересекает при этом движении (линия
, находим последнюю точку допустимой области, которую линия уровня пересекает при этом движении (линия 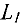 ). Это будет точка максимума. В нашем случае — это точка
). Это будет точка максимума. В нашем случае — это точка 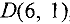 , координаты которой можно найти, решив систему линейных уравнений
, координаты которой можно найти, решив систему линейных уравнений 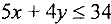 и
и 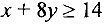 . Аналогично, двигая линию уровня в противоположном направлении до линии
. Аналогично, двигая линию уровня в противоположном направлении до линии 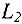 , находим точку минимума — точку
, находим точку минимума — точку 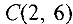 . Таким образом,
. Таким образом,
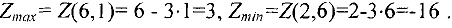
Задача решена полностью.
Решение задачи математического программирования симплекс-методом
Задача линейного программирования (ЗЛГ1) (1) — (3) (см. задание 2) называется канонической, если все ограничения вида (2) являются уравнениями (равенствами), т.е. задачей линейного программирования в канонической форме называется задача:
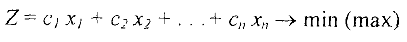
при ограничениях :
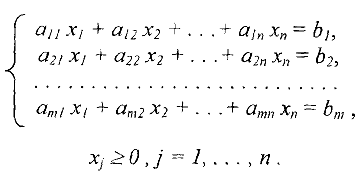
Симплекс-метод является вычислительной процедурой, которая позволяет решить любую каноническую ЗЛП алгебраическим методом. Теоретической основой метода являются следующие два утверждения:
Теорема 1. Если ЗЛП имеет допустимые решения, то существует хотя бы одно базисное допустимое решение задачи.
Теорема 2. Если ЗЛП имеет конечное оптимальное решение, то хотя бы одно из оптимальных решений является базисным.
Напомним, что решение системы (2) называется допустимым, если оно удовлетворяет ограничениям (3). Таким образом, из теоремы 1 следует, что если не существует ни одного базисного допустимого решения системы (2), то эта система вообще не имеет допустимых решений, т.е. ограничения (2) — (3) являются несовместными. В случае если имеются допустимые решения системы 2, то теорема 2 утверждает, что оптимальное решение ЗЛП можно найти среди базисных допустимых решений этой системы, которых, как мы знаем, конечное число. Суть симплекс-метода и состоит в последовательном переборе базисных допустимых решений системы (2), начиная с некоторого начального, которое еще называют первоначальным опорным планом. Перебор осуществляется таким образом, чтобы каждое новое решение было лучше предыдущего (в смысле приближения к максимуму или минимуму целевой функции 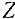 ).
).
Итак, для применения метода необходимо, чтобы задача была в канонической форме, и чтобы существовало начальное базисное допустимое решение (опорный план), наличие которого гарантирует непротиворечивость ограничений задачи.
Чтобы преобразовать ЗЛП к каноническому виду к правой части каждого ограничения-неравенства прибавляют или вычитают неотрицательную дополнительную переменную, например, ограничение
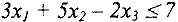
преобразуется в уравнение
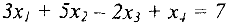
прибавлением дополнительной переменной 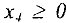 , а неравенство вида
, а неравенство вида
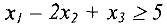
заменяется на уравнение
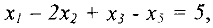
где 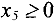 .
.
Заметим, что знак неравенства 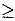 можно заменить на
можно заменить на 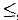 умножением всего неравенства на -1, например, неравенство
умножением всего неравенства на -1, например, неравенство 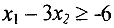 эквивалентно неравенству —
эквивалентно неравенству —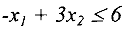 . Отметим также, что максимизацию целевой функции
. Отметим также, что максимизацию целевой функции 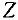 можно заменить на минимизацию функции —
можно заменить на минимизацию функции —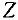 и наоборот, так как максимум функции
и наоборот, так как максимум функции
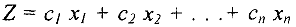
достигается в тех же точках, что и минимум функции
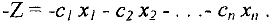
Мы приведем алгоритм симплекс-метода для минимизации целевой функции (1)
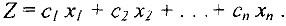
Поясним суть метода на следующем примере:
Пусть требуется решить следующую ЗЛП: Найти максимум функции
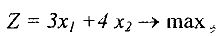
при ограничениях:
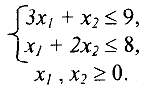
Приведем задачу к каноническому виду и заменим максимизацию целевой функции 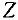 на минимизацию функции
на минимизацию функции 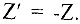 Получим следующую задачу.
Получим следующую задачу.
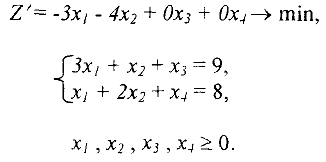
Ясно, что переменные 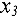 и
и 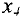 являются базисными в системе (5) и соответствующее базисное решение
являются базисными в системе (5) и соответствующее базисное решение 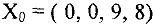 является допустимым, т.к. все
является допустимым, т.к. все 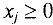 . При этом
. При этом 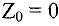 .
.
Начнем с того, что проверим опорный план 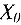 на оптимальность. Поскольку целевая функция
на оптимальность. Поскольку целевая функция
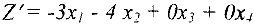
выражена через свободные переменные 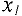 и
и 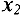 , коэффициенты при которых отрицательны, то, очевидно, увеличение этих переменных приведет к уменьшению значения целевой функции на 3 ед. при увеличении
, коэффициенты при которых отрицательны, то, очевидно, увеличение этих переменных приведет к уменьшению значения целевой функции на 3 ед. при увеличении 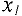 на одну единицу и на 4 ед. при увеличении на одну единицу
на одну единицу и на 4 ед. при увеличении на одну единицу 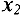 (сейчас
(сейчас 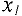 и
и 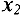 равны 0 ). Поэтому делаем вывод, что опорный план
равны 0 ). Поэтому делаем вывод, что опорный план 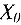 не является оптимальным (т.к. введение в базис переменных
не является оптимальным (т.к. введение в базис переменных 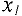 и
и 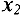 приведёт к уменьшению значения целевой функции).
приведёт к уменьшению значения целевой функции).
Итак, для того, чтобы получить лучшее базисное решение, мы должны включить в базис переменные 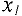 и
и 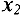 . Будем вводить их в базис по очереди. Поскольку увеличение переменной
. Будем вводить их в базис по очереди. Поскольку увеличение переменной 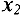 быстрее уменьшает
быстрее уменьшает 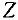 , то выбираем переменную
, то выбираем переменную 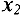 для включения ее в базис (это разумно, но не обязательно). Теперь надо выяснить в какой строке системы (5) переменная
для включения ее в базис (это разумно, но не обязательно). Теперь надо выяснить в какой строке системы (5) переменная 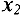 будет базисной, чтобы полученное новое базисное решение было допустимым.
будет базисной, чтобы полученное новое базисное решение было допустимым.
Анализируя первое уравнение системы
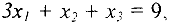
замечаем, что поскольку 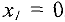 , то увеличение
, то увеличение 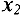 влечет уменьшение
влечет уменьшение 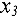 . Так как
. Так как 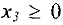 ввиду (6), то увеличение
ввиду (6), то увеличение 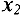 возможно лишь до тех пор, пока
возможно лишь до тех пор, пока 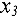 не уменьшится до нуля, т.е. до значения 9/1 = 9. Поскольку переменная
не уменьшится до нуля, т.е. до значения 9/1 = 9. Поскольку переменная 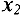 есть также и во втором уравнении, то рассуждая аналогично, заключаем, что в этом случае переменную
есть также и во втором уравнении, то рассуждая аналогично, заключаем, что в этом случае переменную 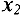 можно увеличивать максимум до значения 8/2 = 4 при котором переменная
можно увеличивать максимум до значения 8/2 = 4 при котором переменная 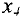 уменьшится до нуля.
уменьшится до нуля.
Новое базисное решение будет допустимым, если мы будем увеличивать переменную 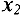 до значения, равного
до значения, равного 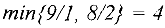 , которое достигается во второй строке системы. Поэтому переменная
, которое достигается во второй строке системы. Поэтому переменная 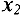 должна быть базисной во втором уравнении, элемент
должна быть базисной во втором уравнении, элемент 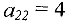 системы будет разрешающим и, проводя преобразования Жордана-Гаусса, получаем новое (улучшенное) базисное допустимое решение:
системы будет разрешающим и, проводя преобразования Жордана-Гаусса, получаем новое (улучшенное) базисное допустимое решение:
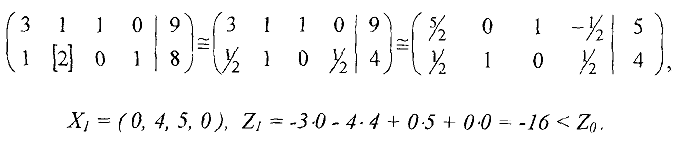
Теперь повторим эту процедуру для нового опорного плана 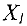 . Для того, чтобы проверить его на оптимальность, нужно выразить целевую функцию через свободные переменные
. Для того, чтобы проверить его на оптимальность, нужно выразить целевую функцию через свободные переменные 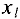 и
и 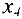 этого плана, поскольку их нужно будет изменять, чтобы получить другое (лучшее) базисное решение. Для этого из второго уравнения последней системы выражаем базисную переменную
этого плана, поскольку их нужно будет изменять, чтобы получить другое (лучшее) базисное решение. Для этого из второго уравнения последней системы выражаем базисную переменную
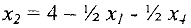
и подставляем ее в целевую функцию
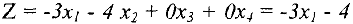
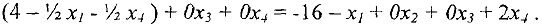
Проводимые вычисления удобно оформлять в виде так называемых симплекс-таблиц, которые являются, фактически, расширенными матрицами системы ограничений (5) с добавленной  — строкой.
— строкой.
Исходная симплекс-таблица.
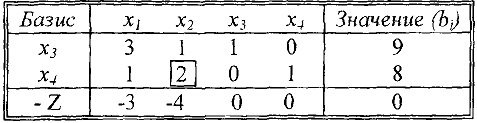
Опорный план
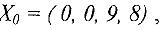
значение 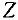 равно
равно 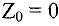 .
.
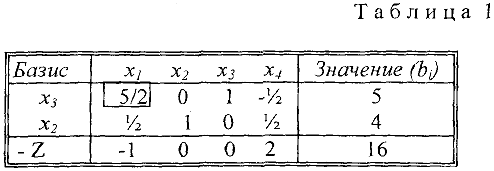
План
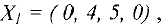
значение 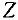 равно
равно 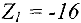 .
.
Последняя строка симплекс-таблицы называется 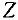 — строкой поскольку в ней расположены коэффициенты целевой функции
— строкой поскольку в ней расположены коэффициенты целевой функции 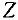 Заметим, что для того, чтобы выразить коэффициенты целевой функции через свободные переменные, достаточно преобразованиями Жордана — Гаусса сделать нули в базисных столбцах
Заметим, что для того, чтобы выразить коэффициенты целевой функции через свободные переменные, достаточно преобразованиями Жордана — Гаусса сделать нули в базисных столбцах 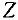 — строки. При этом новое значение
— строки. При этом новое значение 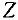 автоматически появится в столбце «Значение» с противоположным знаком.
автоматически появится в столбце «Значение» с противоположным знаком.
Поскольку в 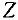 — строке есть отрицательный коэффициент в первом столбце, то план
— строке есть отрицательный коэффициент в первом столбце, то план 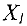 не оптимален, так как введение в базис свободной переменной уменьшает
не оптимален, так как введение в базис свободной переменной уменьшает 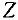 (введение в базис свободной переменной
(введение в базис свободной переменной 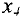 увеличивает
увеличивает 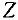 ). Поэтому вводим в базис
). Поэтому вводим в базис 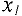 , и первый столбец таблицы будет разрешающим. Чтобы выбрать разрешающую строку, как и раньше делим элементы столбца «Значение» на положительные элементы разрешающего столбца и находим минимальное частное:
, и первый столбец таблицы будет разрешающим. Чтобы выбрать разрешающую строку, как и раньше делим элементы столбца «Значение» на положительные элементы разрешающего столбца и находим минимальное частное:
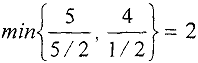
которое достигается в первой строке, которая и будет разрешающей. Значит разрешающим элементом табл. 1 будет элемент 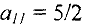 (выделим его прямоугольником). Теперь проведем обычные преобразования Жордана — Гаусса относительно этого элемента, т.е. сначала делим разрешающую строку на разрешающий элемент,
(выделим его прямоугольником). Теперь проведем обычные преобразования Жордана — Гаусса относительно этого элемента, т.е. сначала делим разрешающую строку на разрешающий элемент,
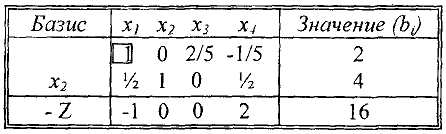
а затем делаем нули на месте всех остальных элементов разрешающего столбца, для чего: ко второй строке прибавляем первую, умноженную на 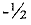 , к
, к 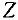 — строке прибавляем первую. В результате получим новую таблицу
— строке прибавляем первую. В результате получим новую таблицу
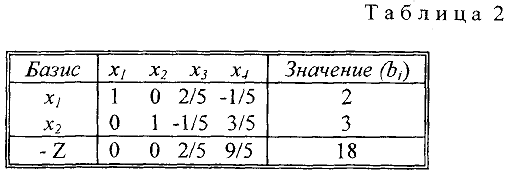
Новое базисное решение (план)
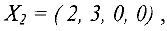
значение 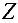 равно
равно 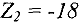 .
.
Просматривая 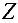 — строку, замечаем, что в ней нет отрицательных элементов. Это означает, что при попытке ввести в базис свободные переменные
— строку, замечаем, что в ней нет отрицательных элементов. Это означает, что при попытке ввести в базис свободные переменные 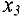 или
или 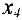 целевая функция будет увеличиваться (на 2/5 и 9/5 единиц при увеличении на 1 единицу переменных
целевая функция будет увеличиваться (на 2/5 и 9/5 единиц при увеличении на 1 единицу переменных 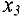 и
и 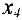 соответственно). Таким образом, других базисных решений, лучших чем
соответственно). Таким образом, других базисных решений, лучших чем 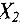 , (т.е. с меньшим, чем -18 значением
, (т.е. с меньшим, чем -18 значением 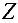 ) не существует.
) не существует.
Решение
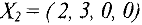
является оптимальным и
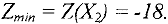
Решение исходной задачи:
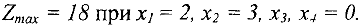
Обобщая приведенные выше рассуждения, сформулируем
Алгоритм Симплекс-метода
Исходные данные: задача в канонической форме; целевая функция минимизируется; найдено начальное базисное допустимое решение (опорный план), то есть система уравнений (2) имеет базис и все правые части уравнений 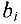 0 — неотрицательны; целевая функция выражена через свободные переменные.
0 — неотрицательны; целевая функция выражена через свободные переменные.
При выполнении этих условий каждая итерация метода состоит из трех шагов:
Шаг 1. Имеющийся план проверяется на оптимальность. Если в 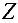 — строке нет отрицательных элементов, то имеющийся план оптимален и задача решена. Если отрицательные элементы есть, то план не оптимален. Выбираем любой отрицательный элемент
— строке нет отрицательных элементов, то имеющийся план оптимален и задача решена. Если отрицательные элементы есть, то план не оптимален. Выбираем любой отрицательный элемент 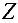 — строки (как правило, максимальный по модулю) и считаем столбец, в котором он находится в качестве разрешающего. Пусть для определенности это столбец переменной
— строки (как правило, максимальный по модулю) и считаем столбец, в котором он находится в качестве разрешающего. Пусть для определенности это столбец переменной 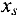 .
.
Шаг 2. Выбор разрешающей строки. Пусть разрешающий столбец, выбранный на предыдущем шаге, это столбец переменной 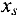 . Для каждой
. Для каждой 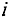 -й строки
-й строки 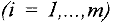 делим элементы столбца свободных членов «Значение» (напомним, что все они неотрицательные) на положительные_элементы разрешающего столбца, стоящие в этой строке, и находим минимальное из полученных частных, т.е. находим
делим элементы столбца свободных членов «Значение» (напомним, что все они неотрицательные) на положительные_элементы разрешающего столбца, стоящие в этой строке, и находим минимальное из полученных частных, т.е. находим
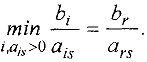
Пусть этот минимум достигается в строке 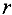 . Тогда
. Тогда 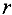 -ая строка является разрешающей, элемент
-ая строка является разрешающей, элемент 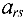 — разрешающий элемент таблицы.
— разрешающий элемент таблицы.
Шаг 3. Пересчет таблицы. Преобразованиями Жордана-Гаусса пересчитываем таблицу относительно разрешающего элемента 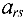 , найденного на предыдущем шаге, для чего:
, найденного на предыдущем шаге, для чего:
3.1. Делим разрешающую строку на разрешающий элемент. В результате, на месте элемента 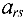 будет стоять
будет стоять 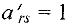 .
.
3.2. Ко всем остальным строкам таблицы (включая 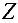 — строку) прибавляем полученную разрешающую, умноженную на элемент
— строку) прибавляем полученную разрешающую, умноженную на элемент 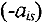 , где
, где 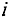 -номер изменяемой строки
-номер изменяемой строки 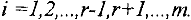 . К
. К 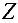 -строке прибавляем разрешающую строку, умноженную на
-строке прибавляем разрешающую строку, умноженную на 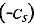 . Иначе говоря, элементы новой таблицы (со штрихом) вычисляю гея по формулам:
. Иначе говоря, элементы новой таблицы (со штрихом) вычисляю гея по формулам:

В результате этих преобразований в столбце xs везде будут стоять нули кроме 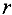 -строки, где будет 1, т.е.
-строки, где будет 1, т.е. 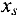 будет новой базисной переменной, целевая функция будет выражена через новые свободные переменные, новый план
будет новой базисной переменной, целевая функция будет выражена через новые свободные переменные, новый план 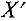 находится в столбце «Значение» и лучше предыдущего, так как значение целевой функции для нового плана равно
находится в столбце «Значение» и лучше предыдущего, так как значение целевой функции для нового плана равно 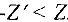 . Переходим к шагу 1 и повторяем всю процедуру для нового плана
. Переходим к шагу 1 и повторяем всю процедуру для нового плана 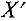 .
.
Поскольку базисных решений системы (2) конечное число, а каждое новое базисное решение лучше предыдущего, то этот процесс завершится за конечное число шагов.
Решение задачи линейного программирования в общем случае. Рассмотрим следующую задачу ЛП:
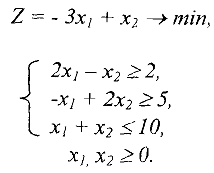
Приведем ее к каноническому виду введением трех неотрицательных переменных 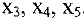 . Получим задачу:
. Получим задачу:
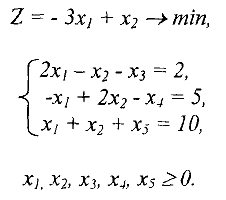
При попытке решить эту задачу симплекс-методом возникает определенная трудность, связанная с тем, что нет очевидного начального базисного допустимого решения (опорного плана), так как переменные 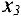 и
и 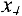 не являются базисными. Умножение первых двух уравнений на -1 также ничего не дает, поскольку соответствующее базисное решение (0, 0, -2, -5, 10) не будет допустимым. Пытаться просто перебирать базисные решения в попытке отыскать допустимое, нецелесообразно, так как неясно, имеет ли эта задача вообще допустимые решения.
не являются базисными. Умножение первых двух уравнений на -1 также ничего не дает, поскольку соответствующее базисное решение (0, 0, -2, -5, 10) не будет допустимым. Пытаться просто перебирать базисные решения в попытке отыскать допустимое, нецелесообразно, так как неясно, имеет ли эта задача вообще допустимые решения.
Для решения проблемы применим метод искусственного базиса. Введем в первые два уравнения (третье не создает проблем) искусственные переменные 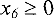 и
и 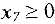 . В результате получим базис из переменных
. В результате получим базис из переменных 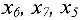 .
.
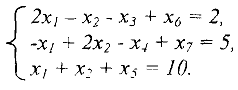
Соответствующее базисное решение 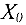 = (0, 0, 0, 0, 10, 2, 5) является допустимым для ограничений (8). Однако ограничения (7) и (8) не являются эквивалентными в том смысле, что любому допустимому решению системы ограничений (8), в котором хотя бы одна искусственная переменная отлична от нуля, нельзя поставить в соответствие допустимое решение системы ограничений (7). С целью исключения искусственных переменных из базисного решения системы ограничений (8), т.е. для получения допустимого базисного решения системы ограничений (7), используем алгоритм симплекс-метода. Для того, чтобы искусственные переменные стали свободными, необходимо, чтобы они были равны нулю (сейчас
= (0, 0, 0, 0, 10, 2, 5) является допустимым для ограничений (8). Однако ограничения (7) и (8) не являются эквивалентными в том смысле, что любому допустимому решению системы ограничений (8), в котором хотя бы одна искусственная переменная отлична от нуля, нельзя поставить в соответствие допустимое решение системы ограничений (7). С целью исключения искусственных переменных из базисного решения системы ограничений (8), т.е. для получения допустимого базисного решения системы ограничений (7), используем алгоритм симплекс-метода. Для того, чтобы искусственные переменные стали свободными, необходимо, чтобы они были равны нулю (сейчас 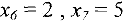 ). Поэтому введем искусственную целевую функцию
). Поэтому введем искусственную целевую функцию
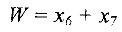
и будем ее минимизировать при ограничениях (8). Если удастся найти базисное допустимое решение при котором 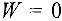 (сейчас
(сейчас 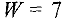 ), то тогда
), то тогда 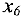 и
и 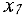 будут равны нулю, поскольку они неотрицательны, и мы получим базис из основных и дополнительных переменных.
будут равны нулю, поскольку они неотрицательны, и мы получим базис из основных и дополнительных переменных.
Таким образом, задача разбивается на два этапа. На первом этапе минимизируется искусственная целевая функция  . Этот этап закончится либо нахождением опорного плана исходной задачи (7), либо тем, что минимизировать функцию
. Этот этап закончится либо нахождением опорного плана исходной задачи (7), либо тем, что минимизировать функцию  до нуля не удастся, т.е. допустимых планов нет, а значит (ввиду теоремы 1) и нет вообще допустимых решений задачи.
до нуля не удастся, т.е. допустимых планов нет, а значит (ввиду теоремы 1) и нет вообще допустимых решений задачи.
Если опорный план найдется, то на втором этапе решаем задачу симплекс-методом. Проиллюстрируем описанный выше метод искусственного базиса, применив его к решению задачи (7).
Этан 1. Составим исходную симплекс-таблицу для задачи (8). Все вычисления будем проводить также и для целевой функции 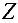 . Тогда после завершения первого этапа получим целевую функцию
. Тогда после завершения первого этапа получим целевую функцию 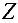 , выраженную через свободные переменные.
, выраженную через свободные переменные.
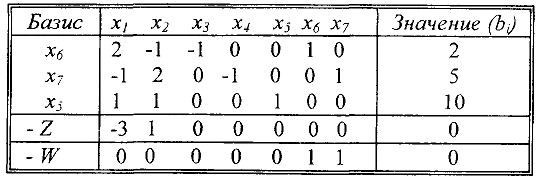
Для того, чтобы начать минимизацию функции 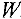 , ее надо выразить через свободные переменные. Для этого, из
, ее надо выразить через свободные переменные. Для этого, из 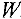 — строки вычтем первую и вторую строки. Получим
— строки вычтем первую и вторую строки. Получим
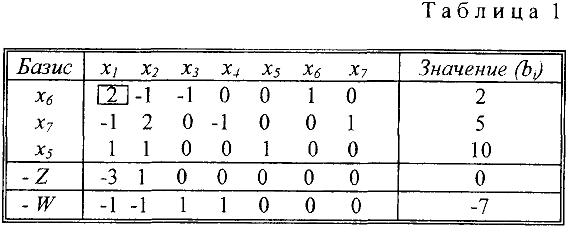
Так как в 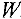 — строке есть отрицательные элементы, то выбираем в качестве разрешающего любой из первых двух столбцов, например первый. Поскольку
— строке есть отрицательные элементы, то выбираем в качестве разрешающего любой из первых двух столбцов, например первый. Поскольку
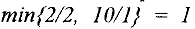
достигается в первой строке, то разрешающая строка — первая и разрешающий элемент  . Пересчитывая таблицу относительно этого элемента, получим новую таблицу:
. Пересчитывая таблицу относительно этого элемента, получим новую таблицу:
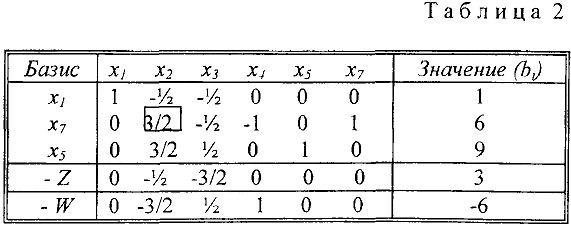
Так как переменная 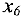 вышла из базиса, то в дальнейшем ее не используем (вычеркиваем столбец
вышла из базиса, то в дальнейшем ее не используем (вычеркиваем столбец 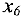 ). Теперь разрешающим столбцом будет второй, разрешающей строкой — вторая и после пересчета получим (поскольку искусственная переменная
). Теперь разрешающим столбцом будет второй, разрешающей строкой — вторая и после пересчета получим (поскольку искусственная переменная 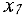 выйдет из базиса, столбец
выйдет из базиса, столбец 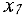 также вычеркиваем):
также вычеркиваем):

Этап 1 успешно завершен, так как искусственные переменные выведены из базиса и мы получили опорный план 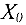 = (3, 4, 0, 0, 3 ) исходной задачи (7), к которому можно применить алгоритм симплекс-метода. На втором этапе
= (3, 4, 0, 0, 3 ) исходной задачи (7), к которому можно применить алгоритм симплекс-метода. На втором этапе 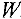 — строка уже не нужна и мы ее вычеркиваем.
— строка уже не нужна и мы ее вычеркиваем.
Этап 2.
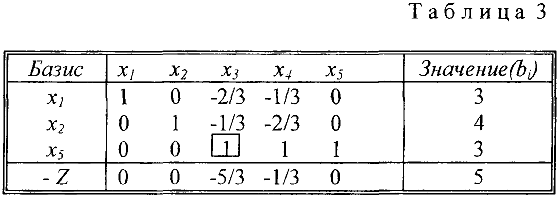
Целевую функцию 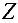 можно уменьшить (сейчас
можно уменьшить (сейчас 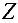 = -5) если ввести в базис
= -5) если ввести в базис 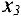 или
или 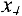 .
.
Выбираем третий столбец в качестве разрешающего, т.к. -5/3 < -1/3. Разрешающей строкой будет третья, т.к. только в ней есть положительный элемент разрешающего столбца. Разрешающий элемент 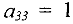 . Пересчитывая таблицу, получим:
. Пересчитывая таблицу, получим:

Поскольку в 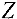 — строке таблицы 4 нет отрицательных элементов, то новый план
— строке таблицы 4 нет отрицательных элементов, то новый план 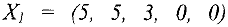 является оптимальным и
является оптимальным и 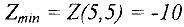 .
.
Задача решена полностью.
Двойственность в математическом программировании. Двойственный симплекс-метод
Рассмотрим задачу линейного программирования в общей форме:
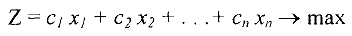
при ограничениях:
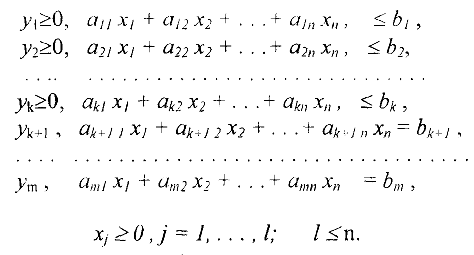
Каждому 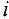 -му ограничению из (2) соответствует переменная
-му ограничению из (2) соответствует переменная 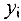 так называемой двойственной задачи к задаче (1) — (3) (показана слева от соответствующего ограничения).
так называемой двойственной задачи к задаче (1) — (3) (показана слева от соответствующего ограничения).
Двойственная задача имеет вид:
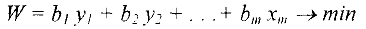
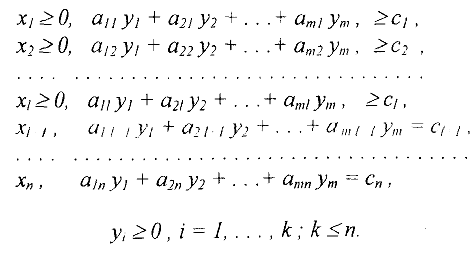
Задачи (1) — (3) и (4) — (6) образуют пару задач, называемую в линейном программировании двойственной парой.
Сравнивая две задачи, видим, что двойственная задача по отношению к исходной (прямой) содержит те же самые коэффициенты a,j, b„ Cj и составляется согласно следующим правилам:
- Целевая функция (1) исходной задачи задается на максимум, а целевая функция (4) двойственной задачи — на минимум.
- Матрица
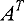 , составленная из коэффициентов при неизвестных в системе ограничений (5) двойственной задачи получается из матрицы
, составленная из коэффициентов при неизвестных в системе ограничений (5) двойственной задачи получается из матрицы 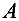 прямой задачи транспонированием (т.е. заменой строк столбцами):
прямой задачи транспонированием (т.е. заменой строк столбцами):
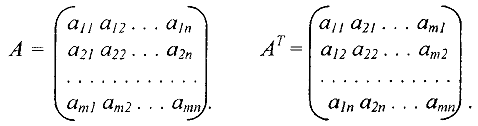
- Число переменных в двойственной задаче (4)-(6) равно числу ограничений в системе (2) прямой задачи, а число ограничений в системе (5) двойственной задачи равно числу переменных в прямой задаче.
- Коэффициентами при неизвестных в целевой функции (4) двойственной задачи являются свободные члены в системе (2) прямой задачи и наоборот.
- Если переменная
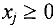 , то
, то  -е ограничение в системе (5) двойственной задачи является неравенством »
-е ограничение в системе (5) двойственной задачи является неравенством » 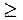 «. Если же переменная
«. Если же переменная 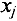 может иметь любой знак, то
может иметь любой знак, то 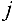 -е ограничение в системе (5) представляет собой уравнение.
-е ограничение в системе (5) представляет собой уравнение.
Каждая из задач двойственной пары (1) — (3) и (4) — (6) фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач, тем самым находится решение и другой задачи. Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже теоремами двойственности.
Теорема 1. (Основная теорема двойственности). Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план причем значения целевых функций задач при их оптимальных планах совпадают, т.е. 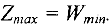
Если же целевая функция одной из задач не ограничена (для исходной (1) — (3) — сверху, для двойственной (4) — (6) — снизу), то другая задача вообще не имеет допустимых решений.
Теорема 2. (Вторая теорема двойственности). Для того, что бы два допустимых решения
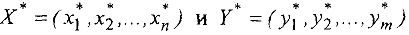
пары двойственных задач были их оптимальными решениями, необходимо и достаточно, чтобы они удовлетворяли системам уравнений:
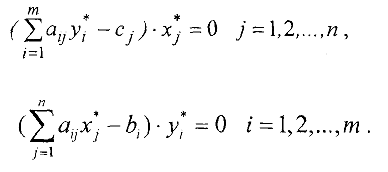
Замечание. Соотношения (7) верны только для ограничений в виде неравенств и для неотрицательных переменных.
Двойственный симплекс-метод, как и симплекс-метод, используется при нахождении решения задачи линейного программирования, записанной в канонической форме. Вместе с тем двойственный симплекс-метод можно применять при решении задачи ЛП, свободные члены системы ограничений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными).
Опишем алгоритм двойственного симплекс-метода. Рассмотрим задачу линейного программирования в канонической форме.
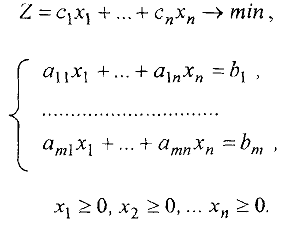
Пусть матрица ограничений  содержит единичную подматрицу порядка
содержит единичную подматрицу порядка 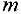 и первые
и первые 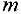 переменных
переменных 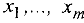 являются базисными. Среди чисел
являются базисными. Среди чисел 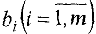 есть отрицательные. Вектор
есть отрицательные. Вектор 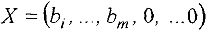 есть решение системы (9). Однако, это решение не является планом задачи (8) — (10), поскольку среди его компонент есть отрицательные числе (т.е. не выполняются ограничения (10)). Исключим базисные переменные из целевой функции
есть решение системы (9). Однако, это решение не является планом задачи (8) — (10), поскольку среди его компонент есть отрицательные числе (т.е. не выполняются ограничения (10)). Исключим базисные переменные из целевой функции 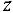 :
:
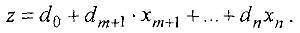
Предположим, что
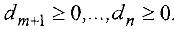
Шаг 1. Составить исходную симплексную таблицу.

IIIаг 2. Выяснить, имеется ли хотя бы одно отрицательное число среди элементов столбца 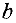 . Если нет, то перейти к шагу 8. Иначе — к шагу 3.
. Если нет, то перейти к шагу 8. Иначе — к шагу 3.
Шаг 3. Если отрицательных чисел в столбце 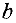 несколько, то выбрать наименьшее. Пусть, для определенности, это число
несколько, то выбрать наименьшее. Пусть, для определенности, это число
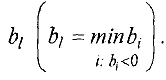
Строка с номером 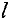 — ведущая.
— ведущая.
Шаг 4. Среди элементов 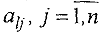 ведущей строки
ведущей строки 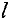 находят отрицательные. Если таковых нет, то исходная задача не имеет решения. В противном случае перейти к шагу 5.
находят отрицательные. Если таковых нет, то исходная задача не имеет решения. В противном случае перейти к шагу 5.
Шаг 5. Вычислить
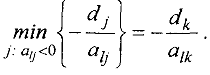
Столбец с номером 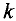 — ведущий,
— ведущий, 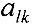 — ведущий элемент.
— ведущий элемент.
Шаг 6. С помощью ведущего элемента 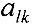 провести одну итерацию метода Жордана-Гаусса.
провести одну итерацию метода Жордана-Гаусса.
Шаг 7. Построить новую симплексную таблицу и перейти к шагу 2.
Шаг 8. Задача линейного программирования (8) — (10) решена. По последней симплексной таблице выписать оптимальный план и минимальное значение целевой функции задачи (8) — (10).
Замечание. Если среди чисел 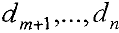 есть отрицательные,
есть отрицательные,
то следует в системе ограничений (9) преобразовать свободные члены 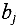 в неотрицательные, умножив на (-1) строки, содержащие отрицательные свободные члены и решать задачу (8) — (10) методом искусственного базиса.
в неотрицательные, умножив на (-1) строки, содержащие отрицательные свободные члены и решать задачу (8) — (10) методом искусственного базиса.
Пример оформления заказа №2.
Решить задачу математического программирования:
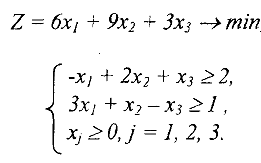
Решение:
Составим для задачи (11) двойственную:
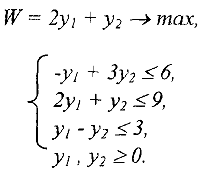
Для решения задачи (11) двойственным симплекс-методом приведем ее к каноническому виду. Для этого умножим первое и второе ограничения на (-1) и добавим соответственно неотрицательные дополнительные переменные 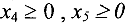 :
:
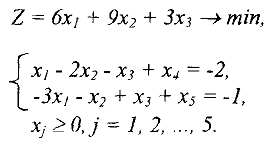
Базисными переменными здесь являются переменные 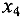 и
и 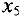 . Поскольку все коэффициенты
. Поскольку все коэффициенты 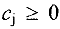 , то критерий оптимальности для этого базисного решения выполнен, однако само решение
, то критерий оптимальности для этого базисного решения выполнен, однако само решение  = (0, 0, 0, -2, -1) содержит отрицательные переменные, то есть не является допустимым. Естественно попытаться вывести отрицательные (не являющиеся допустимыми) переменные из базиса, сохранив при этом неотрицательность коэффициентов целевой функции, так как в этом случае полученное допустимое решение будет являться и оптимальным. Такой подход является содержанием двойственного симплекс-метода. Проиллюстрируем его на примере решения задачи (13).
= (0, 0, 0, -2, -1) содержит отрицательные переменные, то есть не является допустимым. Естественно попытаться вывести отрицательные (не являющиеся допустимыми) переменные из базиса, сохранив при этом неотрицательность коэффициентов целевой функции, так как в этом случае полученное допустимое решение будет являться и оптимальным. Такой подход является содержанием двойственного симплекс-метода. Проиллюстрируем его на примере решения задачи (13).
Составим исходную симплекс-таблицу.
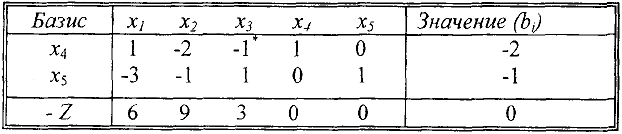
Вычисляем
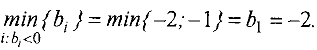
Из базиса будем выводить переменную 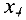 . Следовательно, первая строка таблицы является разрешающей. Среди элементов разрешающей строки находим отрицательные
. Следовательно, первая строка таблицы является разрешающей. Среди элементов разрешающей строки находим отрицательные
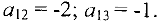
Определяем
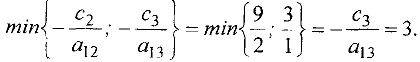
Столбец, в котором достигается этот минимум, соответствует переменной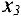 .
.
Этот столбец является разрешающим и разрешающим элементом является элемент 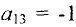 . Это делается для того, чтобы элементы последней строки остались неотрицательными. Проводим одну итерацию метода Жордана-Гаусса относительно этого элемента, т.е. из базиса исключаем переменную
. Это делается для того, чтобы элементы последней строки остались неотрицательными. Проводим одну итерацию метода Жордана-Гаусса относительно этого элемента, т.е. из базиса исключаем переменную 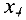 и включаем в базис переменную
и включаем в базис переменную 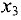 . Новая симплекс-таблица имеет вид:
. Новая симплекс-таблица имеет вид:
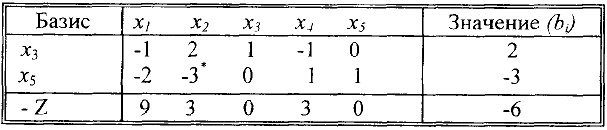
Элемент 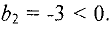 Следовательно, разрешающей является вторая строка таблицы. Как и ранее, находим
Следовательно, разрешающей является вторая строка таблицы. Как и ранее, находим
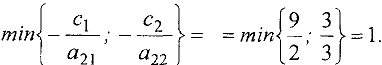
Следовательно второй столбец — разрешающий, переменную 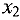 включаем в базис, переменную
включаем в базис, переменную 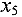 исключаем из базиса. Пересчитывая таблицу относительно элемента
исключаем из базиса. Пересчитывая таблицу относительно элемента 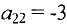 , получаем новую таблицу:
, получаем новую таблицу:

Среди элементов столбца ‘Значение» нет отрицательных чисел. В 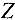 -строке также нет отрицательных чисел. Следовательно, найден оптимальный план:
-строке также нет отрицательных чисел. Следовательно, найден оптимальный план: 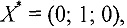 , при этом
, при этом 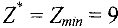 . По последней симплекс-таблице находим решение двойственной задачи (12). Для этого выясняем, какие переменные задачи (11) входили в исходный базис. В первоначальной таблице это —
. По последней симплекс-таблице находим решение двойственной задачи (12). Для этого выясняем, какие переменные задачи (11) входили в исходный базис. В первоначальной таблице это — 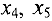 . В последней симплекс-таблице находим элементы
. В последней симплекс-таблице находим элементы 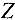 — строки, соответствующие этим базисным переменным
— строки, соответствующие этим базисным переменным 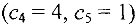 и прибавляем к ним соответствующие коэффициенты исходной целевой функции
и прибавляем к ним соответствующие коэффициенты исходной целевой функции 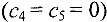 . В результате получаем
. В результате получаем
Транспортная задача
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из 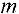 пунктов отправления
пунктов отправления 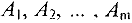 в
в 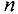 пунктов назначения
пунктов назначения 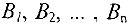 . При этом в качестве критерия оптимальности берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.
. При этом в качестве критерия оптимальности берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.
Математическая модель транспортной задачи имеет вид:
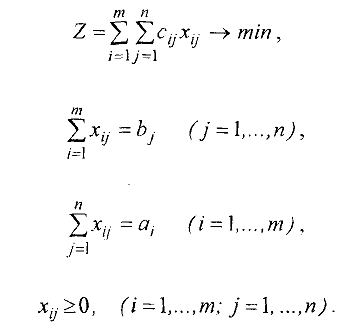
Здесь 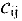 — тарифы перевозки единицы груза из
— тарифы перевозки единицы груза из 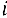 -гo пункта отправления
-гo пункта отправления 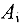 в
в 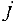 -й пункт назначения
-й пункт назначения 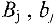 — потребность в грузе в
— потребность в грузе в 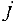 -м пункте назначения,
-м пункте назначения, 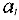 -запасы груза в
-запасы груза в 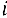 -м пункте отправления.
-м пункте отправления.
Наличие линейных уравнений (15) и (16) обеспечивает доставку необходимого количества груза в каждый из пунктов назначения и вывоз всего имеющегося груза из всех пунктов отправления. При этом, ввиду (17), исключаются обратные перевозки. Задача (14) — (17) является частным случаем задачи линейного программирования, однако, в силу своей специфики решается специальным методом. Если выполняется гак называемое условие баланса то такая транспортная задача называется закрытой. Если условие баланса (18) не выполняется, то задача называется открытой.
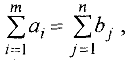
Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие баланса (18).
Если
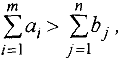
то вводится фиктивный 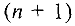 — й пункт назначения с потребностью
— й пункт назначения с потребностью
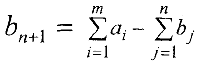
и соответствующие тарифы полагают равными нулю, т.е.
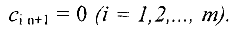
Аналогично, при
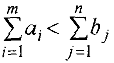
вводится фиктивный, 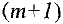 — й пункт отправления с запасами груза
— й пункт отправления с запасами груза
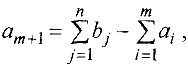
при этом тарифы на перевозку из этого пункта также полагают равными нулю,
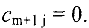
Для решения задачи (14) — (17) применяется метод потенциалов, который по существу, является другой формой симплекс-метода.
Опишем алгоритм метода. Исходные данные транспортной задачи запишем в таблице
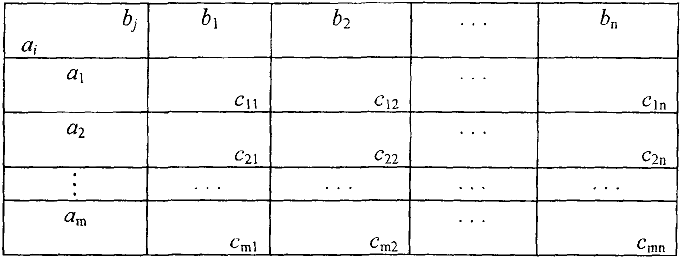
Построение начального опорного плана. Система ограничений (15)-(16) содержит 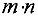 неизвестных и
неизвестных и 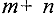 уравнений, связанных отношением (18). Невырожденный опорный план задачи содержит
уравнений, связанных отношением (18). Невырожденный опорный план задачи содержит 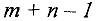 положительных перевозок или компонент. Таким образом, если каким-либо способом получен невырожденный опорный план задачи, то в матрице
положительных перевозок или компонент. Таким образом, если каким-либо способом получен невырожденный опорный план задачи, то в матрице 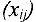 значений его компонент положительными являются только
значений его компонент положительными являются только 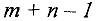 , а остальные равны нулю.
, а остальные равны нулю.
Клетки, в которых находятся отличные от нуля перевозки, называются занятыми, остальные — незанятыми. Занятые клетки соответствуют базисным неизвестным, и для невырожденного опорного плана их количество равно 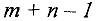 .
.
Для построения начального опорного плана применим метод минимальной стоимости.
Выбираем клетку с минимальной стоимостью (если их несколько, возьмем любую из них). Пусть, например,
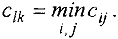
Тогда в клетку 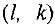 записывают число
записывают число
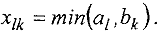
При этом, если
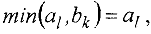
то значение 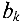 уменьшают на
уменьшают на 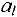 и «закрывают» строку с номером
и «закрывают» строку с номером 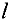 , так как ресурсы
, так как ресурсы 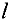 -го поставщика исчерпаны. Если
-го поставщика исчерпаны. Если
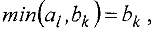
то значение 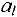 уменьшают на
уменьшают на 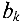 и «закрывают» столбец с номером
и «закрывают» столбец с номером 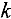 , что означает удовлетворение спроса
, что означает удовлетворение спроса 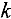 -го потребителя. Если же
-го потребителя. Если же 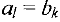 , то «закрывают» строку или столбец по выбору.
, то «закрывают» строку или столбец по выбору.
Вышеописанную процедуру повторяют для оставшейся транспортной таблицы до тех пор, пока не будут закрыты все строки и столбцы.
Построение системы потенциалов. Система потенциалов строится для невырожденного опорного плана и имеет вид:
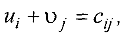
где 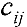 — стоимость перевозки единицы груза занятой (базисной) клетки в
— стоимость перевозки единицы груза занятой (базисной) клетки в 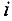 — й строке и
— й строке и 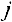 — м столбце.
— м столбце.
Вычисление потенциалов удобно проводить по таблице, положив равным нулю один из потенциалов и затем последовательно находя все остальные потенциалы вычитанием из стоимостей базисных клеток уже известных потенциалов. Потенциалы поставщиков 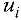 записывают справа, а потенциалы потребителей
записывают справа, а потенциалы потребителей 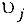 — внизу транспортной таблицы.
— внизу транспортной таблицы.
- Проверка опорного плана на оптимальность. Для каждой свободной клетки вычисляют оценки
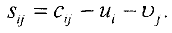
Если 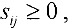 то опорный план оптимален и задача решена. В противном случае план не является оптимальным, следовательно, его нужно улучшить.
то опорный план оптимален и задача решена. В противном случае план не является оптимальным, следовательно, его нужно улучшить.
- Построение цикла и нахождение нового опорного плана. Среди отрицательных оценок выбираем наименьшую. Пусть
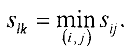
В клетке 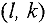 нарушено условие оптимальности. Для улучшения опорного плана необходимо в клетку
нарушено условие оптимальности. Для улучшения опорного плана необходимо в клетку 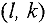 отправить некоторое количество груза, превратив ее тем самым в базисную. Эта операция эквивалентна действию по замене базиса в симплекс-методе.
отправить некоторое количество груза, превратив ее тем самым в базисную. Эта операция эквивалентна действию по замене базиса в симплекс-методе.
Клетку 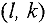 отмечают знаком «+» и затем строят цикл, расставляя поочередно знаки «-» и «+» в базисных клетках так, чтобы в строках и столбцах стояло по одному знаку «+» иди «-». Цикл строится единственным образом.
отмечают знаком «+» и затем строят цикл, расставляя поочередно знаки «-» и «+» в базисных клетках так, чтобы в строках и столбцах стояло по одному знаку «+» иди «-». Цикл строится единственным образом.
Обозначим 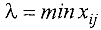 , где
, где 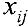 — перевозки, стоящие в вершинах цикла, отмеченных знаком «-». Величина
— перевозки, стоящие в вершинах цикла, отмеченных знаком «-». Величина 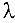 определяет количество груза, которое можно перераспределить по найденному циклу. Значение
определяет количество груза, которое можно перераспределить по найденному циклу. Значение 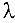 записывают в незанятую клетку
записывают в незанятую клетку 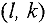 . Двигаясь по циклу, вычитают или прибавляют
. Двигаясь по циклу, вычитают или прибавляют 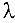 к объемам перевозок, расположенных в клетках, помеченными знаками «-» или «+» соответственно. Перевозки в остальных базисных клетках остаются без изменения. Переходим к построению системы по тенциалов.
к объемам перевозок, расположенных в клетках, помеченными знаками «-» или «+» соответственно. Перевозки в остальных базисных клетках остаются без изменения. Переходим к построению системы по тенциалов.
Замечание. Если условие баланса нарушено, т.е.
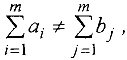
то вводят фиктивного поставщика
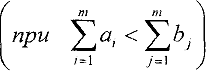
или потребителя
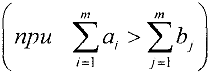
с потребностью
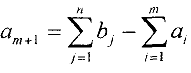
или поставкой
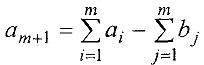
соответственно. Стоимости соответствующих перевозок полагаются равными нулю. При построении начального опорного плана в этом случае фиктивные клетки заполняются в последнюю очередь.
Пример. Компания контролирует 3 фабрики, производительность которых в неделю (в тыс. изделий) задается вектором
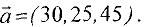
Компания заключила договоры с четырьмя заказчиками, еженедельные потребности которых (в тыс.изделий) задаются вектором
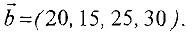
Стоимость транспортировки 1 тыс. изделий с 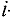 -й фабрики
-й фабрики 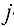 -му заказчику задается матрицей тарифов
-му заказчику задается матрицей тарифов
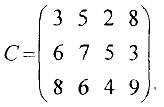
Требуется определить оптимальный план перевозок с целью минимизации суммарных затрат на транспортировку.
Так как
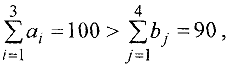
то введем в рассмотрение фиктивного 5-го заказчика с потребностью в
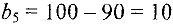
(тыс. ед.) груза. При этом положим
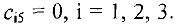
Исходные данные запишем в виде таблицы.
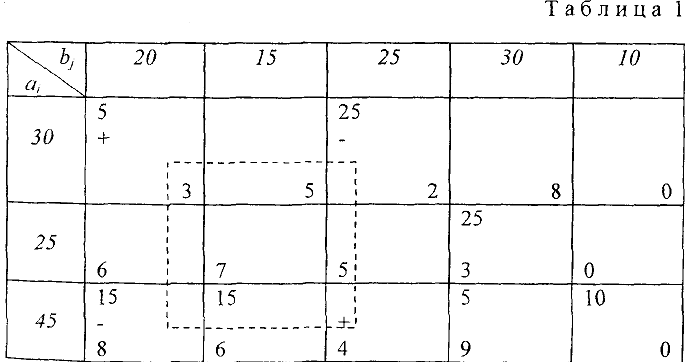
Построим начальный опорный план методом минимального элемента. Первой заполним клетку (1, 3) т. к. тариф этой клетки 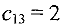 меньше других тарифов (фиктивный столбец заполняется в последнюю очередь). Поставка для «легки (1,3) будет равна
меньше других тарифов (фиктивный столбец заполняется в последнюю очередь). Поставка для «легки (1,3) будет равна 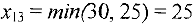 . Записываем это число в верхний левый угол клетки. Это означает, что с первой фабрики третьему заказчику апанируется поставить 25 тыс. ед. груза. При этом требования 3-го заказчика будут полностью удовлетворены и мы закрываем 3-й столбец. Затем в оставшейся части таблицы (без 3-го столбца) ищем клетку с минимальным тарифом. Таких клеток две (1, 1) и (2, 4). Заполняем любую из них, например, клетку (1, 1). Остаток продукции 1-й фабрики равен 30 -25 = 5. Поэтому записать в клетку (1,1) можно
. Записываем это число в верхний левый угол клетки. Это означает, что с первой фабрики третьему заказчику апанируется поставить 25 тыс. ед. груза. При этом требования 3-го заказчика будут полностью удовлетворены и мы закрываем 3-й столбец. Затем в оставшейся части таблицы (без 3-го столбца) ищем клетку с минимальным тарифом. Таких клеток две (1, 1) и (2, 4). Заполняем любую из них, например, клетку (1, 1). Остаток продукции 1-й фабрики равен 30 -25 = 5. Поэтому записать в клетку (1,1) можно
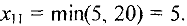
Поскольку с первой фабрики вывезен весь груз (30 тыс. ед.), то закрываем первую строку. Далее поступаем аналогично, заполняя свободные клетки в порядке возрастания тарифов, закрывая каждый раз нужные строку или столбец. В результате начальный план имеет вид (см. табл.1):
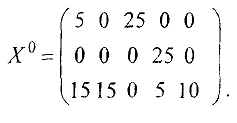
Проверим этот план на оптимальность. Для этого найдем потенциалы 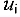 и
и 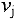 поставщиков и потребителей. Для этого по запятым клеткам составим систему уравнений вида
поставщиков и потребителей. Для этого по запятым клеткам составим систему уравнений вида 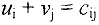 :
:
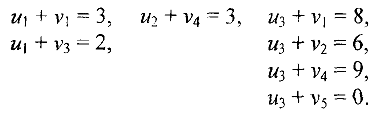
Поскольку уравнений в системе столько же, сколько занятых клеток, то есть 7, а неизвестных — 8, то система имеет бесконечное множество решений. Положим, например, 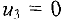 . Тогда остальные потенциалы находятся однозначно:
. Тогда остальные потенциалы находятся однозначно:
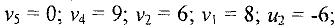
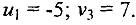
Теперь вычисляем оценки 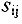 свободных клеток по формуле
свободных клеток по формуле
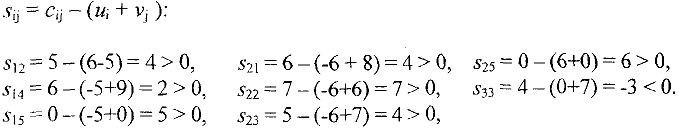
Среди оценок есть отрицательная  , следовательно план не является оптимальным. Необходимо улучшить план, загружая клетку с отрицательной оценкой.
, следовательно план не является оптимальным. Необходимо улучшить план, загружая клетку с отрицательной оценкой.
Для этого построим для клетки (3, 3) цикл с вершинами в загруженных клетках (см. табл. 1), расставляя поочередно в вершинах, начиная с клетки (3, 3), знаки «+» и « — ». Из поставок в клетках, помеченных знаком «минус», выбираем наименьшую:
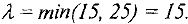
Для получения нового опорного плана изменим поставки в вершинах цикла: к поставкам в клетках, помеченных знаком «+», прибавляем величину 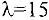 , в клетках, помеченных знаком «-», вычитаем эту величину 15. Новый опорный план поместим в табл. 2.
, в клетках, помеченных знаком «-», вычитаем эту величину 15. Новый опорный план поместим в табл. 2.
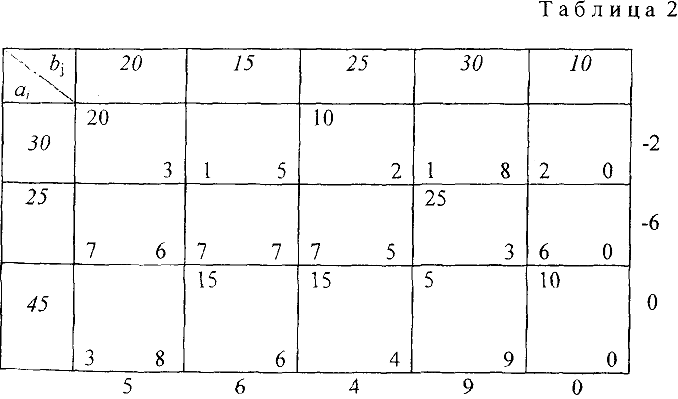
Исследование этого плана на оптимальность аналогично предыдущему. Вычисленные значения потенциалов записаны справа и снизу таблицы, а оценки 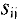 свободных клеток поместим в левых нижних углах этих клеток. Поскольку среди оценок нет отрицательных, то найденный план является оптимальным. Выписываем матрицу
свободных клеток поместим в левых нижних углах этих клеток. Поскольку среди оценок нет отрицательных, то найденный план является оптимальным. Выписываем матрицу 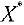 (без последнего столбца):
(без последнего столбца):
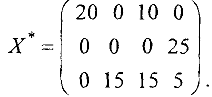
Минимальные суммарные затраты по оптимальному плану составляют:
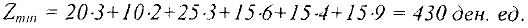
Из таблицы 2 видно, что избыточная продукция в количестве 10 тыс. изд. остается на третьей фабрике.
Задача о максимальном потоке в сети
Рассмотрим сеть 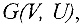 , где
, где 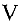 множество вершин, a
множество вершин, a 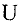 множество дуг их соединяющих, дуге
множество дуг их соединяющих, дуге 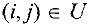 поставлено в соответствие неотрицательное число
поставлено в соответствие неотрицательное число 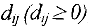 , называемое пропускной способностью этой дуги (если дуга
, называемое пропускной способностью этой дуги (если дуга 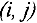 — неориентированная, то полагаем
— неориентированная, то полагаем 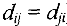 . Выделим в сети две вершины. Одну из них назовем источником и обозначим
. Выделим в сети две вершины. Одну из них назовем источником и обозначим 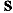 , а другую — стоком и обозначим
, а другую — стоком и обозначим 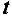 .
.
Каждой дуге 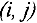 сети поставим в соответствие неотрицательное число
сети поставим в соответствие неотрицательное число 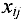 , которое назовем потоком на дуге
, которое назовем потоком на дуге 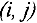 . Потоком из источника
. Потоком из источника  в сток
в сток 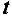 в сети
в сети 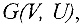 называется множество неотрицательных чисел
называется множество неотрицательных чисел 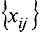 удовлетворяющих ограничениям:
удовлетворяющих ограничениям:
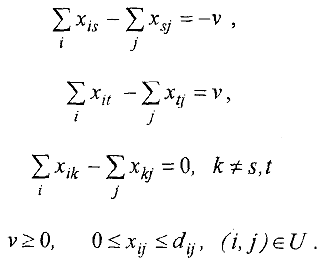
Неотрицательная величина v называется величиной потока в сети. Ограничения (19), (20) означают, что суммарная величина 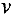 потока, выходящего из источника
потока, выходящего из источника 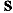 , равна суммарной величине
, равна суммарной величине 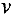 потока, входящего в сток
потока, входящего в сток 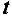 . Ограничения (21) выражают тот факт, что в каждую вершину (кроме источника и стока) приходит столько потока, сколько из нее уходит. Если для дуги
. Ограничения (21) выражают тот факт, что в каждую вершину (кроме источника и стока) приходит столько потока, сколько из нее уходит. Если для дуги 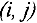 имеем
имеем 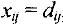 , то дуга
, то дуга 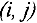 называется насыщенной потоком.
называется насыщенной потоком.
Итак, задача нахождения максимального потока является задачей линейного программирования с целевой функцией
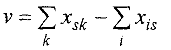
и ограничениями (19) — (22). В силу своей специфики для ее решения существует более эффективный алгоритм, чем симплекс-метод.
Разобьем множество вершин 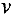 сети
сети 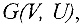 на два непересекающихся подмножества
на два непересекающихся подмножества 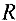 и
и 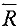
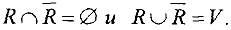
Разрезом 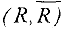 сети
сети 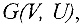 называется множество всех дуг
называется множество всех дуг 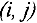 , таких, что-либо
, таких, что-либо
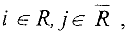
либо
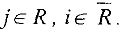
Т.е. разрез — это множество всех дуг, концевые вершины которых принадлежат разным множествам:
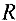 и
и 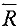 . При этом положим
. При этом положим
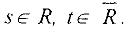
Тогда мы получим разрез, отделяющий источник  от стока
от стока  . Если удалить все дуги некоторого разреза, отделяющего источник
. Если удалить все дуги некоторого разреза, отделяющего источник  от стока
от стока 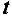 , то на сети не останется пути ведущего из
, то на сети не останется пути ведущего из 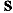 в
в 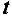 .
.
Пропускной способностью разреза 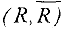 называется величина
называется величина
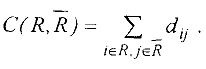
Разрез, отделяющий источник от стока и обладающий минимальной пропускной способностью, называется минимальным разрезом.
Теорема (о максимальном потоке и минимальном разрезе). В любой сети величина максимального потока из источника  в сток
в сток  равна пропускной способности минимального разреза.
равна пропускной способности минимального разреза.
Пусть на сети имеется некоторый поток, который не является максимальным. Покажем, как найти путь, увеличивающий этот поток.
Алгоритм расстановки пометок нахождения увеличивающего пути
IIIаг 1. Источник  получает метку
получает метку 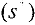 .
.
Шаг 2. Для всех дуг 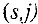 выходящих из вершины s, соответствующие вершины
выходящих из вершины s, соответствующие вершины 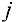 получают метку
получают метку 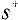 если
если 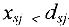 . Для дуг
. Для дуг 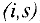 , входящих в вершину
, входящих в вершину 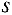 , соответствующие вершины
, соответствующие вершины 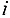 получают метку
получают метку 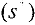 , если
, если 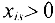 .
.
Шаг 3. Просматриваем все вершины, помеченные на 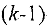 — м шаге. Для каждой такой вершины
— м шаге. Для каждой такой вершины 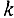 , соответствующие им вершины
, соответствующие им вершины 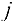 , для которых
, для которых 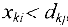 , получают метку
, получают метку 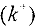 , для всех дуг
, для всех дуг 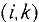 , входящих в вершину
, входящих в вершину 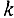 , соответствующих им вершины
, соответствующих им вершины 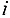 , для которых
, для которых 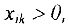 , получают метку
, получают метку 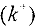 .
.
Алгоритм заканчивает работу одним из двух состояний: а) после некоторого шага мы не можем пометить ни одной вершины, и сток 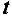 остался непомеченным. Это означает, что имеющийся поток является максимальным, а
остался непомеченным. Это означает, что имеющийся поток является максимальным, а 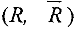 , где
, где 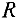 -множество помеченных,
-множество помеченных, 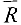 — множество непомеченных вершин, образует минимальный разрез; б) сток l оказался помеченным. Двигаясь от стока
— множество непомеченных вершин, образует минимальный разрез; б) сток l оказался помеченным. Двигаясь от стока 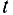 к вершине, номер которой указан в ее метке и т.д., мы придем к источнику.
к вершине, номер которой указан в ее метке и т.д., мы придем к источнику.
Алгоритм Форда — построения максимального потока в сети
Начальный. Выбираем некоторый поток 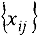 в сети
в сети 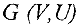 (например
(например 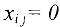 для всех дуг
для всех дуг 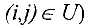 .
.
Общая итерация 1. Применяем алгоритм нахождения увеличивающего пути из источника 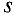 в сток
в сток 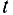 . Если такого пути нет, то построенный поток является максимальным. Алгоритм заканчивает работу. Если увеличивающий путь найден, то переходим к 2.
. Если такого пути нет, то построенный поток является максимальным. Алгоритм заканчивает работу. Если увеличивающий путь найден, то переходим к 2.
- В найденном увеличивающем пути обозначим через
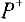 множество прямых, а
множество прямых, а 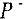 — множество обратных дуг пути и вычисляем величину
— множество обратных дуг пути и вычисляем величину
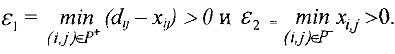
Полагаем
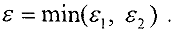
Увеличиваем поток вдоль пути 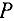 на величину
на величину 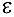 , полагая
, полагая
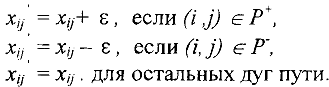
Переходим к 1.
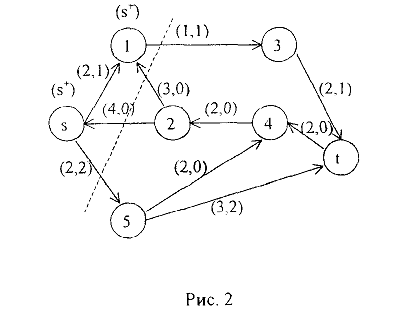
Рассмотрим пример. На рис.1, изображена сеть. Первое число в скобках указывает пропускную способность дуги, второе — дуговой поток.
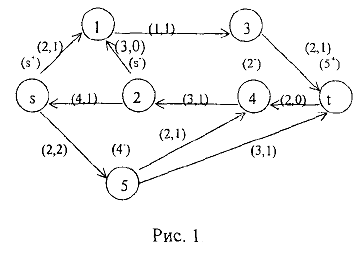
Найдем увеличивающий путь.
Общая итерация: Шаг 1. Источник  получает пометку
получает пометку 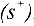 . Шаг 2. Так как
. Шаг 2. Так как
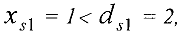
то вершина 1 получает метку 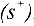 . Вершина 2 получает метку
. Вершина 2 получает метку 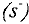 , т.к.
, т.к. 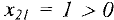 . Вершина 5 не может быть помечена, т.к.
. Вершина 5 не может быть помечена, т.к. 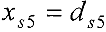 (дуга (
(дуга (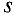 , 5) — насыщенная).
, 5) — насыщенная).
Шаг 3. Соседними вершинами с вновь помеченными являются вершины 3 и 4. Вершина 3 помечена не может быть, так как 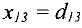 .Вершина 4 получает пометку (2), т.к.
.Вершина 4 получает пометку (2), т.к. 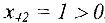 .
.
Шаг 4. Соседними с помеченной вершиной 4 являются вершины 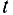 и 5. Вершина
и 5. Вершина 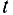 помечена не может быть, т.к.
помечена не может быть, т.к. 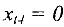 . Вершина 5 получает пометку (4′), т.к.
. Вершина 5 получает пометку (4′), т.к. 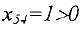 .
.
Шаг 5. Помечаем вершину 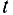 с меткой
с меткой 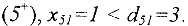 Увеличивающий путь:
Увеличивающий путь: 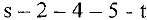 , причем на этом пути дуга
, причем на этом пути дуга 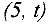 является прямой, а дуги
является прямой, а дуги 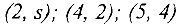 обратными. Увеличим поток вдоль этого пути по формулам (23). Находим
обратными. Увеличим поток вдоль этого пути по формулам (23). Находим
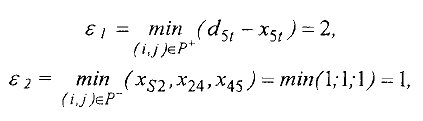
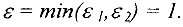
Полагаем
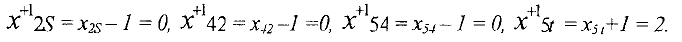
Величина суммарного потока в сети равна 3. Общая итерация 1. Для нового потока ищем увеличивающий путь методом расстановки пометок. Пометать удается только вершины  и 1. Следовательно, увеличивающего пути нет, и построенный поток является максимальным. Минимальный разрез
и 1. Следовательно, увеличивающего пути нет, и построенный поток является максимальным. Минимальный разрез 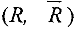 , где
, где
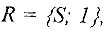
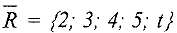
состоит из дуг
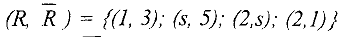
и обладает пропускной способностью
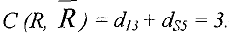
На рис. 2 минимальный разрез показан пунктирной линией.
Сетевое планирование
Основой методов сетевого планирования является сетевая модель (сетевой график), отражающая логическую взаимосвязь работ, входящий в некоторый комплекс, что позволяет осуществлять управление ходом выполнения этих работ.
Для построения сетевой модели необходимо, прежде всего, разбить весь комплекс на отдельные работы или операции и составить очередность выполнения этих работ. Для этого составляется список работ, которые непосредственно предшествуют каждой работе, а так же планируется время, необходимое для их выполнения.
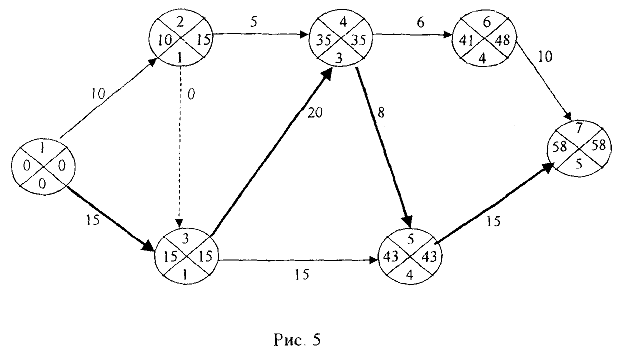
Полученные данные удобно заносить в таблицу. В табл. 1 приведены данные для проекта, состоящего из девяти работ.
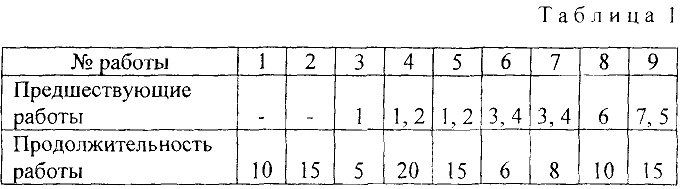
На основании данных, приведенных в таблице, строится график комплекса работ, входящих в проект. Каждая работа изображается в виде ориентированного отрезка (дуги). Связи между работами изображаются пунктирными линиями (дуги-связи). В результате получается сетевой график (начальная вершина дуги — начало, а конечная — завершение соответствующей работы):
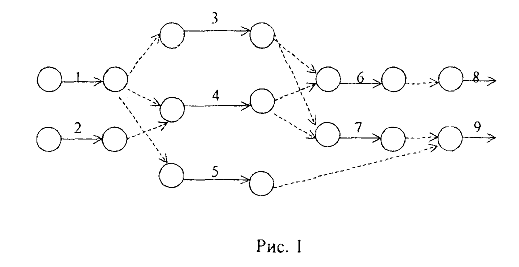
Предварительно следует упростить полученную сеть. Можно удалить некоторые дуги-связи, а начало и конец удаляемой дуги объединить в одну вершину. На рис. 2 изображена сеть, полученная после упрощения сети, изображенной на рис. 1.
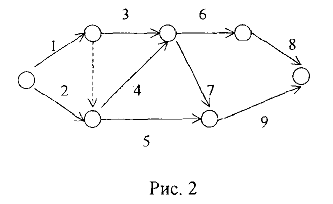
В сетевом графике каждая вершина является конечной для некоторых дуг(операций), входящих в нее или начальной для дуг (операций) из нее выходящих. Поэтому каждая вершина может трактоваться как событие, означающее завершение всех операций (дуг), для которых она является конечной и возможность начала выполнения всех операций (дух), для которых она является начальной. Начальной вершине соответствует событие, под которым подразумевается начало осуществления проекта, а конечной вершине соответствует событие — завершения выполнения всего комплекса работ.
После построения сетевого графика все его вершины нумеруются так, что нумерация является правильной.
Алгоритм правильной нумерации
Шаг 1. Нумеруем начальную вершину номером 1. Переходим к шагу 2.
Шаг 2. Удаляем из сети все выходящие из пронумерованных вершин дуги. Нумеруем в произвольном порядке вершины, в которые не входит ни одна дуга, произвольным образом возрастающими по порядку номерами. Шаг 2 проделываем до тех пор, пока не дойдем до конечной вершины, которой присваиваем следующий по порядку номер.
В результате правильной нумерации вершин сетевой график, приведенный на рис. 2 примет вид
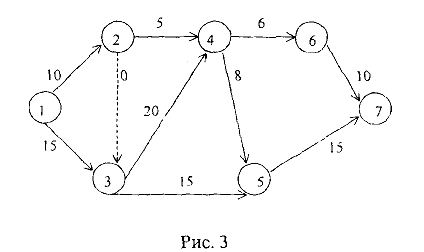
Номера работ на дугах соответственно заменены продолжительностью их выполнения (продолжительность фиктивной работы соответствующей дуги-связи полагаем равной 0).
Рассмотрим основные временные параметры сетевого графика. Пусть 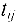 -продолжительность работы, для которой соответствующая дуга
-продолжительность работы, для которой соответствующая дуга 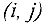 в сетевом графике имеет в качестве начальной — вершину с номером
в сетевом графике имеет в качестве начальной — вершину с номером 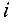 , а в качестве конечной — вершину с номером
, а в качестве конечной — вершину с номером 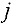 .
.
Ранним сроком начала работы 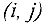 называется наименьшее допустимое время
называется наименьшее допустимое время 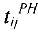 , когда может быть начато ее выполнение.
, когда может быть начато ее выполнение.
Если работа начата в ранний срок, то время ее окончания 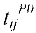 называется ранним сроком окончания
называется ранним сроком окончания
Ранний срок начала всех работ, для которых вершина 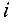 — начальная, называется ранним сроком наступления события
— начальная, называется ранним сроком наступления события 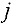 и обозначается
и обозначается 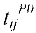 .
.
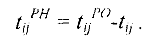
Ранний срок наступления конечного события называется критическим временем и обозначается 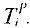 Таким образом, критическое время — это минимальный срок, за который может быть выполнен весь комплекс работ.
Таким образом, критическое время — это минимальный срок, за который может быть выполнен весь комплекс работ.
Каждый путь из начальной вершины в конечную, состоящий из дуг (работ) и дуг-связей продолжительностью 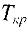 , называется критическим путем, а работы, составляющие такие пути — критическими работами.
, называется критическим путем, а работы, составляющие такие пути — критическими работами.
Поздними сроками начала и окончания работы 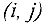 называется наибольшее допустимое время начала
называется наибольшее допустимое время начала 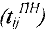 и окончания
и окончания 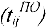 этой работы без нарушения сроков выполнения всего комплекса работ. Очевидно:
этой работы без нарушения сроков выполнения всего комплекса работ. Очевидно:
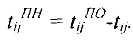
Наиболее поздний из поздних сроков окончания работ, входящих в вершину 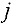 , называется поздним сроком наступления события
, называется поздним сроком наступления события 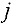 и обозначается
и обозначается 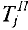 .
.
Рассмотрим работу 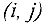 . Плановая продолжительность этой работы равна
. Плановая продолжительность этой работы равна 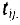 Максимально допустимое время, на которое можно увеличить продолжительность работы
Максимально допустимое время, на которое можно увеличить продолжительность работы 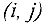 или задержать начало ее выполнения, при котором не изменится время выполнения всего проекта, называется полным резервом
или задержать начало ее выполнения, при котором не изменится время выполнения всего проекта, называется полным резервом 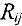 времени этой работы. Он равен:
времени этой работы. Он равен:
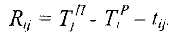
Резерв времени для работы 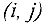 , использование которого не изменит ранние сроки наступления всех событий (т.е. все работы смогут начать выполняться в минимально возможные сроки), называется свободным и может быть вычислен по формуле
, использование которого не изменит ранние сроки наступления всех событий (т.е. все работы смогут начать выполняться в минимально возможные сроки), называется свободным и может быть вычислен по формуле
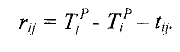
Очевидно, полный и свободный резерв времени любой работы, лежащей на критическом пути, равен нулю.
Алгоритм нахождения ранних сроков наступления событий
- Полагаем
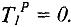
- Для
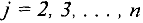 вычисляем
вычисляем
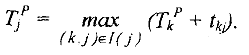
Здесь 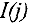 — множество всех дуг, входящих в вершину
— множество всех дуг, входящих в вершину 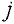 .
.
Критическое время 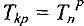 .
.
Алгоритм нахождения поздних сроков наступления событий
- Полагаем
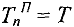 (как правило
(как правило 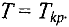 ).
). - Для
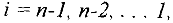 , вычисляем
, вычисляем
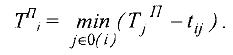
Здесь 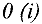 — множество вершин, которые являются конечным для дуг. выходящих из вершины
— множество вершин, которые являются конечным для дуг. выходящих из вершины 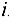 .
.
Рассмотрим сетевой график, описанный в табл. 1. События (вершины) сетевого графика изображены следующим образом:
В верхней четверти записан номер события (вершины) в соответствии с правильной нумерацией. Номер вершины 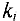 , при движении из которой получено значение
, при движении из которой получено значение 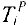 , заносится в нижнюю четверть. В левой четверти записывается ранний срок наступления события
, заносится в нижнюю четверть. В левой четверти записывается ранний срок наступления события 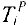 а в правой четверти — его поздний срок наступления
а в правой четверти — его поздний срок наступления 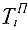 .
.
Найдем ранние сроки наступления каждого события для сетевого графика, изображенного на рис. 3.
Полагаем 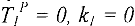 . Рассматриваем вершины в порядке возрастания их номеров.
. Рассматриваем вершины в порядке возрастания их номеров.
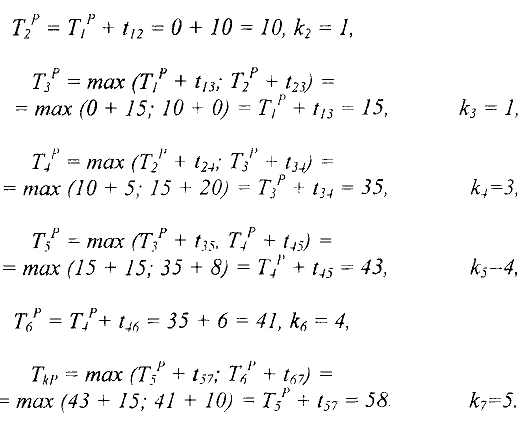
Построим критический путь, начиная с конечной вершины, двигаясь по номерам вершин 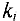 , стоящих в нижней четверти.
, стоящих в нижней четверти.
В результате получим 1 — 3 — 4 — 5 — 7. Найдем поздние сроки наступления событий. Полагаем время окончания всего проекта
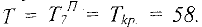
Поставим это значение в правую четверть конечной вершины 7.
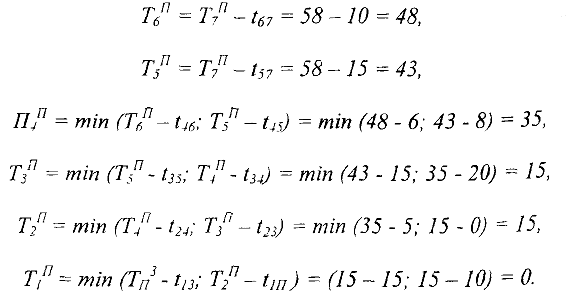
В результате получаем следующую сетевую модель, содержащую подробную информацию о ранних, поздних сроках наступления событий, критическом времени и критическом пути. Критический путь отмечен двойными линиями.
Задача о кратчайшем пути
Рассмотрим ориентированный граф 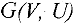 . Каждой дуге
. Каждой дуге 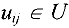 поставлено в соответствие неотрицательное число
поставлено в соответствие неотрицательное число 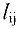 , которое мы будем называть длиной дуги
, которое мы будем называть длиной дуги 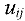 (если граф содержит неориентированную дугу, мы заменим ее парой противоположно ориентированных дуг, каждой из которых ставим в соответствие одно и то же число
(если граф содержит неориентированную дугу, мы заменим ее парой противоположно ориентированных дуг, каждой из которых ставим в соответствие одно и то же число 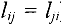 ). Рассмотрим некоторый ориентированный
). Рассмотрим некоторый ориентированный 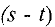 путь, соединяющий вершину
путь, соединяющий вершину 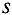 с вершиной
с вершиной 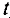 , и обозначим множество дуг входящих в него через
, и обозначим множество дуг входящих в него через 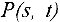 .
.
Длиной пути 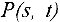 называется сумма
называется сумма
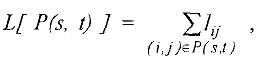
длин всех дуг, входящих в путь 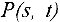 .
.
Теперь может быть сформулирована следующая задача : для выделенных вершин 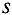 и
и 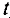 сети
сети 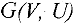 , среди всех путей их соединяющих, требуется найти путь
, среди всех путей их соединяющих, требуется найти путь
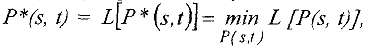
длина которого минимальна Если вершины сети трактовать как, например, города, а пути — как дороги между ними, протяженность которых известна, то задача состоит в нахождении кратчайшего маршрута между выделенными городами.
Прежде чем описать алгоритм нахождения кратчайших путей из выделенной вершины  сети
сети  во все остальные ее вершины, введем следующие обозначения. Для каждой вершины j сети
во все остальные ее вершины, введем следующие обозначения. Для каждой вершины j сети  будет обозначать длину кратчайшего
будет обозначать длину кратчайшего 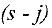 пути, a
пути, a 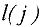 -длину некоторого (не обязательно кратчайшего) пути
-длину некоторого (не обязательно кратчайшего) пути 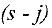 пути, а
пути, а 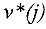 — номер предпоследней вершины кратчайшего пути, a
— номер предпоследней вершины кратчайшего пути, a 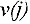 — номер предпоследней вершины рассматриваемого пути. В процессе работы алгоритма, на каждой его итерации очередной вершине у присваивается постоянная метка вида
— номер предпоследней вершины рассматриваемого пути. В процессе работы алгоритма, на каждой его итерации очередной вершине у присваивается постоянная метка вида 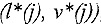 , где
, где 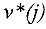 — номер предпоследней вершины в кратчайшем
— номер предпоследней вершины в кратчайшем 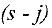 пути. Эта вершина присоединяется к множеству вершин
пути. Эта вершина присоединяется к множеству вершин  , имеющих постоянную метку.
, имеющих постоянную метку.
Обозначим через 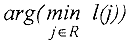 значение индекса
значение индекса  , при котором достигается минимальное значение величин
, при котором достигается минимальное значение величин  , то есть
, то есть
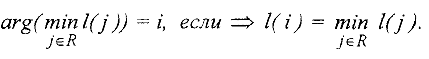
Алгоритм построения кратчайших путей в сети
Начальный шаг. Полагаем
если дуга
в противном случае. Для всех вершин v(j) — s.
Общая итерация. Шаг 1. Пусть 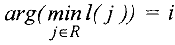 и вершина
и вершина 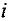 имеет метку
имеет метку 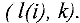 Если
Если 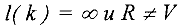 — алгоритм заканчивает работу.
— алгоритм заканчивает работу.
Если 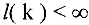 полагаем
полагаем
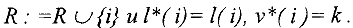
Если  — алгоритм заканчивает работу.
— алгоритм заканчивает работу.
Если  — переходим к шагу 2.
— переходим к шагу 2.
Шаг 2. Для всех  , таких, что
, таких, что 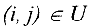 полагаем
полагаем
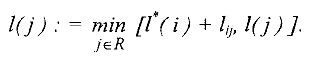
Если
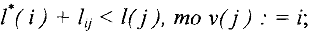
в противном случае 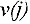 не меняется. Переходим к шагу 1 следующей итерации.
не меняется. Переходим к шагу 1 следующей итерации.
Рассмотрим итерацию, на которой алгоритм заканчивает работу. Это происходит на шаге 1, когда либо 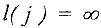 для всех
для всех 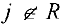 и
и 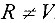 либо
либо 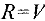 .
.
В первом случае ни одна дуга, начальной вершиной которой являются вершина множества  , не ведет в вершины, не принадлежащие этому множеству, а значит, не существует путей, ведущих из вершины s в вершины, не принадлежащие множеству
, не ведет в вершины, не принадлежащие этому множеству, а значит, не существует путей, ведущих из вершины s в вершины, не принадлежащие множеству  .
.
Во втором случае все вершины получили постоянную метку  , т.е. найдены кратчайшие расстояния от вершины
, т.е. найдены кратчайшие расстояния от вершины 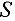 ко всем остальным вершинам сети.
ко всем остальным вершинам сети.
Заметим, что алгоритм явно не указывает кратчайший путь к вершине, а только его длину. Но воспользовавшись второй частью метки: 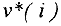 — его легко восстановить. Действительно,
— его легко восстановить. Действительно, 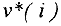 — номер предпоследней вершины в кратчайшем пути из
— номер предпоследней вершины в кратчайшем пути из 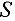 в
в 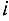 ; пусть
; пусть 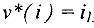 .
.
Но 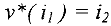 номер предпоследней вершины в кратчайшем пути из
номер предпоследней вершины в кратчайшем пути из 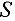 в
в 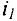 . Продолжая, мы найдем последовательность вершин
. Продолжая, мы найдем последовательность вершин  через которые проходит кратчайший путь.
через которые проходит кратчайший путь.
Рассмотрим работу алгоритма на следующем примере.
Найти кратчайшие пути из вершины S во все остальные вершины сети, изображенной на рис.1 (числа над дугами равны их длинам).
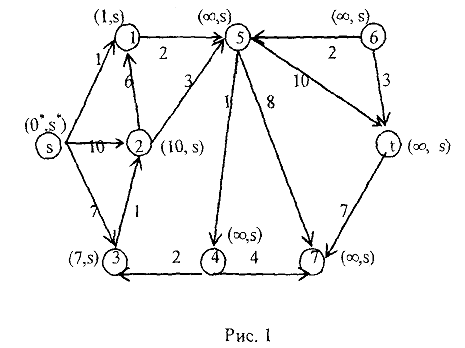
На начальном плане вершина  получает постоянную метку
получает постоянную метку  ,
, , соседние с ней вершины 1, 2, 3 получают временные метки
, соседние с ней вершины 1, 2, 3 получают временные метки  соответственно, а остальные вершины получают временные метки
соответственно, а остальные вершины получают временные метки  . (рис. 1).
. (рис. 1).
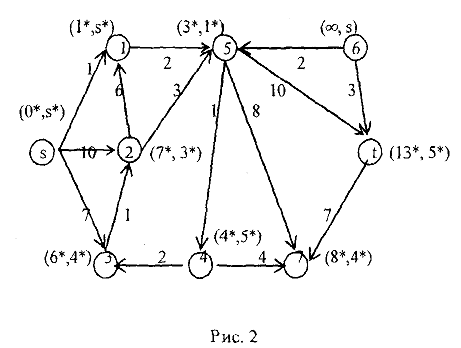
Итерация 1.
1) Минимальное значение первой части меток всех вершин равно 1 для первой вершины, т.е.
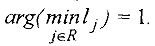
Метка первой вершины становится постоянной. Полагаем
переходим к шагу 2.
2) Просматриваем все вершины, соседние с вершиной, получившей постоянную метку (вершиной 1).
Для вершины 5 имеем
поэтому полагаем
Для вершины 2 имеем
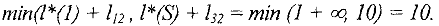
Так как
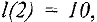
то метка вершины 2 не меняется. Переходим ко второй итерации и т.д.
Заметим, что на каждой итерации алгоритма одна очередная вершина  присоединяется к множеству
присоединяется к множеству  и получает постоянную метку
и получает постоянную метку 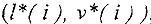 , которая в дальнейшем не меняется, а для остальных вершин
, которая в дальнейшем не меняется, а для остальных вершин 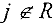 пересматриваются текущие значения величин
пересматриваются текущие значения величин 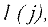 , некоторые из которых могут меняться и в дальнейшем. Результаты вычислений на начальном шаге (итерация 0) и на всех последующих итерациях удобно заносить в табл. 1. Если пара чисел
, некоторые из которых могут меняться и в дальнейшем. Результаты вычислений на начальном шаге (итерация 0) и на всех последующих итерациях удобно заносить в табл. 1. Если пара чисел 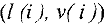 помечается символом ( * ), это означает, что вершина
помечается символом ( * ), это означает, что вершина 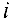 получила постоянную метку
получила постоянную метку 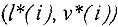 , которая в дальнейшем не меняется.
, которая в дальнейшем не меняется.
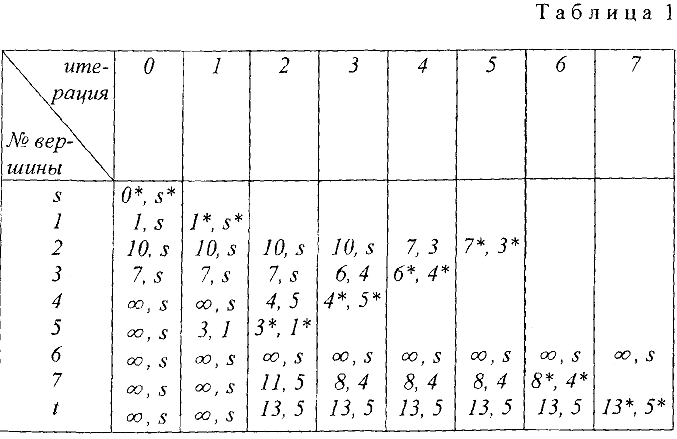
Алгоритм закончил работу на 7-й итерации случаем, когда
Это означает, что не существует пути, ведущего из вершины s в вершину 6. Для всех остальных вершин сети длины кратчайших путей найдены, а сами пути могут быть построены, как описано выше. Например, для вершины 2 имеем:
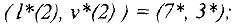
предыдущая вершина кратчайшего пути — 3. Для вершины 3

для вершины 4
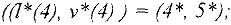
для вершины 5 —
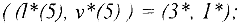
а для вершины 1 —
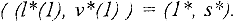
Таким образом, кратчайший (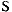 — 2) путь проходит через вершины —
— 2) путь проходит через вершины —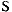 ,1, 5, 4, 3,2 и его длина равна 7.
,1, 5, 4, 3,2 и его длина равна 7.
Все дуги сети, входящие в кратчайшие пути, изображены на рис. 3. Пары чисел около вершин (рис. 2, 3) — это найденные в результате работы алгоритма постоянные метки вершин, первая часть которых 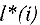 — длина кратчайшего
— длина кратчайшего 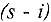 пути
пути 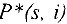 , а вторая — предпоследняя вершина этого пути (последней является вершина
, а вторая — предпоследняя вершина этого пути (последней является вершина  ).
).
Кратчайшие пути образуют дерево, но не остовное, так как вершина 6 не соединена ни с одной другой вершиной.
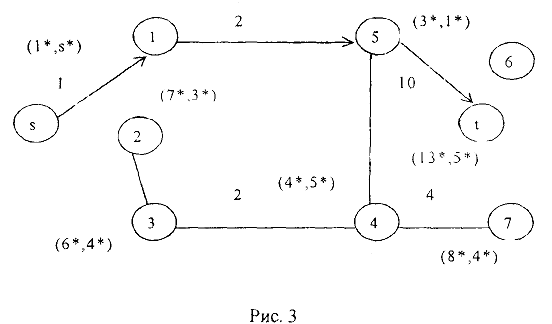
В заключение отметим, что поскольку на каждой итерации алгоритма только одна новая вершина и соответствующая дуга добавляются к множеству дуг и вершин, образующих кратчайшие пути, то отсюда следует, что множество кратчайших путей в любой сети образует дерево (т.е. не содержит цикла).
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированию
- Примеры решения задач по математическому программированию
- Заказать работу по математическому программированию
- Задачи математического программирования
- Задача линейного программирования
- Решение задач по линейному программированию
- Методы решения задач линейного программирования
- Графическое решение задач линейного программирования
- Графический метод решения задач линейного программирования
- Заказать работу по линейному программированию
- Помощь по линейному программированию
- Контрольная работа по линейному программированию
- Линейное программирование в Excel
- Курсовая работа по линейному программированию
