Оглавление:
Здравствуйте я подготовила краткое методическое пособие для студентов и школьников, оно содержит теорию и примеры решения, чтобы вы смогли подготовиться к экзаменам или другой любой работе.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Введение в математический анализ
Математический анализ – это обширная область математики с характерным объектом изучения (переменной величиной), своеобразным методом исследования (анализом посредством бесконечно малых или посредством предельных переходов), определенной системой основных понятий (функция, предел, производная, дифференциал, интеграл, ряд) и постоянно совершенствующимся и развивающимся аппаратом, основу которого составляют дифференциальное и интегральное исчисления.
Предел числовой последовательности. Предел функции
Число 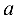 называется пределом числовой последовательности
называется пределом числовой последовательности 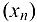 , если для любого числа
, если для любого числа 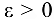 существует такой помер
существует такой помер 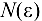 , что при всех
, что при всех 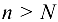 выполняется неравенство
выполняется неравенство 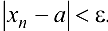 .
.
Обозначение предела функции 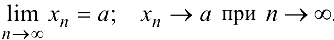
Число А называется пределом функции 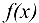 в точке
в точке 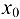 , если для любого числа
, если для любого числа 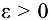 существует такое число
существует такое число 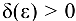 , что при всех
, что при всех 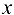 , удовлетворяющих условию
, удовлетворяющих условию 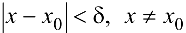 , выполняется неравенство
, выполняется неравенство 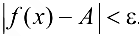
Обозначение предела функции 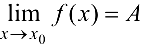 .
.
Если функции 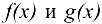 имеют конечные пределы при
имеют конечные пределы при 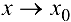 , то справедливы теоремы о пределах:
, то справедливы теоремы о пределах:
1. 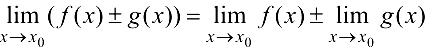
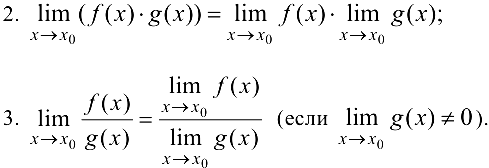
Возможно эта страница вам будет полезна:
| Предмет математический анализ |
Решение многих задач основано на следующих замечательных пределах:
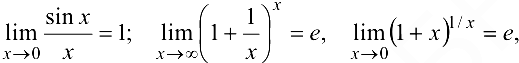
где 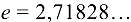
Примеры с решением:
Найти пределы:

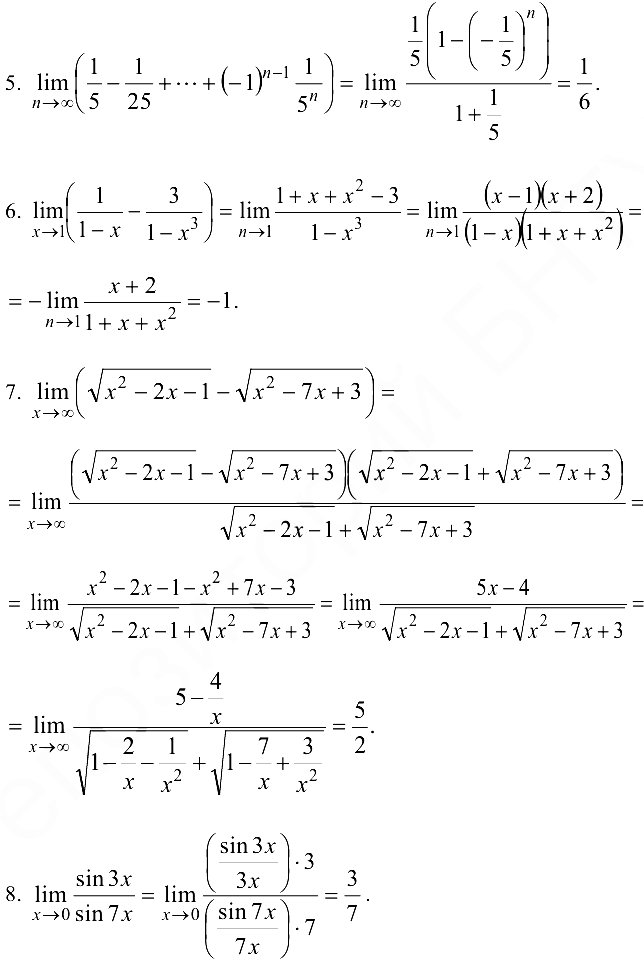
9. 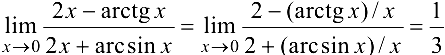 , так как
, так как
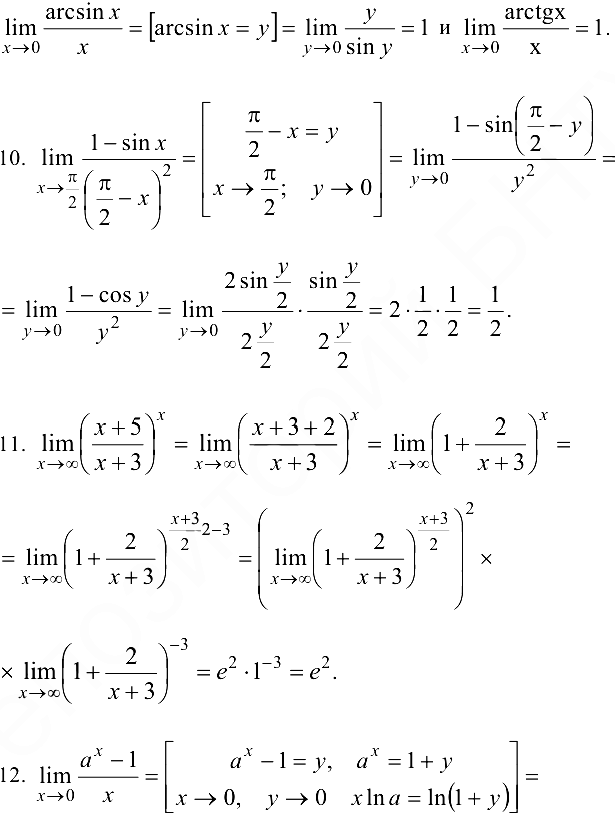
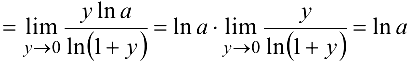 , так как
, так как
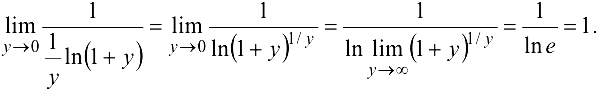
Бесконечно малые и бесконечно большие функции Сравнение бесконечно малых. Непрерывность функции. Точки разрыва и их классификация
Функция 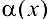 называется бесконечно малой при
называется бесконечно малой при 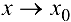 , если
, если 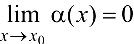 . Пусть
. Пусть 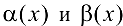 — бесконечно малые при
— бесконечно малые при  и существует предел их отношения
и существует предел их отношения 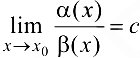 . Если
. Если 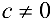 .,
., 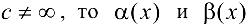 называются бесконечно малыми одного порядка малости. Обозначение
называются бесконечно малыми одного порядка малости. Обозначение 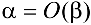 при
при 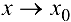 . Если с — 1, то
. Если с — 1, то 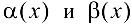 называются эквивалентными бесконечно малыми (обозначение:
называются эквивалентными бесконечно малыми (обозначение: 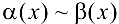 при
при  ). Если
). Если 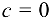 , то
, то 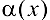 называется бесконечно малой высшего порядка, чем
называется бесконечно малой высшего порядка, чем 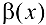 (обозначение
(обозначение 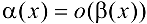 при
при  ).
).
При нахождении предела отношения двух бесконечно малых функций каждую из них можно заменить эквивалентной ей бесконечно малой, т.е. если 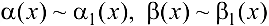 при
при  , то
, то
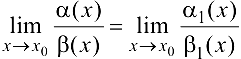
Пример 5.1.
Найти 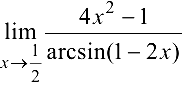
Решение:
При 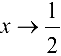 функции
функции 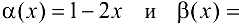
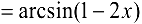 являются эквивалентными бесконечно малыми. Поэтому
являются эквивалентными бесконечно малыми. Поэтому
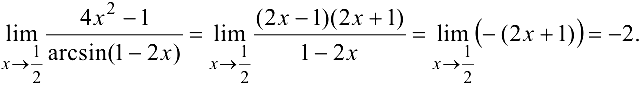
Функция 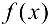 называется бесконечно большой при
называется бесконечно большой при  , если для любого положительного числа М существует такое число
, если для любого положительного числа М существует такое число 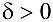 , что при всех
, что при всех 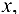 удовлетворяющих условию
удовлетворяющих условию 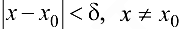 , выполняется неравенство
, выполняется неравенство 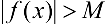 .
.
Обозначение
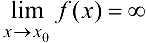
Функция 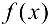 называется непрерывной в точке
называется непрерывной в точке 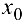 , если:
, если:
1) функция 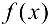 определена в точке
определена в точке 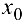 и ее окрестности;
и ее окрестности;
2) существует конечный предел функции 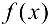 в точке
в точке 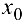 ;
;
3) этот предел равен значению функции в точке 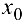 , т.е.
, т.е.
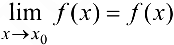
На практике часто используют другое определение непрерывности функции в точке, равносильное данному.
Функция 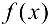 называется непрерывной в точке х0, если выполняются условия:
называется непрерывной в точке х0, если выполняются условия:
1) функция 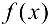 определена в точке
определена в точке 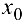 и ее окрестности;
и ее окрестности;
2) существуют конечные односторонние пределы
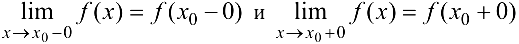
3) эти пределы равны между собой и равны значению функции в точке 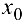 .
.
Укажем основные свойства непрерывных функций.
1. Простейшие элементарные функции (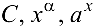 ,
, 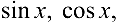
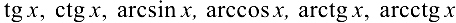 ) непрерывны во всех точках, где они определены.
) непрерывны во всех точках, где они определены.
2. Если функции 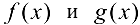 непрерывны в точке
непрерывны в точке 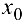 , то и функции
, то и функции 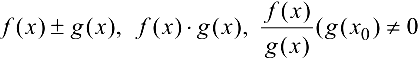 непрерывны в точке
непрерывны в точке 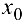 .
.
3. Если  непрерывна в точке
непрерывна в точке 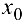 , а
, а 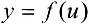 непрерывна в точке
непрерывна в точке 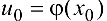 , то сложная функция
, то сложная функция 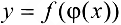 непрерывна в точке
непрерывна в точке 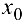 .
.
4. Если функция 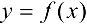 непрерывна на отрезке
непрерывна на отрезке 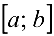 и возрастает (или убывает) на этом отрезке, то обратная функция
и возрастает (или убывает) на этом отрезке, то обратная функция 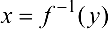 на соответствующем отрезке оси
на соответствующем отрезке оси 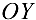 существует и является также непрерывной возрастающей (убывающей) функцией.
существует и является также непрерывной возрастающей (убывающей) функцией.
Точка 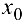 , в которой не выполняется хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции.
, в которой не выполняется хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции.
Если в точке 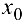 существуют конечные односторонние пределы
существуют конечные односторонние пределы 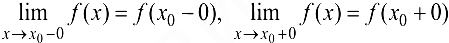 , такие что
, такие что 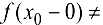
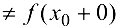 ., то
., то  называется точкой разрыва первого рода. Если хотя бы один из пределов
называется точкой разрыва первого рода. Если хотя бы один из пределов 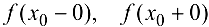 не существует или равен бесконечности, то точка
не существует или равен бесконечности, то точка 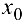 называется точкой разрыва второго рода. Если
называется точкой разрыва второго рода. Если 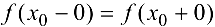 , по функция в точке
, по функция в точке 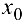 не определена или если,
не определена или если, 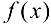 в точке
в точке 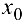 определена, но
определена, но 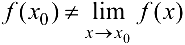 , то
, то 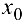 называется точкой устранимого разрыва.
называется точкой устранимого разрыва.
Возможно эта страница вам будет полезна:
| Решение задач по математическому анализу |
Пример 5.2.
Найти точки разрыва функции 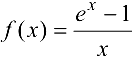 и определить их вид.
и определить их вид.
Решение:
Так как функции 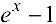 и
и 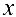 непрерывны, то непрерывным будет и их отношение
непрерывны, то непрерывным будет и их отношение 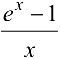 во всех точках, кроме точки
во всех точках, кроме точки 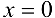 . При
. При 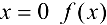 не определена, следовательно, разрывна. Так как
не определена, следовательно, разрывна. Так как 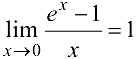 (см. п. 5.1 пример 12), то
(см. п. 5.1 пример 12), то 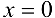 — точка устранимого разрыва. Если положить
— точка устранимого разрыва. Если положить 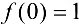 , то функция
, то функция
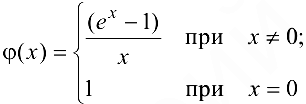
будет непрерывной при всех 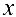 .
.
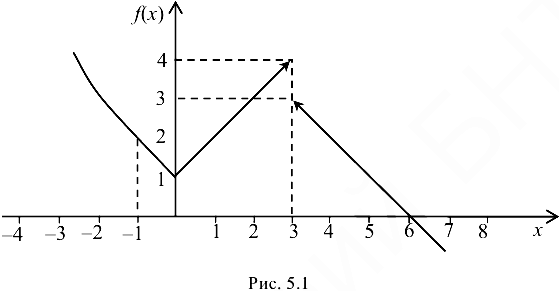
Пример 5.3.
Установить вид точек разрыва функции
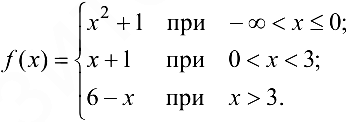
Решение:
Область определения функции 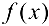 — вся числовая ось
— вся числовая ось 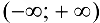 . Разрывы возможны только в точках
. Разрывы возможны только в точках 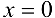 и
и 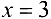 , в которых изменяется аналитическое задание функции. Найдем односторонние пределы в точке
, в которых изменяется аналитическое задание функции. Найдем односторонние пределы в точке 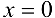 и значение функции в этой точке:
и значение функции в этой точке:
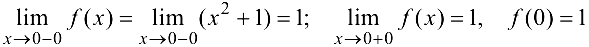
Следовательно, в точке 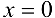 функция непрерывна.
функция непрерывна.
Рассмотрим точку 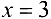 :
:
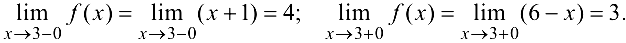
Так как эти пределы конечны но не равны между собой, то 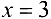 -точка разрыва первого рода. График функции
-точка разрыва первого рода. График функции 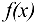 изображен на рис. 5.1.
изображен на рис. 5.1.
Пример 5.4.
Установить вид точек разрыва функции
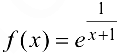
Решение:
Данная функция непрерывна всюду, кроме точки 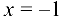 , в которой
, в которой  не определена.
не определена.
Поскольку
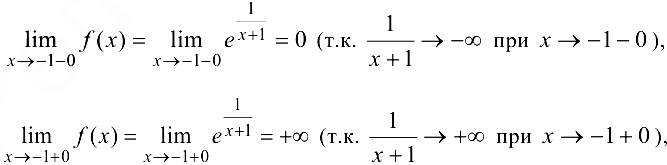
т.е. правосторонний предел бесконечен, то 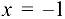 — точка разрыва второго рода.
— точка разрыва второго рода.
Дифференциальное исчисление функций одной переменной
Дифференцирование функций
Производной функции 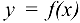 в точке
в точке 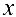 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
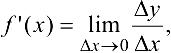
где 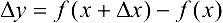 .
.
Производная обозначается 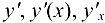 .
.
Правила дифференцирования функций. Пусть С — постоянная, а 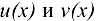 — дифференцируемые функции. Тогда
— дифференцируемые функции. Тогда 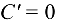 ,
,
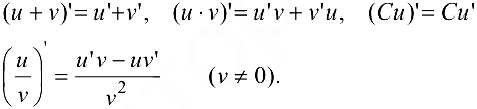
Производная сложной функции 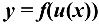 . Если функция
. Если функция 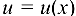 дифференцируема в точке
дифференцируема в точке 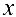 , а функция
, а функция 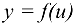 дифференцируемая в соответствующей точке
дифференцируемая в соответствующей точке 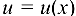 , то сложная функция
, то сложная функция 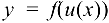 дифференцируема в точке х и ее производная равна
дифференцируема в точке х и ее производная равна
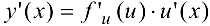
Таблица производных
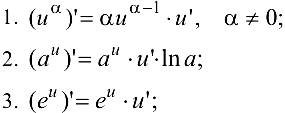
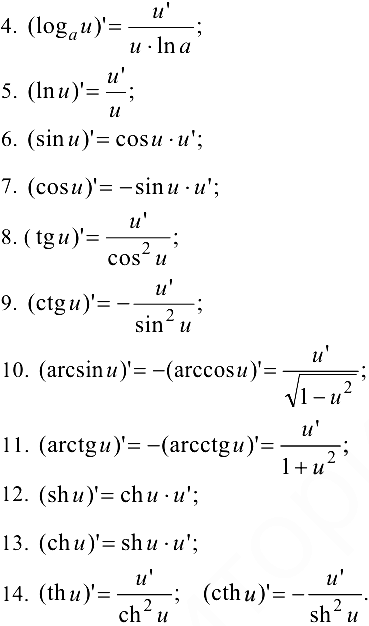
Функция 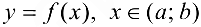 , неявно задана уравнением
, неявно задана уравнением  , если для всех
, если для всех  выполняется равенство
выполняется равенство 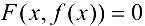 .
.
Для вычисления производной функции, заданной неявно, следует тождество 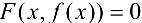 продифференцировать по
продифференцировать по  (рассматривая левую часть как сложную функцию от
(рассматривая левую часть как сложную функцию от  ), а затем полученное уравнение решить относительно
), а затем полученное уравнение решить относительно 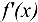
Пример 6.1.
Найти производную показательно-степенной функции
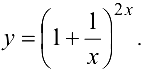
Решение:
Логарифмируя, а затем дифференцируя левую и правую части, получим
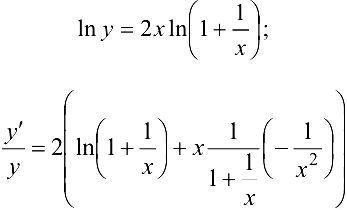
Умножая обе части равенства на у, имеем:
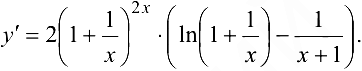
Пример 6.2.
Найти производную функции 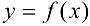 , заданной неявно уравнением
, заданной неявно уравнением 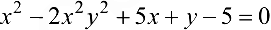 .
.
Решение:
Дифференцируя по 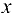 тождество
тождество 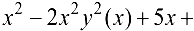
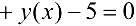 , получим
, получим 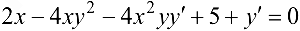 . Выражая
. Выражая 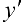 из этого равенства, находим:
из этого равенства, находим:
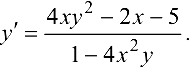
Дифференциал 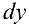 функции
функции 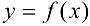 равен произведению ее производной па приращение
равен произведению ее производной па приращение 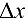 независимой переменной:
независимой переменной: 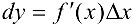 или
или 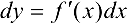 .
.
При достаточно малых 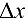 имеет место приближенная формула
имеет место приближенная формула 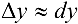 , т.е.
, т.е. 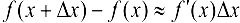 или
или 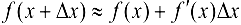 .
.
Возможно эта страница вам будет полезна:
| Математический анализ помощь онлайн |
Пример 6.3.
Найти приближенное значение объема шара, радиус которого равен 1,02 м.
Решение:
Воспользуемся формулой 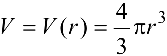 . Тогда
. Тогда 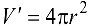 . Полагая
. Полагая 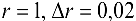 , получим
, получим 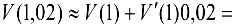
Производные и дифференциалы высших порядков. Дифференцирование функций, заданных параметрически
Производной второго порядка функции 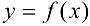 называется производная от ее производной
называется производная от ее производной 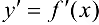 , т.е.
, т.е. 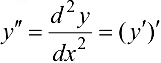 .
.
Аналогично определяются производные более высоких порядков  .
.
Дифференциалы высших порядков функции 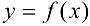 (
(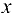 — независимая переменная) вычисляются по формулам
— независимая переменная) вычисляются по формулам
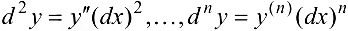
Если функция 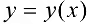 задана параметрически соотношениями
задана параметрически соотношениями 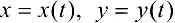 , причем
, причем 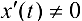 , то ее первая
, то ее первая 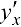 и вторая
и вторая 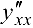 производные находятся по формулам:
производные находятся по формулам:
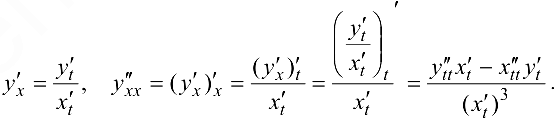
Пример 6.4.
Найти выражение для производной 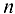 -го порядка функции
-го порядка функции 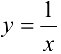 .
.
Решение:
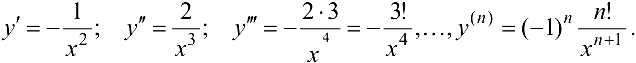
Пример 6.5.
Найти производную 2-го порядка от функции 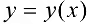 , заданной неявно уравнением
, заданной неявно уравнением 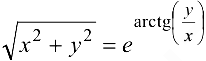 .
.
Решение:
По правилу дифференцирования функции, заданной неявно, получаем:
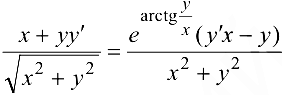
Отсюда, используя равенство 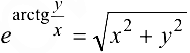 , имеем:
, имеем:
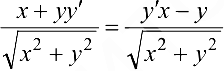 или
или 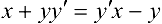
Следовательно, 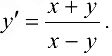 .
.
Дифференцируя последнее равенство и используя найденное для 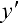 выражение, получим:
выражение, получим:
Возможно эта страница вам будет полезна:
| Математический анализ для 1 курса |
Пример 6.6.
Найти производную 2-го порядка функции, заданной параметрически: 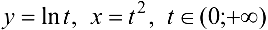 .
.
Решение:
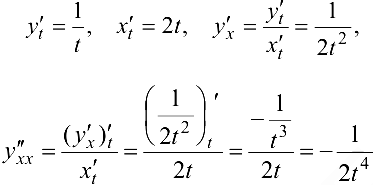
Пример 6.7.
Найти дифференциалы 1-го, 2-го, …, 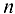 -го порядков функции
-го порядков функции 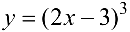 .
.
Решение:
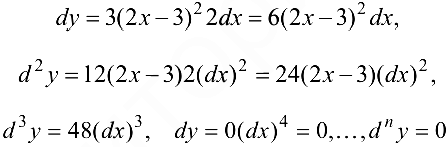
Приложение теорем Ролля, Лагранжа, Коши. Правило Лопиталя
- Теорема Ролля. Если функция
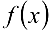 непрерывна на отрезке
непрерывна на отрезке 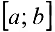 , дифференцируема на интервале
, дифференцируема на интервале 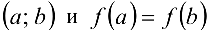 , то существует хотя бы одна точка
, то существует хотя бы одна точка 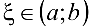 такая, что
такая, что 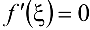 .
. - Теорема Лагранжа. Если функция
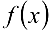 непрерывна на отрезке
непрерывна на отрезке 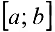 и дифференцируема на интервале
и дифференцируема на интервале 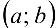 , то существует точка
, то существует точка 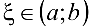 такая, что
такая, что 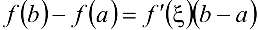 (формула Ла-
(формула Ла-
гранжа). - Теорема Коши. Если функции ,
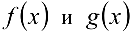 непрерывны на отрезке
непрерывны на отрезке 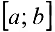 , дифференцируемы на интервале
, дифференцируемы на интервале 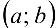 и
и 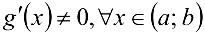 , то существует точка
, то существует точка 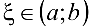 такая, что
такая, что 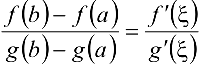 (формула Коши).
(формула Коши).
Пример 6.8.
Доказать, что уравнение 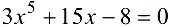 имеет только один действительный корень.
имеет только один действительный корень.
Решение:
Поскольку функция 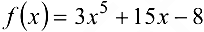 непрерывна и на концах отрезка
непрерывна и на концах отрезка 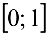 принимает значение разных знаков
принимает значение разных знаков 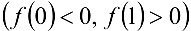 -, то по первой теореме Больцано Коши на интервале
-, то по первой теореме Больцано Коши на интервале 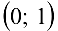 уравнение
уравнение 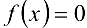 имеет корень. Предположим, от противного, что это уравнение имеет два действительных корня
имеет корень. Предположим, от противного, что это уравнение имеет два действительных корня 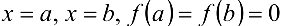 .
.
Тогда по теореме Ролля па интервале 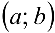 существовала бы точка
существовала бы точка 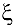 , в которой
, в которой 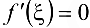 . Но
. Но 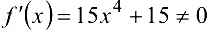 при действительных
при действительных 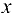 . Полученное противоречие доказывает, что действительный корень — единственный.
. Полученное противоречие доказывает, что действительный корень — единственный.
Пример 6.9.
Используя формулу Лагранжа, доказать неравенство 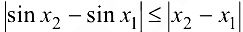 .
.
Решение:
Функция 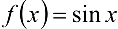 удовлетворяет условиям теоремы Лагранжа на любом отрезке
удовлетворяет условиям теоремы Лагранжа на любом отрезке 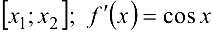 . Поэтому
. Поэтому 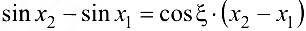 . Отсюда, учитывая, что
. Отсюда, учитывая, что 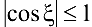 , имеем
, имеем 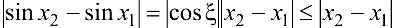 .
.
Пример 6.10.
Написать формулу Коши и найти значение 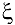 , для функций
, для функций 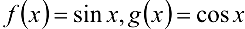 на отрезке
на отрезке 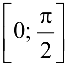
Решение:
Все условия теоремы Коши выполнены: 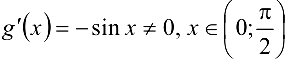 . Поэтому
. Поэтому
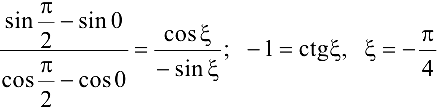
Правило Лопиталя (раскрытие неопределенностей 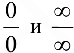 ).
).
Пусть 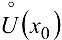 — окрестность точки
— окрестность точки 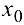 с выброшенной точки
с выброшенной точки 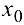 .
.
Теорема. Пусть функции 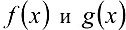 дифференцируемы на
дифференцируемы на 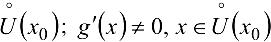
Если 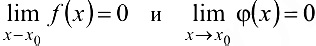 (или
(или 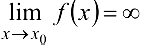 и
и 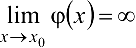 , то
, то 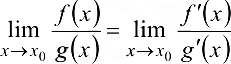 при условии, что существует предел отношения производных.
при условии, что существует предел отношения производных.
Замечания:
1. Аналогичная теорема справедлива и в случае 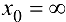
2. Если частное 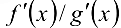 в точке
в точке 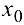 также есть неопределенность вида
также есть неопределенность вида 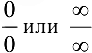 и производные
и производные 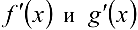 удовлетворяют соответствующим условиям, то можно перейти к отношению вторых производных и т.д.
удовлетворяют соответствующим условиям, то можно перейти к отношению вторых производных и т.д.
3. Неопределенности вида 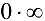 или
или  алгебраическими преобразованиями функции приводятся к неопределенности вида
алгебраическими преобразованиями функции приводятся к неопределенности вида 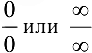 далее применяется правило Лопиталя.
далее применяется правило Лопиталя.
4. В случае неопределенности вида 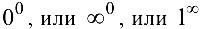 следует прологарифмировать функцию и предварительно найти предел ее логарифма.
следует прологарифмировать функцию и предварительно найти предел ее логарифма.
Возможно эта страница вам будет полезна:
| Сборники и решебники задач по математическому анализу |
Пример 6.11.
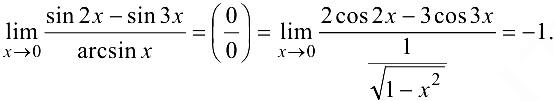
Пример 6.12.
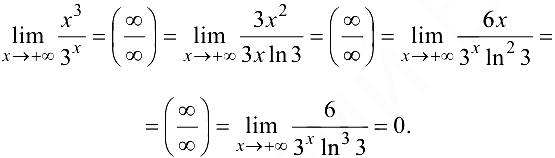
Пример 6.13.
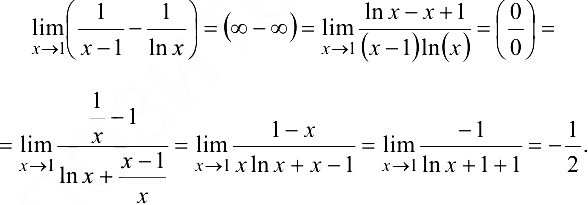
Пример 6.14.
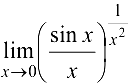 Здесь неопределенность вида
Здесь неопределенность вида 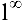 .
.
Обозначим 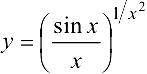 . Логарифмируя и применяя правило Лопиталя, получим
. Логарифмируя и применяя правило Лопиталя, получим
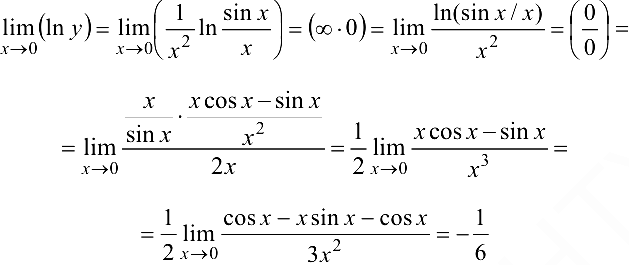
(здесь дважды использован предел 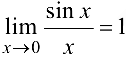 ).
).
Поскольку  .
.
Формула Тейлора и ее приложения
Если функция 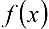 дифференцируема
дифференцируема 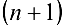 раз в окрестности
раз в окрестности 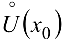 точки
точки 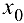 , то для любого
, то для любого 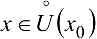 имеет место формула Тейлора
имеет место формула Тейлора 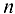 -го порядка
-го порядка
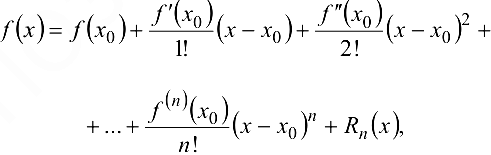
где 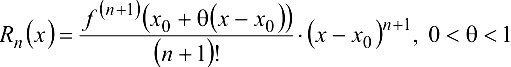 — остаточный член в форме Лагранжа.
— остаточный член в форме Лагранжа.
Приведем разложения некоторых функций по формуле Тейлора при 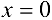 :
:
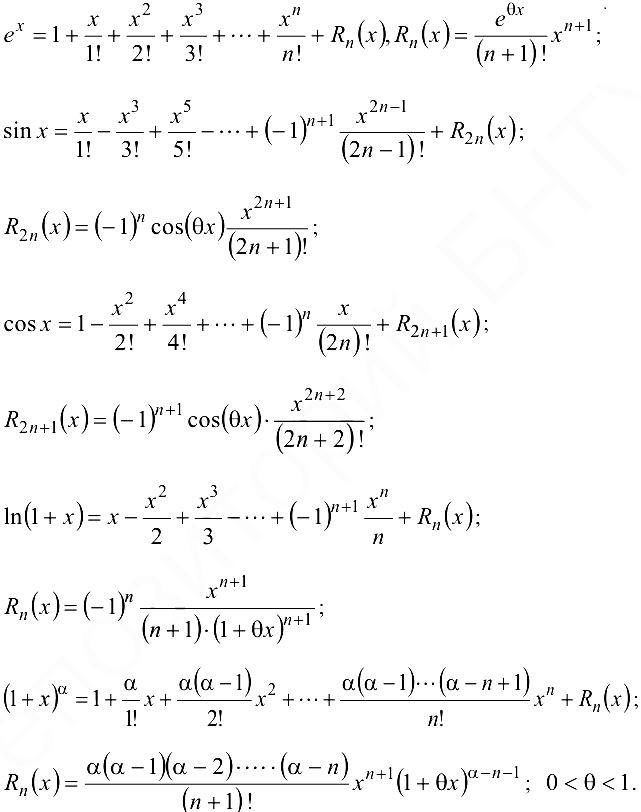
Остаточный член формулы Тейлора может быть представлен в форме Пеано: 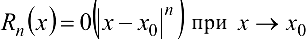 .
.
Пример 6.15.
Разложить многочлен 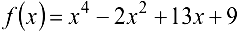 по степеням двучлена
по степеням двучлена 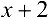 .
.
Решение:
Поскольку 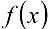 — многочлен 4-й степени, то
— многочлен 4-й степени, то 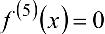 и формула Тейлора при
и формула Тейлора при 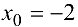 имеет вид
имеет вид
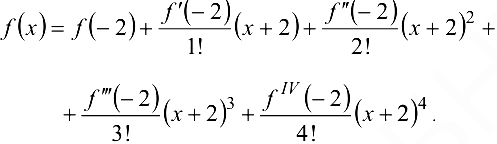
Подставляя в эту формулу значения 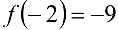 ,
,
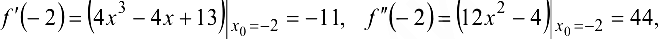
 , получим
, получим
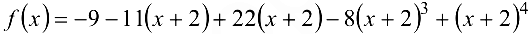
Пример 6.16.
Написать формулу Тейлора 3-го порядка для функции 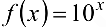 в точке
в точке 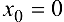 .
.
Решение:
Имеем
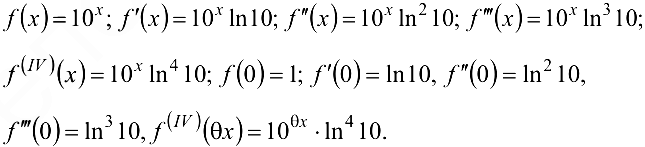
По формуле Тейлора получаем
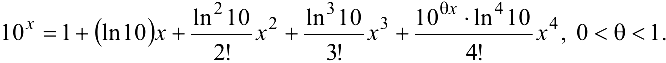
Пример 6.17.
Вывести приближенную формулу 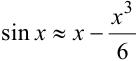 и оценить ее точность при
и оценить ее точность при 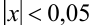 .
.
Решение:
Запишем формулу Тейлора 4-го порядка для функции 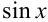 в точке
в точке 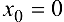 :
:
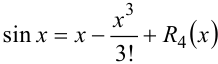 , где
, где 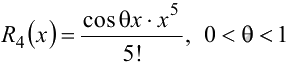 .
.
При  имеем
имеем 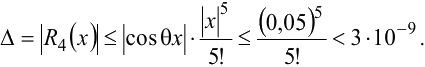
Поэтому 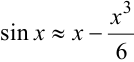 с точностью
с точностью 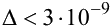
Пример 6.18.
Вычислить 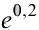 с точностью до
с точностью до 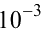 .
.
Решение:
Формула Тейлора для функции 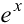 имеет вид
имеет вид
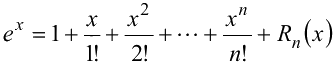
где 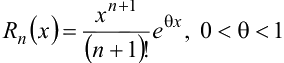 .
.
Полагая 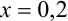 , получим:
, получим:
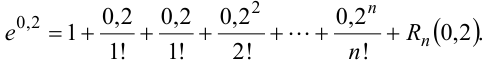
где 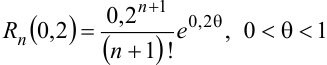 .
.
Так как 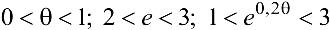 , то
, то
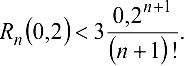
Определим наименьшее значение 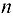 так, чтобы выполнялось неравенство
так, чтобы выполнялось неравенство 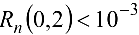 .
.
Если 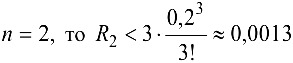 , а если
, а если 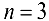 , то
, то 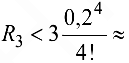
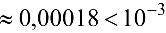 Поэтому
Поэтому 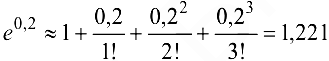 с точностью до
с точностью до 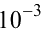 .
.
Пример 6.19.
Вычислить 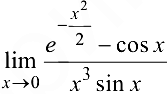 .
.
Используем формулу Тейлора с остаточными членами в форме Пеано:
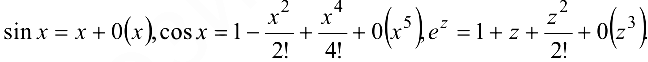
Из последней формулы при 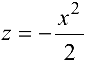 получим
получим
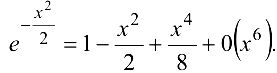
Искомый предел может быть переписан в виде
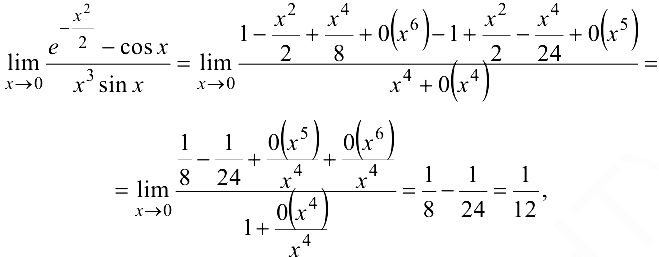
(поскольку 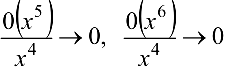 ) при
) при 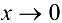 ).
).
Применение дифференциального исчисления для исследования функций и построения их графиков
Исследование функций на экстремум. Выпуклость и вогнутость кривой, точки перегиба. Асимптоты
Если существует окрестность 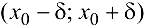 точки
точки 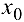 такая, что для всякой точки
такая, что для всякой точки 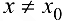 этой окрестности выполняется неравенство
этой окрестности выполняется неравенство 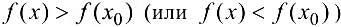 , то точка
, то точка 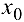 называется точкой минимума (максимума) функции
называется точкой минимума (максимума) функции 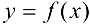 .
.
Точки минимума и максимума функции называются ее точками экстремума.
Теорема 1 (необходимое условие экстремума). Если 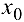 -точка экстремума функции
-точка экстремума функции 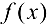 , то
, то 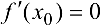 или
или 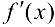 не существует (
не существует (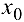 — критическая точка этой функции).
— критическая точка этой функции).
Теорема 2 (первое достаточное условие экстремума). Пусть функция 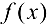 дифференцируема в некоторой окрестности (
дифференцируема в некоторой окрестности (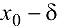 ;
; 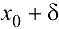 ) критической точки
) критической точки 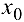 , за исключением, быть может, самой этой точки. Если при этом в интервалах
, за исключением, быть может, самой этой точки. Если при этом в интервалах 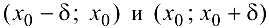 производная
производная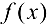 имеет противоположные знаки, то
имеет противоположные знаки, то 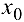 — точка экстремума, причем если
— точка экстремума, причем если 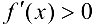 при
при 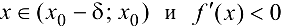 при
при 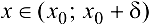 , то
, то 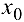 — точка максимума. Если же
— точка максимума. Если же 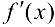 при
при 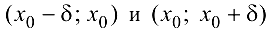 сохраняет знак, то точка
сохраняет знак, то точка 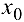 не является точкой экстремума.
не является точкой экстремума.
Теорема 3 (второе достаточное условие экстремума). Пусть 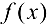 дважды дифференцируема и
дважды дифференцируема и 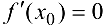 . Если
. Если 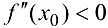 , то
, то 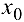 — точка максимума функции
— точка максимума функции 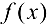 , если
, если 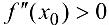 , то
, то 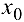 -точка минимума. Если же
-точка минимума. Если же 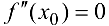 , то требуются дополнительные исследования.
, то требуются дополнительные исследования.
Если па интервале 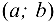 всякая касательная располагается выше (ниже) дуги кривой, то график дифференцируемой функции на этом интервале называется выпуклым (вогнутым).
всякая касательная располагается выше (ниже) дуги кривой, то график дифференцируемой функции на этом интервале называется выпуклым (вогнутым).
Если 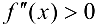 на интервале
на интервале 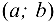 , то график функции является вогнутым па этом интервале; если же
, то график функции является вогнутым па этом интервале; если же 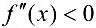 , то график функции — выпуклый на
, то график функции — выпуклый на 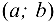 .
.
Точка 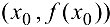 , при переходе через которую направление выпуклости графика функции меняется на противоположное, называется точкой перегиба.
, при переходе через которую направление выпуклости графика функции меняется на противоположное, называется точкой перегиба.
Теорема 4 (необходимое условие точки перегиба). Если 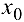 — абсцисса точки перегиба графика функции
— абсцисса точки перегиба графика функции 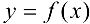 , то
, то 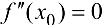 или
или 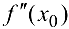 не существует.
не существует.
Теорема 5 (достаточное условие точки перегиба). Пусть функция 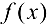 дважды дифференцируема в некоторой окрестности
дважды дифференцируема в некоторой окрестности 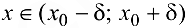 точки
точки 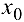 , в которой
, в которой 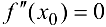 или
или 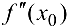 не существует. Если при этом в интервалах
не существует. Если при этом в интервалах 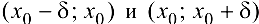 вторая производная
вторая производная 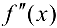 имеет противоположные знаки, то
имеет противоположные знаки, то 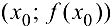 — точка перегиба.
— точка перегиба.
Прямая 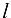 называется асимптотой графика функции
называется асимптотой графика функции 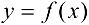 , если расстояние от точки
, если расстояние от точки 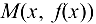 графика функции до прямой
графика функции до прямой 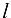 стремится к пулю при неограниченном удалении точки М от начала координат.
стремится к пулю при неограниченном удалении точки М от начала координат.
Для существования вертикальной асимптоты 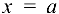 необходимо и достаточно, чтобы хотя бы один из односторонних пределов
необходимо и достаточно, чтобы хотя бы один из односторонних пределов 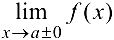 был равен бесконечности.
был равен бесконечности.
Для существования наклонной асимптоты 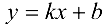 необходимо и достаточно существование двух пределов
необходимо и достаточно существование двух пределов
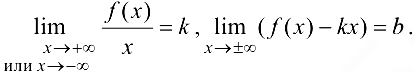
Пример 7.1.
Для функции 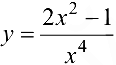 найти интервалы возрастания и убывания и точки экстремума.
найти интервалы возрастания и убывания и точки экстремума.
Решение:
Находя производную 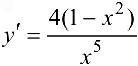 и приравнивая ее нулю, получаем
и приравнивая ее нулю, получаем 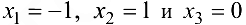 (при
(при 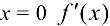 не существует). Эти точки разбивают область определения функции на интервалы монотонности. Результаты исследования удобно представить в виде таблицы.
не существует). Эти точки разбивают область определения функции на интервалы монотонности. Результаты исследования удобно представить в виде таблицы.

Следовательно, 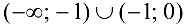 — интервалы возрастания функции;
— интервалы возрастания функции; 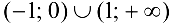 — интервалы убывания функции;
— интервалы убывания функции; 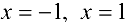 — точки максимума. Точек минимума нет.
— точки максимума. Точек минимума нет.
Пример 7.2.
Для графика функции 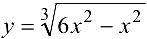 найти интервалы выпуклости и вогнутости и точки перегиба.
найти интервалы выпуклости и вогнутости и точки перегиба.
Решение:
Находим вторую производную 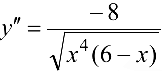 .
.
Критическими точками второй производной являются точки 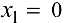 и
и 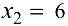 ( в этих точках
( в этих точках 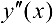 не существует). Они разбивают область определения функции на три интервала, на которых сохраняется направление выпуклости или вогнутости. Результаты исследования удобно представить в виде таблицы.
не существует). Они разбивают область определения функции на три интервала, на которых сохраняется направление выпуклости или вогнутости. Результаты исследования удобно представить в виде таблицы.

Таким образом, 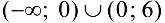 — интервалы выпуклости графика функции;
— интервалы выпуклости графика функции; 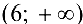 — интервал вогнутости графика функции; (6, 0) -точка перегиба.
— интервал вогнутости графика функции; (6, 0) -точка перегиба.
Пример 7.3.
Найти асимптоты графика функции 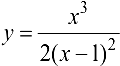 .
.
Решение:
Прямая 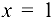 является вертикальной асимптотой, так как
является вертикальной асимптотой, так как
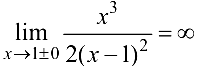
Наклонную асимптоту ищем в виде 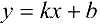 ,
,
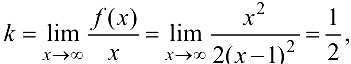
где 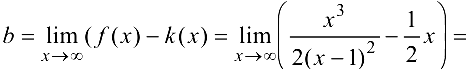
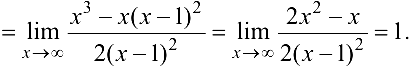
Поэтому прямая 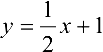 — наклонная асимптота.
— наклонная асимптота.
Исследование функций и построение их графиков
Исследование функций и построение их графиков удобно выполнять по следующей схеме.
- Найти область определения функции.
- Выяснить, является ли функция четной, нечетной, периодической.
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Установить интервалы монотонности функции. Найти точки экстремума функции, вычислить значения функции в этих точках.
- Определить интервалы выпуклости и вогнутости графика функции, точки перегиба.
- Используя результаты проведенного исследования, построить график функции. При необходимости уточнения отдельных участков кривой можно вычислить координаты нескольких дополнительных точек (в частности, координаты точек пересечения графика с осями координат).
Кстати теория из учебников по математическому анализу тут.
Пример 7.4.
Исследовать функцию 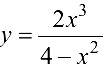 и построить ее график.
и построить ее график.
Функция определена и непрерывна на всей оси, кроме точек 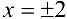 .
.
Функция нечетная, так как 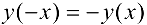 , ее график симметричен относительно начала координат, поэтому достаточно исследовать функцию для
, ее график симметричен относительно начала координат, поэтому достаточно исследовать функцию для 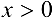 . Прямые
. Прямые 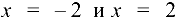 являются вертикальными асимптотами, поскольку
являются вертикальными асимптотами, поскольку 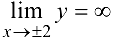 . Найдем наклонные асимптоты
. Найдем наклонные асимптоты 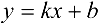 :
:
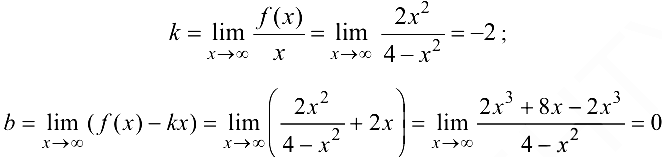
Следовательно, 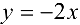 — наклонная асимптота.
— наклонная асимптота.
Производная функции 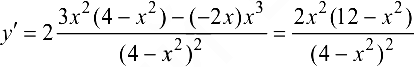
обращается в нуль при 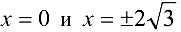 .
.
Вторая производная
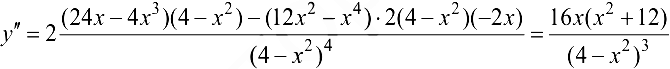
обращается в нуль при 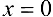 .
.
Составим таблицу

Следовательно, 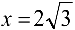 — точка максимума,
— точка максимума, 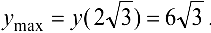 . В силу нечетности имеем:
. В силу нечетности имеем: 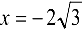 — точка минимума
— точка минимума 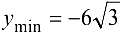 . Поскольку
. Поскольку 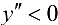 при
при 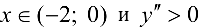 при
при 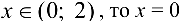 — абсцисса точки перегиба, 0(0;0) — точка перегиба.
— абсцисса точки перегиба, 0(0;0) — точка перегиба.
Используя полученные данные, строим график функции (рис. 7.1).