Оглавление:




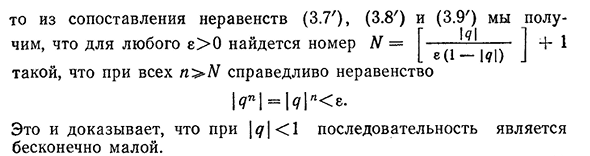

Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
- Ограниченная, неограниченная, бесконечно малая, бесконечно большая последовательность. Множество всех элементов произвольной последовательности{CP}образует множество чисел. Начиная с понятия ограниченной вершины, дна или обеих сторон множества, оно становится определением: О П Р Е Д Е Л Е Н и Е1.
Последовательность{ХП}, если существует реальная м (реальная ПГ), таких, что каждый элемент этой последовательности удовлетворяет неравенству СР СР<, О Г-Р А Н И ч н о м ы р е х г(С Н им(НР^Т)). В этом случае число м(число Т)называется Н У Ю(Н И Ж Н Е Г В Г)последовательность{ХР}, неравный знак Х»<Л1(х»Т), У С Л О В и Е М О Г Р А Н И Ч Е Н О О Н). Любой верхний ограниченный массив имеет бесконечное множество верхних граней,
и при условии верхнего ограниченного массива x ‘ и=, любое число M * больше Mявляется Людмила Фирмаль
верхней гранью. О П Р Е Д Е Л Е Н и Е2. Если последовательность{CP}заключена как выше, так и ниже, т. е. есть dwa70GL, то ogr a n I h e n N o y s o b e i x s t O R o n(или просто o g 3. Теория пределов Действительные числа M и t таковы, что каждый элемент этой последовательности xn удовлетворяет неравенству t^.числа xn< — M (3.3) m и M называются нижним и верхним концами последовательности{xn}, а неравенство(3.3) называется y C l O V, а определения E m o g R A n и H N приблизительно T и N N и ограничение последовательности требуют меньше t и эффективного M, так что
неравенство даже пара пар существует Заметим, что последовательность {% » } ограничена только в том случае, если существует положительное вещественное A, такое, что каждый элемент последовательности xn удовлетворяет неравенству\xn\<.A. (3.4) на самом деле, если все элементы CP удовлетворяют неравенству (3.4), если вы поставите PG=—A, M=+L, вы увидите, что CP удовлетворяет неравенству (3.3). И наоборот, если каждый элемент x n удовлетворяет неравенству (3.3), то если обозначить наибольший из|t|и|M|, то можно сказать, что x n удовлетворяет неравенству (3.4). В соответствии с ограниченными условиями, принятыми в
- определении 2 и формате (3.4) ограниченных массивов, можно определить понятие ограниченных массивов. Последовательность {% » } называется N E O g R a n I h n N o y, если существует хотя бы один элемент последовательности xn, удовлетворяющий неравенству для любого положительного вещественного A. *Независимо от того, насколько большой мы берем это число. С > Л. (3.5) С точки зрения этого определения, последовательность, ограниченная только верхней или нижней частью, является неограниченной. Так, например, последовательность 1, 2, 1, 4,…1, 2 часа дня… Какое бы положительное вещественное число A мы ни взяли, в этой последовательности есть элемент, имеющий четное число,
удовлетворяющее неравенству(3.5).§1. Последовательность и ее пределы 71 Каждый элемент в этой последовательности удовлетворяет неравенствам t<0 и L1>1 (3.3). Теперь введем понятие последовательности бесконечно малого и бесконечно малого. О П Р Е Д Е Л Е Н и Е3. Последовательность{CP}называется besk o n e h n o b o l W o y, положительное вещественное число * a имеет число N, t, и для всех n’-1>N элементы CP этой последовательности неравны. *Независимо от того, насколько большой мы берем это число. **
Так как это число N. вообще говоря, зависит от, то иногда пишется:#=y(L). *** Бесконечные малые элементы последовательности, мы будем Людмила Фирмаль
стремиться указать греческие буквы. ****СК о л л л ь м мы бы взяли этот номер. *Это число, вообще говоря, зависит от e, поэтому иногда пишется:# = LG (e). Определение бесконечно большой последовательности должно удовлетворять всем элементам последовательности, начинающейся с определенного числа D, при любом L>0 неравенстве (3.5), и должно быть определено неограниченное число последовательностей. Но не все неограниченные массивы бесконечно велики. Например, приведенная выше последовательность 1, 2, 1, 4,…, 1, 2p, является неограниченным и не бесконечно большим, но в случае любого L>1 неравенство (3.5) не имеет места для элементов CP с любым нечетным числом P. О п р ЕД е л я Е4. Последовательность{a»}* * * называется b e C K o n e h n o m A lo y, и для любого
положительного действительного числа e* * если есть число N, ta * K * o * y, то все n^D в этой последовательности. |И I / Д2…. РАЗНОСТЬ ПОТЕНЦИАЛОВ.,. Б ЕСК о н н о л ь ш о й при]у|>1 и Б Е С К о н е ч н о м А Л О й пр У<1. Сначала предположим|^ / >1. Тогда|d / =1+6, где 6>0. Используя двоичную формулу Ньютона, вы можете написать|^ / L’=(1+6) 7U=1+L^6+(положительный член). Следовательно, неравенство|<7г > 6#. (3.7) 72 Глава 3. Теория пределов Зафиксируйте любое положительное число A и выберите такое число N, где неравенство 6#>L истинно. (3.8) Для любого L>0 убедитесь, что вы можете выбрать число Y, удовлетворяющее неравенству (3.8). Символ[x]согласен обозначать целочисленную часть положительного вещественного X.
Поскольку неравенство (3.8) эквивалентно неравенству N>7 -, O Таким образом, это неравенство, безусловно, удовлетворяет числу D, выбранному из примечаний из|<7|>1, и всем n>LA из природы произведения действительного числа Но / ? / -1 Условие N — [- y+1=+1. Если мы сравним 1I>|<7G-(3.9) неравенства (3.7), (3.8) и (3.9), то для любого L>0 получим фигуру LA=G—1+1: I1Ла |<7″| = |<7|»>л. Это доказывает, что последовательность|<7|>1 ({<7″) бесконечно велик. Теперь рассмотрим случай| < 71<1. В этом случае вам нужно доказать, что последовательность{CPU}бесконечно мала. За исключением незначительных случаев<7=0, пусть— — — =1+6, где W 6 > 0. Если вы используете биномиальное распределение Ньютона, как указано выше, вы получаете неравенства вместо(3.7) — ^>6^или|<7G< — A_.
(3.7′)зафиксируйте любое положительное число e и выберите число N таким образом, чтобы неравенство было истинным (3-8′) Для того, чтобы неравенство (3.8′) было равно неравенству N>-7 -, для выбора указанного числа достаточно поставить EO N=G-t-1 + 1 = [ —— —— | + 1. Далее, с тех пор, спасибо Б ЭБ] [Е(1-И1) ] Для всех| < 71<1 и > LA, когда неравенство истинно, свойство произведения действительного числа И Я< / <7|. (3.9′)§1. Последовательность и ее пределы 73 м_ -|? | ) +1 Тогда неравенство(3.7’)、(3.8’)、и из сравнения (3.9′), для любого e>0, мы получаем число n=—. Восемь. ( Все неравенства N^S являются|<7″| = 1<7|p<e. Это доказывает, что последовательность бесконечно мала при|<7 / <1.
Смотрите также:
Решение задач по математическому анализу
