Оглавление:

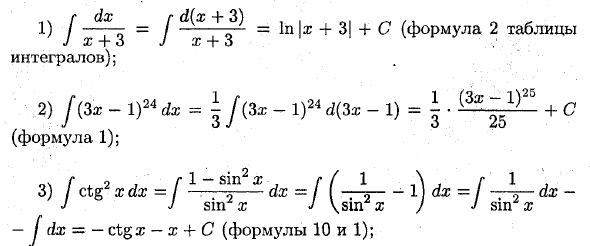

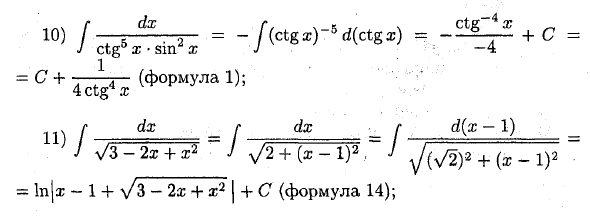

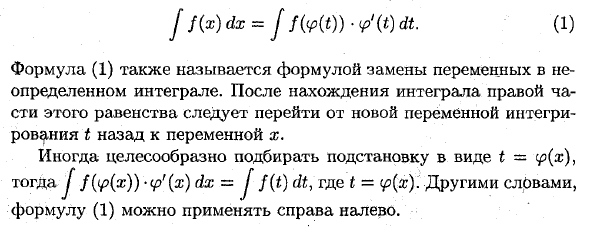

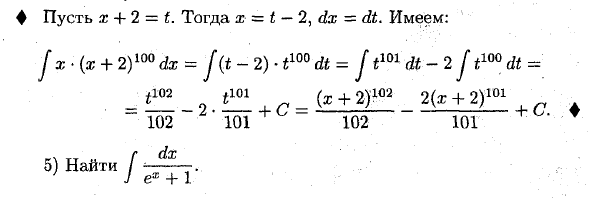

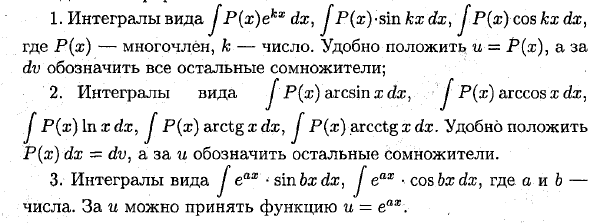
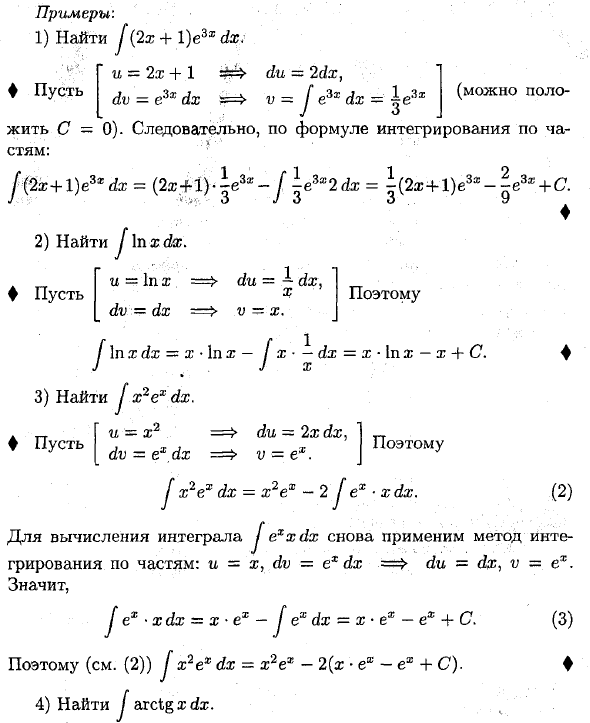
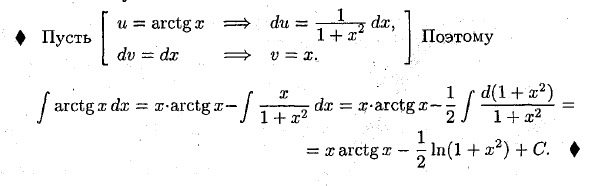
Основные методы интегрирования
- Основное) Метод интеграции г Я •, ‘4 1. Метод прямой интеграции 4 <V. , (. Метод интегрирования, который уменьшает применение определенных интегральных и неопределенных интегральных свойств при одном и том же $$ образовании подынтегрального выражения (или выражения) к одному или нескольким табличным интегралам, называется прямым интегрированием.
(операция «поставить под производным знаком»): du = d (u + a), a — это число, du — d (au), φО — числовое значение, и И ■ du = -d (u2)) cos и du = d (sintt), sin udu = —d (cosw), -du = d (lnu) и = д (тгу). cos2 и Вообще, f ‘(u) du = d (f (u)), эта формула очень часто используется для интегральных вычислений.
При уменьшении этого интеграла до табличного интеграла часто используется следующее производное преобразование Людмила Фирмаль
Пример:Интегрирование в виде JP (x) exx dx, JP (x) — син kxdx> JP (x) cos kx dx} Где P (x) — многочлен, а k — число. Полезно поставить u = P (x) и dv и показать все остальные факторы. 2. Интегрирование вида J P (x) arcsin x dx, J P (x) arccosxdz, JP (x) Ln x dx, JP (x) арктан x dxy J P (x) arcctg x dx. Удобно положить P (x) dx = dv и указать остальные факторы. 3. J eax-sin bxdx, интеграция формата ^ eax • cosbxdx. а и 6 являются числами. Можно взять функцию u = eax.
Пример: 1) Найти J (2x + 1) e3d dx: И = 2.t + 1 du = 2 dx} dv = eZx dx v = J e3xdx = | e3x Live C = 0). Поэтому с интегрированной формулой частей: J (2x + 1) eZx dx = (2® + 1) — | e3 * -y | e3yag2Ag = ^ (2×4-1) e3 * — + 2) Найти J \ nxdx. И -х => ду = ^ дх, ^ (2) v-х. J \ nxdx = x ‘\ nx-J x • -dx = x-in x-x + C 3) Найти J x2ex dx. Oh Gu-x1 => du = 2xdx, I ♦ ^ CTb [dv = ex, dx => v = ex. J P ° это J x2ex dx = x2ex-2 jex -xdx. Чтобы вычислить интеграл J exxdx, примените метод частичного интегрирования еще раз: u = i, dv = e * dx => du = dx, v для ex означает J ex-xdx = x> ex-J ex dx = x ex-ex + C (3) Поэтому (см. (2)) J x2ex dx = sV-2 (x • e * -ex + C). ♦ 4) Найти j arctgzdx. (Вы можете ♦ сделать
| Неопределенный интеграл | Интегрирование тригонометрических функций |
| Таблица основных интегралов | Интегрирование иррациональных функций |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- du =. -l dx, 1 -fx2 V = X. и = arctg i dv-dx так ♦ сделать G ‘, G®. 1 г с / (1 ч-w2) / arctg xarr = cn-arctgx- / — dx = x-arctgx ~ — / — Y l + r 271 + a; = gg arctgt — ln (l + x2) + C 1) f- = f ——— = In \ x + 31 + C (Таблица Jx- + 6 J x + S Уравнение 2 Интеграция); 2) J (3s-l) 24 dx = \ j {3 * -l) «d (3x-1) = 1 • (3a? ~ 1) 25 + C (уравнение 1); / г 1 до «sin2 x g (1 \ p) ctg2 xdx = — ^ — ~ dx = I [—5 — 1) dx = —o— dx- J sinx J \ sinx J J грех a; -f dx = -ctg a; -x -f C (уравнения 10 и 1);
^ f dx 1 r d (V3-x) 1 UD ( 4) /// = — 7 = /. -: — = • arcsm —-— 4-С ‘lyr ^ Oz J y (2) 2 . х) 2 V3 2 (Формула 13); 5) J sin2 6x dx = ^ J (1-cos 12x) dx = ^ J dx- ~ J cos 12x dx = ~ \ x ~ \ f cos d (12x) ‘J2 = ~ s * n + & (Формула 1 И 6); 61 G dx = 1 G «0- + 2) =} J {x-1) (x + 2) 3 J {x-1) (x + 2) 1 г х-я 1 г х + 2 _1 Г д (х -ф 2) «~» ~ S / (x-1) (x + 2) +3 Дж (x-1) (x + 2) ~ 3 J x + 2 + 7) [tg и du = f c = -f ^ cos = -в I cos u I + С (вывод УУ.cosuУcos.14 Формула 7); nN g du g cos2% + sin2 y, / -cos2 ^ 2 sin% cos g du = J 2sW <4cosZdu + От 2 до 2 + j sin21 2 грех я потому что я I IX I cos- + C = In я Грех 2 потому что 2 (£) =. 14 Грех — 42/2 Я -B C = In tg- + C (вывод уравнения 11); Это я 9) J x (x + 2) 9 dx = J (x + 2-2) (x 4-2) 9 dx = J (x + 2) 10 dx -2 J (x + 2) 9 dx = J ( xf 2) 10 d (x + 2) -2 | (x + 2) 9 d (x + 2) = -2 (X4) Q2) 1 ° C (формула 1);
10) [dx, 2 = -f (ctg x) 5d (ctgx) = + C = Y ctg ° z siir i y -4 = C + 4ctg4.T (Ф ° Рмула dx r dx g d (x-1) U) F, Ax-F. х — [_ J V3-2x + x’2 J V2 + (x-1) 2 J + {x _ 1} 2 = jx-1 + \ / 3-2x + x2 I + С (формула 14); 12) [(4 * 3 — V + = 4 f x3 dx- | [Щ — J \ cos2 2x / J 2 /; cos2 2nd г 5 31 «» ®-1 -31 «* d (l-x) = X4 — tg2x- + C (формулы 1, 9, 3); 13) x3 • Vl + * 2 dx = y * (l + i2) * • ^ • (x2 + 1-l) dx = Как видите, вычисление интеграла требует так называемого «индивидуального подхода к каждому интегралу».
2. Метод интегрирования путем подстановки (подстановка переменных) Метод интегрирования путем замены заключается во введении новой интеграционной переменной (т.е. замены). В этом случае данная интеграция сводится к новой интеграции, которая является табличной или сводится к ней (в случае «успешной» замены). Нет общего способа выбрать замену. Способность правильно оценивать замену приобретается практикой.
Значительное количество упражнений приведет к правильным навыкам. Людмила Фирмаль
Предположим, нам нужно вычислить интеграл J f (x) dx. Сделайте замену x = tp (t). Где <p (t) — функция с непрерывным дифференцированием. Далее, dx = ip ‘(t) dt и на основе инвариантного свойства интегральной формулы неопределенного интеграла получить интегральную формулу путем подстановки.
J / <«) dx = J / („ («)) ■ V ‘(t) dt. (1) Уравнение (1) также называется уравнением подстановки переменных для неопределенного интегрирования. После нахождения интеграла в правой части этого уравнения нам нужно вернуться от новой интегральной переменной t к переменной x. В некоторых случаях рекомендуется выбрать перестановку в виде t = cp (x), а затем выбрать J f (* p (x)) * (pr (x) dx = J f (t) dt Где t = (p (x)) Уравнение (1) может применяться справа налево.
Пример: 1) Найти Jе * 4) Найти J x • (x + 2) 100 dx. /♦ х 4-2 = т. Далее x = t-2, dx = eft. У нас есть: J x ‘(x + 2) 100 dx = J (t-2) t10Q dt = J t101 dt-2 J t100 dt = = lm (s-t-2) 102 2 (rr + 2) 101 ~~ 102 ‘101 + ~ 102 101 + 5) Найти ф. J ex + 1♦ указывает на экс = т. Далее x = Int, dx = y. так • ‘х л g dx _ g y g dt _ g dt » J ex + 1 7 т + 1 ~ J т (т + 1) ~ J dt (<+ *> = — В + C т 4 т + 1-в т т +1 -t = ln е * + 1 Здесь используется уравнение 16 базовой таблицы интеграции. ♦ Метод интеграции 3.Parts Пусть u = и u = функции с непрерывными производными. Далее d (uv) = u-dv + v-du.
Когда это равенство интегрировано, I d (uv) = J и dv + J vdu или J и dv = uv-J v du Полученное уравнение называется интегральным уравнением для каждой части. Вы можете свести интегральные вычисления J и dv к исходным вычислениям Jv du. Интегрирование по компонентам состоит в том, что подынтегральная функция данного интеграла выражается некоторым образом как произведение двух факторов и и dv (обычно это можно сделать несколькими способами сима). Затем, после нахождения v и du, в детали используется интегральная формула. В некоторых случаях это выражение может потребоваться использовать несколько раз. Вот некоторые типы интеграций, которые удобно вычислять методом частичной интеграции. t (t + 1) J t2 + t f dt T <* (* + §) -1 В
