Основные свойства проецирования

Основные свойства проецирования

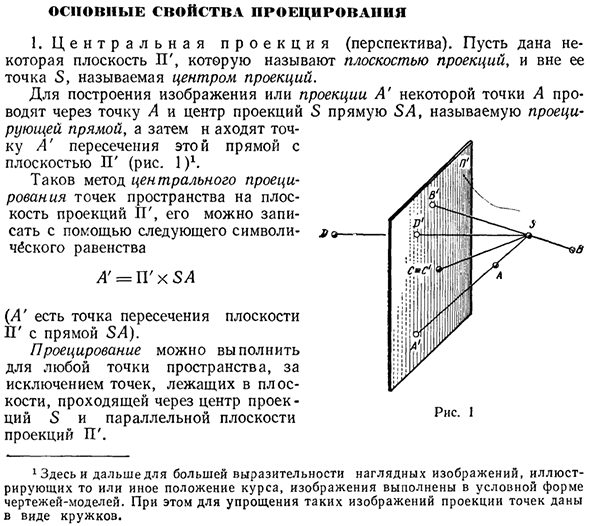
• Основные характеристики проекта 1. Центральная проекция (перспектива). Предположим, что плоскость IT, называемая плоскостью проекции, и точка S, называемая центром проекции, заданы вне ее. Чтобы создать изображение точки A или проекции A, проведите линию SA, называемую линией проекции, через центр точки A и проекции S и найдите точку A ‘на пересечении этой линии и плоскости IT (рисунок I) 1.

• Это центральная проекция пространственных точек на плоскость IT-проекции. Ее можно описать с помощью следующего символического уравнения. A = P’x 5L («Пересечение плоскости P и линии S / 1»). Проекция может быть выполнена в любой точке пространства, кроме точки, которая проходит через центр проекции S и лежит в плоскости, параллельной плоскости проекции GG.

Рисунок 1 1 и ниже, для повышения выразительности визуальных изображений, показывающих конкретное местоположение на курсе, изображения создаются с использованием модельных чертежей в традиционном формате. Людмила Фирмаль

Кроме того, для упрощения таких изображений точечные проекции приведены в форме кружков. На фиг.1 показана конфигурация проекции точек A, B, C и D в разных положениях относительно центра плоскости проекции P ‘и проекции S. Обычно проекции точек, которые проходят через центр проекции S и параллельны плоскости проекции P, рассматриваются как точка 1 на бесконечности плоскости P, потому что линия проекции этих точек параллельна плоскости проекции IP.

Будет сделано. Однако проекция для центра проекции 5 не может быть создана, поскольку линия проекции больше не определяется в одно и то же время, а проекция точки S на плоскость \ не определяется в одно и то же время. Проекция фигуры — это набор проекций всех ее точек. Тем не менее, не обязательно проектировать все его точки для построения проекции диаграммы.

Следовательно, проекция отрезка или прямой линии полностью определяется двухточечной проекцией. Проекция треугольника или плоскости определяется трехточечной проекцией. Проекция многогранника определяется проекцией его вершин. Поскольку зрительный процесс человека геометрически соответствует поведению центральной проекции, изображение объекта с использованием центральной проекции очень четкое (оптический центр хрусталика глаза считается центром проекции, а после сетчатки Стена почти считается проекционной плоскостью).

Центральная проекция слишком сложна и не сохраняет параллельность линий и пропорции сегментов, что сильно искажает первоначальную форму и размеры. Поэтому на практике мы часто используем параллельную проекцию, особенно ортографическую проекцию. Этот метод является частным случаем центральной проекции и обеспечивает более простую конструкцию изображения, когда центр проекции находится в точке бесконечности 5 <«и зависит от исходной формы и размера, как показано ниже Держит свойства.

2. Параллельная проекция. Предположим, что задана плоскость проекции GG и направление s проекции, не параллельное плоскости проекции. Если вы удалите центр проекции S в точку бесконечности, все линии проекции, которые пересекаются в точке бесконечности, будут параллельны определенному направлению s. Чтобы создать проекцию A ‘для любой точки A, нарисуйте проекцию через точку A Введение 1 бесконечных элементов (точек и линий) позволяет избежать геометрических локаций исключений, связанных с понятием параллелизма.

Таким образом, две прямые линии в одной плоскости всегда пересекаются в одной точке (нормальное или бесконечное расстояние). Две плоскости всегда пересекаются с прямой линией (обычно или бесконечно друг от друга). Найдите прямую линию, параллельную направлению проекции s и пересечению A ‘этой линии и плоскости GG (рис. 2).

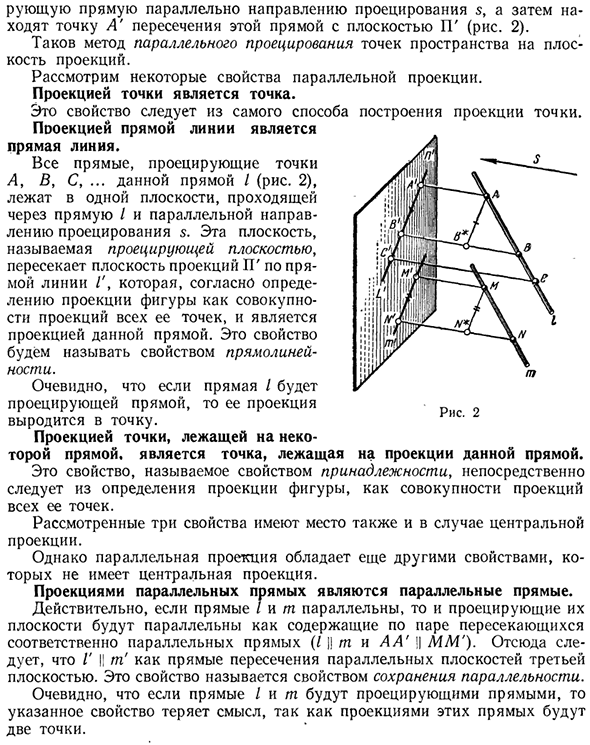
Это метод проецирования пространственных точек параллельно плоскости проекции. Рассмотрим некоторые характеристики параллельной проекции. Точечная проекция — это точка. Это свойство основано именно на том, как строится точечная проекция. Прямая проекция — это прямая линия. Все линии, проецирующие точки A, B, C, … для данной линии / (рис. 2), лежат в одной плоскости, которая проходит через линию / и параллельна направлению проекции s.

Эта плоскость, называемая плоскостью проекции, пересекает плоскость проекции P «прямой линией» Это проекция этой линии в целом на проекцию всех точек, согласно определению проекции фигуры. Это свойство называется свойством линейности. Очевидно, что если линия / является линией проекции, проекция будет сведена к точке. Точечная проекция на прямой является точкой на заданной прямой проекции.

Это свойство, называемое свойством принадлежности, следует непосредственно из определения проекции фигуры как набора. Проекция всех своих точек. Три рассматриваемые характеристики также относятся к центральной проекции. Однако параллельная проекция обладает другими свойствами, которых нет в центральной проекции.

Проекции параллельных линий — это параллельные линии. Фактически, если линии / и m параллельны, проецирующая их плоскость будет параллельна плоскости, содержащей пару пересекающихся параллельных линий (I \ m и A A ‘! | MM’). Отсюда следует, что GI! t ‘Как прямое пересечение параллельных плоскостей третьей плоскостью. Это свойство называется свойством сохранения параллелизма.

Очевидно, что если линия / и m являются проекционными линиями, это свойство теряет смысл, поскольку проекция этих линий составляет две точки. Доля проекции сегмента, параллельного или коллинеарного, равна пропорции самого сегмента. Пусть AB и MN будут отрезками на параллельных прямых I и mt и спроецированы на плоскость 1G (A’B ‘и M’N’) (рис. 2). На плоскости проекции нарисуйте отрезки A B * и MN *, параллельные отрезкам A’B ‘и M’N’ соответственно.

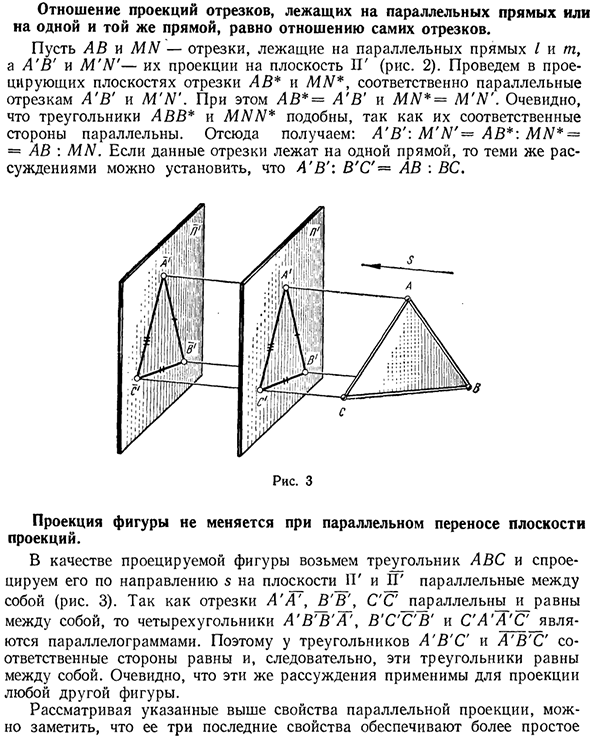
• Кроме того, AB * = A’B ‘и MN * = M’N’. Очевидно, что треугольники ABB * и MNN * похожи, потому что их стороны параллельны. Отсюда: A’B ‘: M’N’ = AB *: MN * — = AB: MN. Если эти сегменты находятся на одной линии, A’B ‘: BC’-AB: BC могут быть установлены с одним и тем же выводом. Рисунок 3 Проекция фигуры не меняется при перемещении плоскости проекции.

В качестве проекции возьмите треугольник ABC и спроецируйте его в направлении s плоскостиH ‘и P’ параллельно друг другу (рисунок 3). Сегменты A’A \ B’B ‘, CX’_parallel ^ и равны друг другу, поэтому прямоугольники A’VPZ’A’, B’C’C’B ‘и S’A’A’C’ являются параллельными сторонами сформироваться.

Таким образом, для треугольников A’B’C ‘и A’B’C’ соответствующие стороны равны и, следовательно, эти треугольники равны друг другу. Людмила Фирмаль

Очевидно, эти же соображения применимы и к другим проекциям фигуры. Учитывая вышеупомянутые свойства параллельной проекции, можно отметить, что последние три свойства обеспечивают более простую. Структура изображения с меньшим искажением исходной формы и размера по сравнению с центральной проекцией.

На самом деле трапециевидная параллельная проекция является трапециевидной, поскольку одно из свойств указывает на то, что параллельность линий сохраняется. Параллельная проекция параллелограмма — это параллелограмм, но в центральной проекции эти фигуры обычно проецируются на прямоугольник любой формы.

Следующие свойства имеют следующие отношения для проекции двух параллельных сегментов: A’B ‘: M’N’ = AB: MN. Откуда A’B ‘: AB = M’N’: MN (рис. 2), То есть в параллельной проекции искажение всех параллельных сегментов является постоянным. Отсюда, в частности, центр сегмента будет проецироваться на центр проекции сегмента. Последнее свойство можно использовать для переноса плоскости проекции параллельно самой себе.

Другими словами, вы можете отказаться от фиксации плоскости проекции. Кроме того, они говорят, что положение плоскости проекции может быть определено только с точностью до параллелизма. Эта ситуация настолько удобна, что широко используется для создания технических чертежей. 3. Ортогональная проекция.

Если направление проекции s перпендикулярно плоскости проекции IT, использование ортогональной проекции, особого случая параллельной проекции, упрощает настройку чертежа. В этом случае Нетрудно установить связь между естественной длиной сегмента и его длиной проекции.

Если отрезок AB образует угол a с плоскостью проекции, получим из A’B ‘(рис. 4) прямоугольный треугольник, нарисовав AB * || AB * B: AB * = AB, потому что или Ортогональная проекция чаще всего используется в технических чертежах, поскольку легче всего определить размер нарисованного объекта.

Рисунок 4 Описанный выше метод проекции может самостоятельно решать прямые задачи. Другими словами, вы можете создать проекцию из этого оригинала. Однако обратная задача воспроизведения (реконструкции) исходной задачи в соответствии с этой проекцией не решена четко.

Эту проблему можно рассматривать как проекцию любой точки на линии проекции, где каждая точка A «на плоскости проекции IT» проходит через A (рисунки 1, 2 и 4). Поэтому рассмотренные нами прогнозы не допускают первоначального решения и, как говорится, не имеют обратимого характера.

Чтобы получить обратимый чертеж, добавьте необходимые данные в чертеж проекции. Существуют различные способы сделать такие добавки. В этом курсе мы будем использовать только два типа обратимых рисунков: орфографические и сложные рисунки.

Смотрите также:

Предмет начертательная геометрия

Предмет и метод начертательное геометрии	Комплексный чертеж точки
Краткие сведения по истории развития начертательной геометрии	Комплексный чертеж прямой