Оглавление:





Параметрическое представление поверхности
- Параметрическое представление поверхности. Вернемся к проблеме аналитического выражения поверхностей в пространстве[ср. n°213], остановимся на-очень важном типе такого выражения, называемом параметрическим, — неизвестном читателю. В N°212 речь уже шла о
параметрическом представлении кривых в пространствесмотрите там(15) Таким образом, положение точки На ней определяется значением одного параметра и изменяется
с определенным интервалом. Например, при определении положения точки на Людмила Фирмаль
заданной поверхности по явному уравнению/(x, (2), мы уже имеем дело с двумя параметрами, роль которых заключается в определении положения точки на абсциссе-x и (X).) * ) Определение поверхностей с двумя параметрами, впервые введенное Эйлером, особенно широко и плодотворно использовалось в дифференциальной геометрии
Гауссом. Здесь функции CP, f, x определяются в нескольких областях (D) на»плоскости параметров» IU и являются смежными. Наш основной случай состоит в том, что каждая точка поверхности может быть получена только набором значений параметров, в результате чего p A b n e n I I(3)y s t A N A V l I V a u t обе стороны поверхности 295.
- Для о Тинга в ежах мы предполагаем, что и область(E), и поверхность связаны простым замкнутым контуром.(3) должны соответствовать друг другу в соответствии с формулой. Параметры I и V называются криволинейными координатами соответствующих точек. Для уравнения(3) зафиксировать значение одной из криволинейных координат, например, поставить-и^тогда, очевидно, получатся некоторые криволинейные уравнения -<Р(значения i0,■») «3′ =
ф(МО>=Х.(О Б), Которые все точки находятся на поверхности. Изменяя значение I0, мы получаем целое число C e m e y C t в такой » кривой (s)». Аналогично, если вы зафиксируете значение b=B0, вы также получите кривую на поверхности )0), макс=ф(Я,значения i0),х=х(я,^о х-г); Из такой «кривой (а)» она состоит из целого числа C e m e s t in o. все такие линии называются K o R d I n A tn y m I Li n I Pov e R x n o s t I. Если поверхность проста, то координатные линии из каждого семейства проходят через одну из ее точек. Все это уже хорошо известно читателям, но только на поверхности П Л О С для случая I
! [См. P°352.Предположим, что функция(3) не только непрерывна, но и имеет область (d) непрерывного частного дифференциала первой Людмила Фирмаль
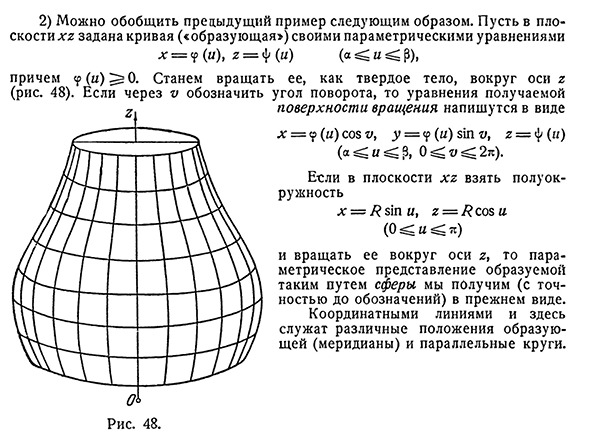
степени и рассматривает матрицу функций X » Y(4) №. с Пусть о значении параметра (I0, t1o) определяют точку 7io(XO, y,*0)поверхности, по крайней мере один из определителей квадратичной матрицы(4) отличается от нуля. Четырнадцать ^о. Далее перепишем первые два уравнения(3) в виде»=Ф («) (А<я<р),<р(я) Х>0. Повернем его, как твердое тело, вокруг оси g(рис. 48). Полученное уравнение при отображении угла поворота через V Райс, 48. Это
плоскости вращения записано в виде х=с? (Я)сөз я,у=СР (я)ЗШ я,2=ф(я)(а^.И^9,0■u2ts). Если взять полукруг x=T в плоскости HCG?8Ш», 2=/? Соз а (о и ТС) и параметрическое представление сферы, сформированное таким образом, вращая ее вокруг оси 2, мы пилучим (вплоть до обозначения) в том же виде. Координатными линиями здесь являются различные положения окружности, параллельной шине (Меридиану).
Смотрите также:
Решение задач по математическому анализу
| Замена переменных в двойных интегралах | Сторона поверхности |
| Аналогия с простым интегралом. Интеграл по ориентированной области | Ориентация поверхности и выбор ее стороны |
