Оглавление:









Переход через скорость звука. Предельные линии. Примеры точных решений
Переход через скорость звука. Предельные линии. Примеры точных решений. Представим себе несжимаемую жидкость, обтекающую с определённой по величине и направлению скоростью на бесконечности, замкнутый контур.
Если, не меняя направление скорости, мы увеличим величину её, то конфигурация линий тока останется неизменной — только нумерация функций тока изменится. Существует лишь одно семейство кривых, которые могут служить линиями тока при обтекании (под данным углом атаки) заданного контура несжимаемой жидкостью. Совсем иначе будет обстоять дело в сжимаемой жидкости.
Смотрите также:
Если в несжимаемой жидкости мы могли написать где так что для мы имели просто уравнение Лапласа, то в сжимаемой жидкости мы должны положить так что уравнение будет содержать в качестве коэффициента число Маха на бесконечности.
Сама конфигурация линии тока будет меняться с изменением числа Маха и, таким образом, причём одному профилю будет отвечать бесконечное множество линий тока, представляющих обтекание этого профиля при различных по величине скоростях на бесконечности.
Смотрите также:
Несжимаемая жидкость получается как предельный случай, когда, так что в выражении для можно пренебречь членом, содержащим; это приводит к приближённому условию. Другой предельный случай получится, если скорость будет сверхзвуковой и.
Особенно резко проявляется изменение формы линий тока, когда в плоскости течения (обладающего ещё дозвуковой скоростью на бесконечности) возникают сверхзвуковые зоны. Людмила Фирмаль
- Мы уже видели в одном из предыдущих параграфов, на примере обтекания контура, близкого к кругу, что уже при на профиле появляется точка, где при дальнейшем росте скоростей следует ожидать появления сверхзвуковой области.
Но здесь возникает новая специфическая трудность. Дело в том, что течения сжимаемой жидкости обладают двумя особенностями по сравнению с движениями жидкости несжимаемой. Во-первых, в сжимаемой жидкости невозможны бесконечно большие скорости (максимальная возможная скорость есть во-вторых, в сверхзвуковом потоке газа, в противоположность жидкости несжимаемой, трубки тока расширяются с увеличением скорости (см. § 8).
Последнее обстоятельство приводит к тому, что в сверхзвуковой зоне линии тока будут, расширяясь, расходиться по отношению к обтекаемой границе; в дозвуковой зоне, напротив, линии тока будут сужаться и как бы сходиться с приближением к сверхзвуковой зоне. Можно ожидать, что при заданном контуре будут существовать скорости на бесконечности, при которых невозможно будет удовлетворить этим обоим законам.
Смотрите также:
Конечность скорости, с другой стороны, приводит к тому, что там, где решение для несжимаемой жидкости даёт бесконечные скорости, например, при обтекании острия, там решение для жидкости сжимаемой либо не существует, либо соответствующие линии тока не образуют острого угла. Математически дело сводится к тому, что в сверхзвуковой зоне могут появиться точки и целые линии, на которых производные от скоростей будут обращаться в бесконечность.
Это так называемые «предельные линии». Такие решения уравнений газовой динамики, формально существующие, физического смысла не имеют и реализоваться не могут. В этих случаях движение перестраивается так, что возникает линия сильного разрыва (не совпадающая, конечно, с предельной линией), и решение с самого начала следует искать мы получим, пренебрегая членом, содержащим очень большой.
Если В этом последнем случае, так как по (9.22) Таким образом, в этом предельном случае поток вновь не зависит от числа Маха на бесконечности. Не в виде непрерывного безвихревого обтекания, а в виде движения, в котором имеется поверхность разрыва, форма и местоположение которой заранее неизвестны и после перехода через которую течение становится вихревым.
Опыт показывает, что скачки, как правило, «садятся» на крыло в сверхзвуковой зоне (крыло движется с дозвуковой скоростью). Такие же скачки образуются в сопле Лаваля, даже при нужном перпаде давления, сразу после того, как совершился переход через звуковую скорость, если только профиль сопла не удовлетворяет специальным условиям (см. следующий параграф).
Условие наличия предельных линий в том или ином решении уравнений газовой динамики, т. е. Условие, при котором появляются бесконечные ускорения (производные от скоростей), нетрудно написать. В самом деле, это условие очевидно равносильно обращению в нуль якобиана; по последний можно записать так: что вследствие (16.8), (16.9) и (16.10) даст.
Мы видим, что если, наш определитель не может обратиться в 0; значит, предельные линии невозможны в дозвуковом потоке. Предельные линии образуются там, где Любопытно, что первые примеры точных решений, в которых осуществлялся переход через скорость звука, обладали все предельными линиями. Татаренчик первый показал, как можно найти ряд точных частных решений уравнений газовой динамики, в которых осуществляется переход через скорость звука, причем движения имеют физический смысл (предельная линия не успевает образоваться).
Чтобы получить примеры таких решений, вернёмся к уравнениям Чаплыгина и обратим внимание на то, что каждый член ряда (стр. 118) будет формально удовлетворять уравнениям газовой динамики. Татаренчик рассматривает решения вида: (19.2) где А и В — постоянные, а zn по-прежнему будет и удовлетворяет уравнению гипергеометрического ряда (16.16) : Здесь n — любое число.
Вместе с Татаренчиком положим: тогда для получим: Это уравнение интегрируется и даёт. Итак, мы можем принять в качестве решения: При этом для получается (см., например, (16.21)]: Рассмотрим частные случаи. Положим сперва тогда будет. Найдём сперва, как выглядят в плоскости линии.
Так как вдоль этих линий и так как, по (16.7) и по (19.5) Интегрируя по пределах от до получим: отсюда Остается найти лишь. Это суть значения, которые принимают х и у в функциях от v на линии. Но вдоль линии, будет причём. Таким образом, линия в плоскости переходит в прямую, параллельную оси Ох, и можно считать что же касается х0, то оно найдётся квадратурой.
Таким образом, линиями будет семейство кругов с центрами вдоль оси Ох и различных радиусов (см. Рис. 48, на котором изображена «верхняя» часть течения). Так как на линии у = 0 будет — все линии тока под прямым углом пересекают ось Ох. Рассмотрим линию тока. По (19.5) там, где эта линия тока пересекает ось Ох, будет. Перемещаясь вдоль линии тока, мы будем встречать различные значения v.
Значит, на всех тех линиях тока, для которых скорость v на оси Ох будет меньше, чем бесконечные ускорения не возникают, и соответствующие течения имеют физический смысл. На рис. 48 изображены эти линии тока, вплоть до крайней возможной.
Круги постоянной скорости сгущаются по мере приближения к линиям тока, на которых возможны бесконечные ускорения. Людмила Фирмаль
- На рис. 49 изображена одна из таких линий тока и нарисованы характеристики первого и второго семейства, которые возникают в нашем движении в сверхзвуковой зоне. Второй частный случай решения (19.3), (19.4) получим, полагая тогда Вдоль линии Так что можно написать: где— значения х и у в тех точках. Как и в предыдущем примере, определим х0 и у0, перемещаясь по линии.
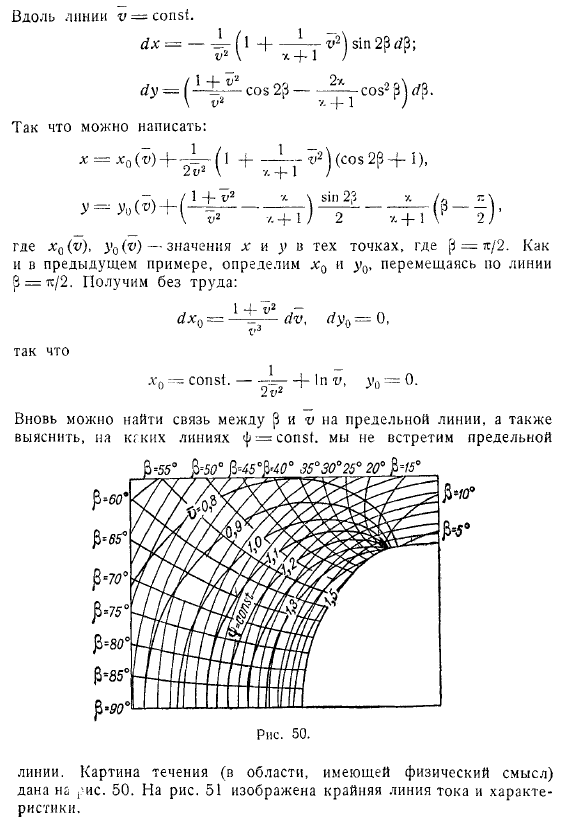
Получим без труда: так что Вновь можно найти связь между и на предельной линии, а также выяснить, на каких линиях, мы не встретим предельной линии. Картина течения (в области, имеющей физический смысл) дана на рис. 50. На рис. 51 изображена крайняя линия тока и характеристики. Другие примеры точных решений для движений с до- и сверхзвуковыми скоростями можем найти в статье Ринглеба и Крафта и Диббла.
Эти авторы отправляются также от решений Чаплыгина. Полезно отметить, что решения вида (19. 2) переходят в несжимаемой жидкости в решения типа где В самом деле, для несжимаемой жидкости мы имели бы вместо (19.2) просто (см. стр. 119) : Но тогда Отсюда и получится (19.6). Так решениям Татаренчика отвечает.
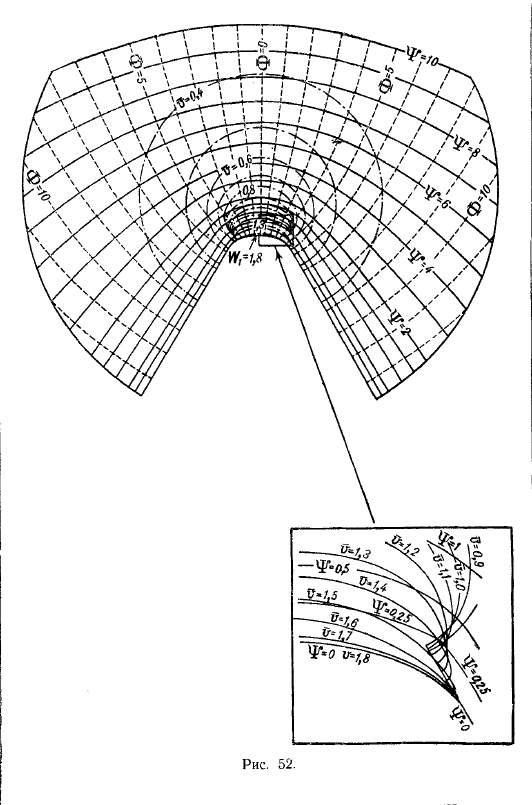
Здесь линии тока — семейство парабол с общей осью — осью Ох, а линии равных скоростей суть концентрические окружности (с центром в начале). На рис. 50 видно, как искажаются эти линии из-за сжимаемости. Крафт и Диббл рассмотрели детально случаи, когда. На рисунке 52 изображены некоторые линии тока и линии v = const, для случая.
Отдельно показано в увеличенном виде поле, обведённое квадратом. Здесь как раз появляются предельные точки. Лишь вне некоторой линии тока возможно физически осуществимое обтекание, сходное с тем, что разобрал Татаренчик. В несжимаемой жидкости этому движению отвечает обтекание угла в 60о.
В приведённых примерах вопрос о возникновении или невозникновении предельных линий решается задним числом — после того, как решение получено, применяется критерий (19.1). Нельзя ли, однако, выяснить заранее, получатся ли безразрывные, имеющие физический смысл, решения при обтекании данного контура, при данной скорости на бесконечности и при условии возникновения сверхзвуковой зоны.
Этот вопрос тем более важен, что очень редко удаётся получить точное решение задачи обтекания. Почти всегда приходится довольствоваться решением приближённым, а благодаря неточности того или иного приближённого метода мы можем пропустить появление опасных областей.
