Оглавление:




Понятие группы. Некоторые свойства групп
- Концепция группы Некоторые свойства группы. текст Определите следующие определения: Закон определения 1. Позиция Т называется группой G. Если этот закон имеет значение, Существует нейтральный элемент е относительно закона Т, для каждого Существуют обратные элементы от a до * элемента a из A, то есть элементы от aTa до x-e При использовании мультипликативных записей песен.
- Для элементов определение 1 может иметь следующий формат: Определение 2. Набор A элементов a, b, c, … Определяется законом синтеза, называемым умножением и конфигурацией Соответствие каждой паре элементов a и b множества A определено Элемент c = ab в этом множестве называется группой G. Закон отвечает следующим требованиям: 1 °) a (bc) = (ab) c (связывание).
2 °) есть элемент е множества А. Людмила Фирмаль
Этот набор элементов ae = a (наличие нейтрального элемента Гаишник). 3 °) Элемент А в множестве А имеет обратный элемент Напишите ~ 1 так, чтобы ~ 1 = e. Нейтральный элемент e обычно называется группой группы G. Синтетический закон T, действующий в группе G является ком- Если коммутативно, группа G называется коммутативной или абелевой.
Аддитивные обозначения часто используются для абелевых групп. Элементный состав. В этом случае нейтральным элементом является абель Группа называется ноль. Рассмотрим групповой пример. 1) Множество Z целых чисел образует абелеву группу относительно Добавлен. На самом деле, добавление целого числа Бой это явно закон состава.
Понятно, что этот закон ассоциативный Взаимозаменяемы с венами. Нейтральный элемент (ноль) является целым Ноль. Инверсия целого числа а является целым числом Номер -a. 2) Набор положительных действительных чисел образует абель У группы по умножению. Эта операция Закон композиции.
Очевидно, этот закон является ассоциативным и коммутативным. Тибан. Нейтральный элемент — это действительное число 1. Инверсия числа a> 0 — это число 1 / a. 3) Линейное пространство образует относительные абелевы группы Но добавление элементов. Эта операция является законной. Конфигурация. Согласно аксиоме линейного пространства этот закон Ассоциация и коммутация.
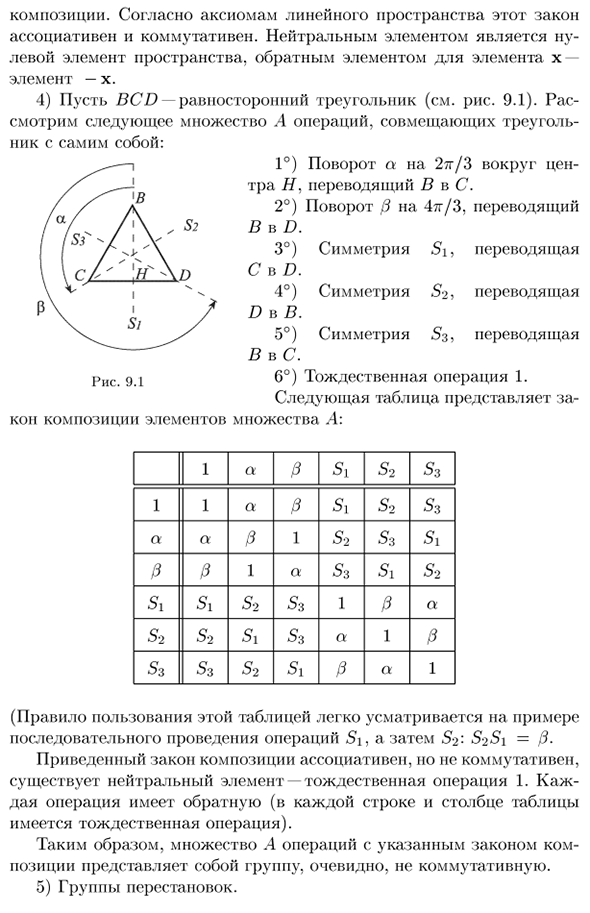
Нейтральный элемент Левый космический элемент, обратный элементу x, Элемент х. 4) Сделайте BCD равносторонним треугольником (см. Рисунок 9.1). Лас — Давайте посмотрим на следующий набор операций A, который объединяет треугольники. Ник с собой: 1 °) 2TG / 3 вращения вокруг цены Перевод с Tra H, B на C. 2 °) Поворот /? Перевод 4тг / 3 В D 3 °) Си симметрия, перевод С на D 4 °)
- Симметричный перевод S2 B D 5 °) Симметричный перевод S3 В С 6 °) Та же операция 1. Следующая таблица рисовый Кон конфигурация элементов в наборе А: 1 но р си 52 53 1 1 но P си 52 53 но но 1 52 си 52 P 1 но 53 53 си си си 52 53 1 но P 52 52 53 си P 1 но 53 53 си 52 но P 1 (Правила, которые используют эту таблицу, легко увидеть в примерах. Последовательная операция Si, затем S2: S2S1 = / 3. Вышеуказанный закон композиции является ассоциативным, но не коммутативным.
Есть нейтральный элемент — та же самая операция. Каждая операция противоположна (в каждой строке и столбце таблицы) Там же операция). Следовательно, множество A операций с указанным ком законом A Позиция является группой и явно не взаимозаменяемы. 5) Группы перестановок.
Отображение 1-в-1 / произвольный набор E Называется перестановка множества E. Людмила Фирмаль
Элемент a множества ходит пересекает элемент / (a) и наоборот New / ~ 1 преобразует / (a) в a. Перестановка f (a) = a является Имя в наборе называется перестановкой идентификаторов. Перестановка, если множество состоит из элементов a, b, c, … ku / Этот набор записывается как: (А б f (a) f (b) f (c) ..
Множество P перестановок множества E естественным образом Закон состава определяется: если D и f2 являются перестановками E, Последовательный D & D этих перестановок Сразитесь с некоторыми перестановками множества Е. COM- Позиция ассоциативная. Если набор содержит замену идентичности, обратная Перестановка для каждой перестановки / и Две перестановки D, D, состав D, D и ясно P Представляет группу.
Все перестановки множества E образуют группу. Последний из Эта группа из n элементов из называется симметрией Группа Сн. Давайте посмотрим на пример 4). В этом примере была рассмотрена операция. Объедините равносторонний треугольник BCD с собой. о E = означает множество вершин этого треугольника: E = (BCD).
Очевидно, что группа операций, рассмотренная в примере 4) Перейти к следующей группе Электронная перестановка: а = s2 = 6) Рассмотрим группу Z2, состоящую из двух элементов 0 и 1 Какое умножение определяется по правилу: 0-0 = 0, 0-1 = 1, 1-0 = 1, 1-1 = 0. (9.1) Единицей группы является элемент 0. Эта группа называется группой, остаток которой по модулю 2.
7) Рассмотрим группу из двух элементов. 1) личность Фактическое преобразование евклидова пространства (представляя это Полицейский 0); 2) Отражение евклидова пространства от начала Координаты (указывает на этот элемент 1). Очевидно, умножение (т.е. последовательная операция) Элементы 0 и 1 1) и 2)) выполняются в соответствии с правилом (9.1).
Смотреть Проблемная группа отличается только от группы Z ^ (пример 6) Природа элемента. Эти две группы имеют одинаковые групповые свойства. Обратите внимание на следующие свойства группы (используйте Типичная форма композиции). Теорема 9.1. Для aoG1-e от a до ha-e. Доказательство. х является обратной величиной элемента -, -1. Это хх = е.
Тогда a = ae = a (a rx) = (aa 1) x = ежик, то есть a = ежик. Исследователи Но a-ha-a (еж) = (a ~ 1e) x = a ~ xx-e, то есть ea = a. теорема Проверенная. Теорема 9.2. Отношение к элементу группы А Я ношу еа = а. Доказательство. В теореме 9.1, а = в дополнение к ней aoG1-е. Следовательно, ea = (aa˜1) a = a (a˜1a) = a, то есть ea = a. Теорема доказана. Теорема 9.3. Если ax = e и ay = e, x = y.
Доказательство. Поскольку ay = e, y является обратным элементом а и, следовательно, согласно теореме 9.1, у а = е. Кроме того, у = -уе-у (ах) = (з / а) w = ежик = w. Теорема доказана. Из доказанной теоремы получены следующие важные результаты. Система 1. Обратный элемент элемента a Элемент а. Или же элементы a-1 оба левые и правые Обратный элемент элемента a (т.е. aa ~ 1 = e и a ~ 1a = = е).
Следствие 2. Один в любой группе уравнений ax = b и ya = b Решить нарочно. Решения этих уравнений являются соответствующими На практике элементы x = a до xb и y = ba до x. Следствие 3. Группа имеет один нейтральный элемент. мент (единица группы) (e = e * для ae-a и ae *). Замечания. Обратный элемент (ab) к r Элементом ab является b ~ 1a ~ 1. На самом деле, используя ассоциативное свойство умножения, (Ab) (b-1a-1) = a (b-1) a-1 = aea-x-aa-x-e.
Смотрите также:
| Тензор момента инерции | Изоморфизм групп. Подгруппы |
| Законы композиции | Смежные классы. Нормальные делители |
