Поверхности

Поверхности

• поверхность Функция двух независимых переменных, заданных уравнением х = е (х, у). (1) Переменные x и y> z рассматриваются как координаты точки. Возьмите точку M на плоскости xOy. То есть пары x и y (его координаты). Согласно уравнению (1) пара x и y соответствует определенному z. Следовательно, можно сказать, что уравнение (1) связывает точку M (x, y) в плоскости xOy с точкой P (x, y, z) в пространстве. Изменение положения точки M в плоскости xOy дает другую точку P (x, y> z).

. Например, рассмотрим формулу, которая выражает расстояние между двумя точками (§2 формула (*)): I PA I = V ^ x-xJ + (yt-yX + (r, — *,) 1. Предположим, что точка P1 фиксирована, а расстояние между точками P и P2 является постоянным и равным. И точка P1 может двигаться.

Геометрическое положение точки P (x, yy z), координаты которой удовлетворяют уравнению (1), называется поверхностью Людмила Фирмаль

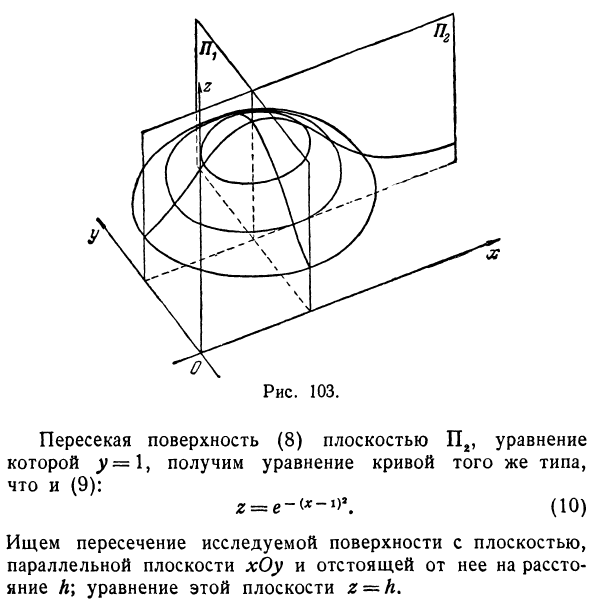
В этом случае геометрическое положение точки Pr является поверхностью шара или, другими словами, сферой. Координаты точки Px представлены a, b> c, а координаты Pt представлены x, y, z (где x, y, z — переменные). Уравнение (*) затем можно переписать в виде R = V (х-а) * + (у-б) * + (г-кр или Рисунок 103. Уравнение по поверхности (8) плоскостью Пг Это y = 1, и вы получите уравнение кривой того же типа, что и (9). z = e — (* — i) \ (10) Мы ищем пересечение исследуемой поверхности и плоскости, параллельной плоскости xOy. На расстоянии h \ от этой плоскости уравнение этой плоскости равно z ~ h.

Подстановка z = h в уравнение (8) дает: Прологаритизм по обе стороны последнего равенства и трансформации. У нас есть: (LH-1) «-h или — 1)» — в A, (* -1) H-0′-1), = 1n |. (11) Это круговое уравнение с радиусом j / ^ ln-, центрированное в точке (1, 1, A). Чтобы радиус был действительным, положительное число должно быть под знаком квадратного корня.

• И поскольку логарифм является положительным по отношению к числовому значению и единице, -r> 1 или h <1. Это означает, что вы рассмотрели Точка пересечения пересекает плоскость z-h, только если 0 <Λ <1. Если h = 1, радиус исчезает. Другими словами, круг сжимается до точки. Следовательно, поверхность, определяемая уравнением (8), образована из круга (11), вытянутого вокруг кривых (9) и (10). Окружность, образующая поверхность, увеличивается с уменьшением h>, то есть по мере приближения к координатной плоскости xOy.

Это неявная функция. Поэтому уравнение () называется уравнением сферы с центром в точке (a, b> c) и радиусом, равным R. Таким образом, уравнение (1) определяет поверхность и называется уравнением поверхности. Используйте метод сечения, чтобы найти тип поверхности, определенный уравнением (1). Это продемонстрировано на примере.

Координаты, удовлетворяющие уравнению (), определяют точку на сфере. Людмила Фирмаль

Пример 1. Найти форму поверхности, заданную формулой. ax + by + cz + d = ~ 0, (2) Другими словами, найдите геометрический смысл неявной функции, определенной в уравнении (2). Для этого сначала найдите пересечение поверхности и оси Oz. Поскольку абсцисса и ордината точки на оси Oz равны нулю, целевая точка удовлетворяет этим условиям и уравнению (2). Подставляя в уравнение (2) x = 0, j / = 0, z = — Итак, точка C ^ 0, 0 — это точка Пересечение поверхности и оси Oz определяется уравнением (2).

Чтобы найти пересечение поверхности и оси Ox, введите уравнение (2) y и 2 = 0. Отсюда х = — ~. Таким образом, точки A ^ — ~, 0,0 ^ являются пересечением поверхности и оси Ox. Аналогично, предполагая, что x = 0 и 2 = 0 в уравнении (2), вы можете видеть, что точка B ^ 0 является пересечением поверхности (2) и оси Oy (рис. 101). Давайте посмотрим, что происходит, когда поверхность (2) пересекает плоскость xOz. Поскольку уравнение для этой плоскости = = 0, при условии y-0 в уравнении (2), ax + cz -M = 0. (3) Как указано в разделе. II, все уравнения 101.

Две первые степени Уравнение (3) определяет прямую линию в плоскости xOz, потому что неизвестное определяет прямую линию на плоскости. Линия, определяемая уравнением (3), проходит через точки A и C, поскольку координаты удовлетворяют уравнению (3). Проверьте это для пункта А.Предполагая l: -0 в уравнении (2), находим пересечение поверхности и координатной плоскости yOz. Опять же, получить линию, определяемую уравнением на + cz + d = 0, (4) Пройдите через точки B и C Наконец, пересечь поверхность (2) с плоскостью xOy.

То есть, если вы установите z = 0 в уравнении (2): ax + by + d = 0. (5) Уравнение (5) находится в плоскости xOy и определяет прямую через точки A и B. Следовательно, поверхность, определяемая уравнением (2), пересекает координатную плоскость вдоль треугольника ABC. Пересечь плоскость, параллельную плоскости xOy, чтобы найти окончательный вид поверхности. Эта плоскость принимает уравнение r = z-h в уравнении (2) ax + by + ch + d = 0. (6) Это линейное уравнение в плоскости z — h. Найдите пересечение yOz \ plane и прямой (6) для этого Положите в уравнение (6): a: = 0, y == — ch to rd ^ ^ ay Точка 0, -ch + d ^ ^ также находится на линии BC9. ч + д.

Чтобы удовлетворить его ординату — ^ — и применить ч Формула (4). Если вы установите >> = 0 в уравнении (6), вы найдете пересечение координатной плоскости и линии (6) xOz; в этом все дело. Есть точка Е,На линии AC, потому что координаты удовлетворяют уравнению (3). Поскольку число h может быть изменено, исследование показывает, что поверхность, определенная уравнением (2), образована прямой линией K%, которая скользит вдоль прямой, где пересекаются AC и CB. Эта поверхность плоская. Таким образом, линейное уравнение с тремя неизвестными в пространстве определяет плоскость.

Пример 2. Найти тип поверхности, определяемый уравнением Скрестите лицо с плоскостью xOz9. Это значит x2 Уравнение (7) дает ^ = 0. z = –2, это параболическое уравнение в координатной плоскости xOz (рис. 102). (Искусство) * (бВч) z Рисунок 102. Пересечь поверхность с плоскостью yOz, т.е. заданной уравнениями and2 (7) х = 0, получается следующая формула Это параболическое уравнение (см. Главу 3). Найти пересечение исследуемой поверхности с плоскостью z = h, то есть параллельно плоскости xOy и на расстоянии h оттуда. Поставить Z-H сверло и 2 (7), ч- или = — = 1. Y ‘ == т + (А В ч) 2 (б В ч) 2

Это уравнение для эллипса с полуосью al ^ h и b] / «ft. Чем больше h, тем больше полуось эллипса. Следовательно, эллипс проходит на расстоянии xOy от координатной плоскости. O В случае h = 0 полуось равна нулю. Таким образом, исследуемая поверхность образована эллипсом в плоскости, параллельной плоскости z = 0t.х * у * Парабола Z = -T и Z ~ ^ этой поверхности Это называется эллиптический параболоид. Пример 3. Изучите форму поверхности, заданную уравнением Найдите пересечение с плоскостью Пж. Уравнение равно n: -1 (рисунок 103). При присвоении уравнению (8) * = 1 принимает следующий вид: gsse-to-D \ (9) Эта кривая была исследована гл. VIII, §5, пр. 3; Он лежит в плоскости, параллельной плоскости yOz, и на расстоянии 1 оттуда.

Смотрите также:

Предмет высшая математика

Координаты в пространстве	Линии уровня
Некоторые простые уравнения	Частные производные