Оглавление:


Предельное состояние закрученного стержня из идеально-пластического материала
- Предельное состояние скрученного стержня выполнено из идеального пластического материала. Если стержень изготовлен из идеального пластика, то в предельном состоянии аффикс находится- Рис 133. Отклонения во всех точках поперечного сечения равны по величине и изменяются только в направлении.
Рассмотрим две бесконечно близкие орбиты касательных напряжений фигуры G и G’: 133. Когда замкнутый объем был разрезан между двумя цилиндрами у основания G и G ’ от стержня и сформирован параллельно оси стержня, тонкий замкнутый профиль (90.1) без напряжения на стороне был получен только статическим состоянием, поэтому это верно как в упругом состоянии, так и в пластичности.
Мы применяем его к рассматриваемым тонкостенным стержням; понимая расстояние между линиями G и G’b, мы получаем.: Людмила Фирмаль
И так оно и есть. БТТ=Конст. б=Конст. Поэтому траектория тангенциального напряжения в критическом состоянии стержня, изготовленного из идеального пластического материала, является равноудаленной кривой. Чтобы построить их, нужно отправить из контура. Мы строим группу линий, перпендикулярных контуру,
размещая на этих линиях равные длины отрезков, начиная с точек контура. Соедините концы этих сегментов, чтобы получить предельное состояние [94]скрученного стержня 205 Касательная траектория напряжения. Для круга, например, траектория касательного напряжения является концентрической окружностью
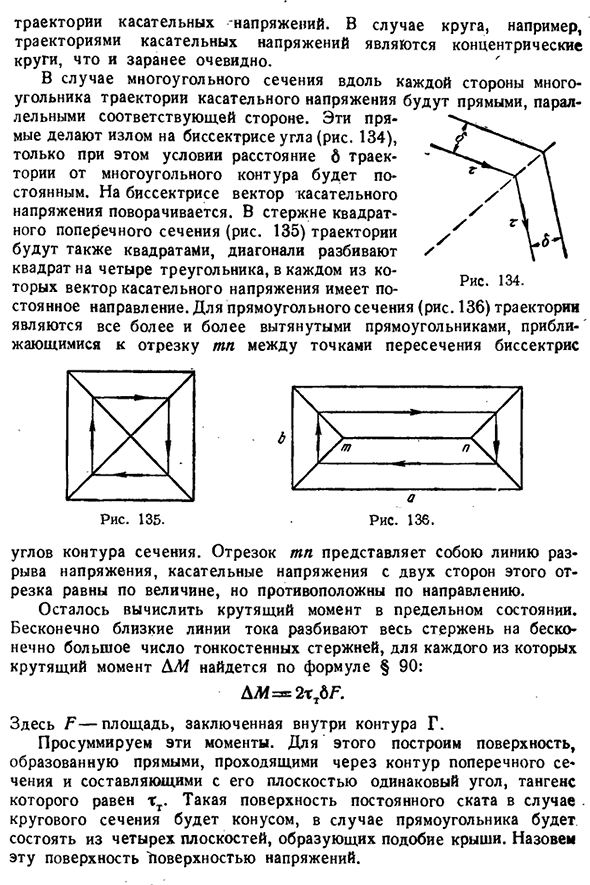
- и презентабельна. Для полигонального сечения вдоль каждой стороны полигона локус касательного напряжения представляет собой прямую линию, параллельную соответствующей стороне. Эти прямые линии делают разрыв на биссектрисе угла (рис. 134), только при этом условии расстояние траектории от контура полигона будет постоянным. В биссектрисе вектор касательных напряжений вращается. Стержень квадратного сечения (рис. 135) траектория также является квадратом, диагонали делят квадрат на четыре треугольника, в каждом из которых вектор касательных напряжений имеет определенное направление.
Для прямоугольных сечений (рис. 136) орбита представляет собой более вытянутый прямоугольник, приближающийся к отрезку TP между пересечением биссектрисы Рис, 136. Угол наклона контура сечения. Отрезок TP представляет собой линию разрыва напряжений, касательные напряжения на обеих сторонах этого отрезка равны по величине, но противоположны по направлению. Осталось рассчитать крутящий момент предельного состояния. Токовая линия замыкается бесконечно, для каждого по крутящему моменту, ломается весь стержень до бесконечности числом тонкостенных стержней! Найдено по формуле§ 90:
где F-площадь, заключенная в контур G. Давайте подытожим эти моменты. Людмила Фирмаль
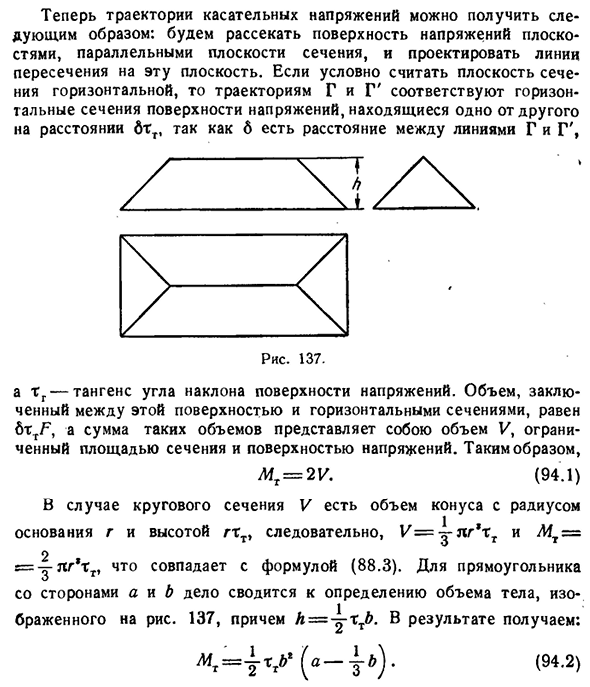
Для этого мы строим поверхность, образованную прямой линией, которая проходит через контур поперечного сечения и составляет такой же угол с плоскостью, касательная которой равна TT. Поверхность определенного склона в случае такого круглого сечения представляет собой конус, а в случае прямоугольника она состоит из четырех плоскостей, образующих подобие крыши. Назовем эту поверхность поверхностью напряжения.206 кручение(Глава VII Траекторию касательного напряжения можно получить следующим образом: рассечь поверхность напряжения плоскостью, параллельной плоскости поперечного сечения, и спроектировать точки пересечения на этой плоскости.
Если принять плоскость горизонтального сечения, то она соответствует горизонтальному сечению орбитальной поверхности G и G’Stress, расположенной с одной стороны от другой на расстоянии ytt, так как 6 линий G и G’between, t g-касательная наклона плоскости напряжений. Объем, заключенный между этой поверхностью и горизонтальным сечением, равен 6ttF, сумма таких объемов равна объему V, ограниченному площадью поперечного сечения и поверхностью напряжения. Итак, M T=2U(94.1).) В случае круглого поперечного сечения V имеется объем конуса с базовым радиусом g и высотой GTT, при этом V=^n r * x T и L4T=2 =Y LG*TT, что соответствует формуле (88.3). В случае прямоугольника со сторонами a и B вы будете определять объем тела, показанного на рисунке. 137,и L=U т ты. Результаты таковы:
Смотрите также:
| Кручение упругих стержней сплошного профиля | Основные определения |
| Опытное исследование кручения | Общие теоремы о моментах |
