Оглавление:

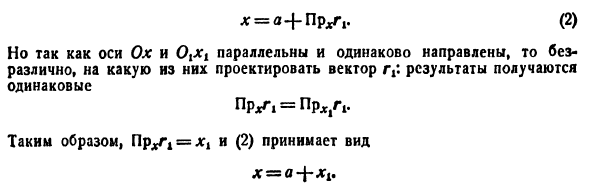






Преобразование координат
- Преобразование координат n ° 1.Ответ о себе. Параллельная система передачи. также Поскольку вы определяете пространственную линию (или поверхность) в одной системе координат, например, в аналитической геометрии на плоскости, вам может потребоваться определить пространственную линию в другой системе координат. Чтобы решить эту проблему, вам необходимо выяснить, как координаты одной и той же точки выражаются в двух системах координат.
Пусть это будет точка Af, у Ohug есть координаты (x, y, r) в первой («старой *») системе координат, а система координат OjJW (xlt yt, r,) во второй (. * *) вы. Представляем старый и новый радиус-векторы для точки М. OM = R, B ^ M = R4. Между векторами концертов очень простая связь. Другими словами, _ легко увидеть (Рисунок 319) Это (1) r = u + r4. Следовательно, старый радиус-вектор точки равен новому радиус-вектору, добавленному к (старому) радиус-вектору новой начальной точки.
Как известно, координаты точки M являются проекциями этих радиус-векторов на соответствующие оси системы. x = Pr ^ r, xx = Pr „r .. Людмила Фирмаль
Обратите внимание, что если новая ось 0 ^ xi 0% yi Ofii параллельна (и в том же направлении) старой оси, то есть, если новая система координат получена из старой системы координат с использованием параллельного переноса, Рассмотрим простой случай. В этом случае положение новой системы полностью определяется путем установки новой начальной точки O. Пусть (a, b, c) будет (old1) новой координатой начальной точки Oh. Вычислите уравнение (1) на ось Ox. PrLg = PrL001 + PrLg1. Рисунок 319.
х = Q + прибл (2) Однако, поскольку оси Ox и Oghl параллельны и направлены в одном и том же направлении, нет никакой разницы в проецировании на вектор / y. Результат тот же Pr * r 1 = PrL | r 4. Следовательно, Prxri = xk и (2) принимают следующий вид: Ситуация аналогична другим координатам М. Таким образом, z = c + z „ То есть при параллельной передаче системы координат старые координаты точки равны новым координатам и добавляются к старым координатам нового начала координат. п * 2. Система вращения.
- Более сложный случай, когда новая система с общим началом со старой системой берется из нее с помощью некоторого вращения. Положение каждой из трех новых осей определяется путем установки угла, который образуется со старой осью. В следующей таблице показан угол, образованный каждой старой осью и каждой осью Гобли. Ах | Ах | Ог Ojc, «я Пи 7i Qy, «1 фк Оз, «1 стр. 7i Поскольку обе системы имеют общее происхождение, точка M имеет одинаковый радиус-вектор r в обеих системах.
Когда единичный вектор новой оси обозначен / Jit ku, согласно основному уравнению векторной теории » LA + lL + gJ- Спроецируйте это уравнение на ось Ox. Учитывая таблицу углов выше, x = xt cos a, — \ — yk cos ctt + z, cos a ,. Поскольку это же уравнение применимо к координатам y и r, x = xx cos при cos <xY Zj cos cta y = xt cos P, cos h + Zj cos z = xx cos y, + yt cos + Zj cos
cos * otj -f- cos» p, + cos «7t = 1, cos» Ct, + COS1 P, -f «COS1 7, = 1 , Cos a, cos a, -f-cos p, cos ps -f-cos 7t cos 7, = 0, (5) COS as cos, COS Pj COS P, -j «COS COS 7 = 0, cos o cos cos cos p4 cos p, 4-cos 7, cos ft = 0. Первое из этих соотношений связывает вектор / | направляющие косинусы.
Полезно отметить, что существует связь между письменными косинусами cos8 «j -f- cos * p, + cos * h = I, Людмила Фирмаль
Второе и третье отношения имеют одинаковое значение. Четвертое — это только условие взаимной перпендикулярности между единичными векторами it и Jx.Пятый и шестой отношения также установлены. Изменение роли системы Ohug и Ohhukh19 дает шесть других взаимосвязей вместо того, чтобы соединять один и тот же косинус (5).
Например, косинус направления вектора I В новой системе они связаны по формуле cos * «j-f cos * ee-f cos1 a, = 1 А взаимная перпендикулярность единичных векторов / а / дает соотношение COS C08 + SOS COS p, 4-й по счету hoshα = 0. 0 * 3. Распространенный случай преобразования координат. Как и геометрия на плоскости, общий случай преобразования координат легко сводится к рассматриваемому конкретному случаю. То есть переместите начало координат в точку O (a, b, c) и получите новую систему координат из старой системы координат при следующем вращении системы. В результате новая ось отображается в таблице с заданным значением 320. Углы обзора> Начальная точка n *
2. Введите вспомогательную систему происхождения Ox и координаты Oxx * y * r \, оси которых параллельны старым осям Oy и Oz, и используйте старые координаты (x, Y * r) точки M в качестве вспомогательных координат представлять. Формула (3) с + л + х (6) B + y \ X *, yP, r * затем выражается как xlt yk1 gx в соответствии с уравнением (4). X * = Xx COb aj — \ — ухо a, COS ag, y * = xt cos fo + yt cos p, + r4 soe p „r * = xv cos Yt + yt cos + r% cos 7. Подстановка этих формул в (6) в конечном итоге xo-lH | soi ~ \ ~ yy cos 4-rx cos b |, Y = b + xx soe rd 4-й soe p, + rk cos p ,, * = C 4-xt cos 4-y soo Tt 4- rx cos 7 ..
Это общие формулы для преобразования координат в пространстве. Само собой разумеется, что девять косинусов этих выражений связаны шестью зависимостями (5). n * 4. Пример. 1. Придумай уравнение (8) r9 = ах где Af 0. Чтобы увидеть, какая поверхность соответствует этому уравнению, поверните систему координат вокруг оси Og на угол ^. Ось системы, возникающая в результате этого вращения, является сущностью Ohi Oyit Ozx (ось
Ozv — это то же самое, что и старая ось Oz). Таблица углов между осями выглядит следующим образом. Ой ой ой О ~ 4 1С т 1С 2 Ойт 3 * ‘4 * т 1С 2 Оз, * 2 ic 2 0 Легко увидеть из рисунка 320. Следовательно, уравнение (4) принимает вид: V2, V2 (8) Подставляя x, y и z в уравнение (9) ♦) (8) — уравнение косинуса. (9) 2. То же преобразование (9) преобразовать уравнение (10) z = ложь Где A * ф0 Α = 5-W-A).
Сравнивая последнее с §3 уравнением (22), мы видим, что гиперболический параболоид соответствует уравнению (10). *) Полученный результат следует сравнить с формулой § 3 (20).
Смотрите также:
| Прямая линия | Производные функции нескольких переменных |
| Поверхности 2-го порядка | Экстремальные значения функции нескольких переменных |
