Оглавление:



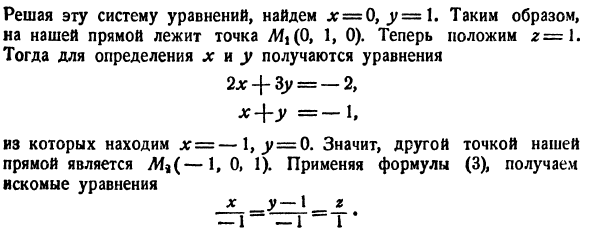





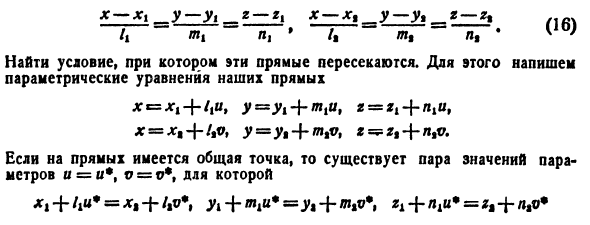












Прямая линия
- Прямая линия № 1. Каноническое уравнение прямой. Пусть p — прямая в пространстве. Выберите произвольную точку M0 (x r-, а условием для нахождения точки M на линии p является уравнение X X9_U U 9_2 / 14 Я-трет-р% Эти равенства называются стандартными Линия р уравнение знаменателя /, / I, l мы Это называется знаменателем индукции.
Надо помнить Это проекции векторов на прямую. Возьмите любое число lgo, yo, f, f, n (если хотя бы одно из последних трех не равно нулю) и запишите уравнение (i), затем пройдите через прямое каноническое уравнение, то есть точку Понятно, что у нас есть уравнение, которое Если он отделен от точки (г * y & z0) с помощью (x * y ^ z0), он имеет вектор {/, я,}}. Как обычно, исчезновение одного из знаменателей отношения (1) означает исчезновение соответствующего числителя. Например, уравнение Рисунок 302. ~
/ | w 4 L | ‘/ | / I | L | Для этого напишите параметрическое уравнение прямой x ^ Xg + ti и 9y ^ yi + mtu9 z = zl + niu, x = xt + Itv, y = y ”+ m% v, z = * zt-j-n, v. Если в строке есть что-то общее, пара значений параметров u =! Существует / •, v = r *. XJ + /! «♦ = *! + /,» ♦, yi + mku * =: yt + mxv \ + = ^ +
Найдите условие, где эти линии пересекаются. Людмила Фирмаль
ItU * -l% v * 4- (xk-x%) = 0, — + (Y4-A) = 0, (17) фи * — + (gx-z%) = 0 Вместо (17) рассмотрим систему однородных уравнений Uu-‘ftf + (* i-DG |) ® = 0, miff-m, t7 + (yt -yt) w = 0, (18) itjtf-n и + («j-r,) w = 0, Содержит другой неизвестный ш. Если существует числовая пара (u *, v *) t, удовлетворяющая соотношению (17), тройная цифра (uv \ 1) неочевидна (так как она содержит ненулевое значение w = ) системы Решение (18). Однако определитель системы (18) должен быть нулевым. 0 (19) U U xi — x * Щмт уу — у н т л. Zt — Z, Следовательно, если линия (16) имеет что-то общее, (19) должно быть выполнено. Наоборот, удерживайте (19).
Во-вторых, существует нетривиальное решение для однородных систем (18). Пусть (s0, v0 w0) — одно из таких решений. Указывает, что в нем есть w9 ^ t 0. L «# = mtu9 = mtvv Из чисел i / e одно ненулевое во всех случаях. ) [В противном случае (u ^ t? -, W0) является очевидным решением для системы]. Например, предположим, что ΦΦ0. Предполагая ^ ® = U = ql «t» 1 = Q * t * То есть тройка {/ „mltı4} пропорциональна тройке {/ тml„}, но это невозможно, поскольку прямая (16) не параллельна. w0jb (). Подставим u0, v0, w0 в (18) и установите полученный ID, деленный на w9
Приходите к (17). Следовательно, (19) гарантирует существование общей точки на прямой (16). Замечания. Условие, что прямая (16) не параллельна, выполняется. Фактически, в противном случае в определителе (19) первый и второй столбцы пропорциональны, а определитель равен нулю. Отказ от непараллельного предложения линии (16) приводит к (19) условию, что эти две линии находятся в одной плоскости. •) Между числом {/ 4, ty nt} и числом {/ „mv n9} существует ненулевое число, поэтому легко видеть, что оба они различны.
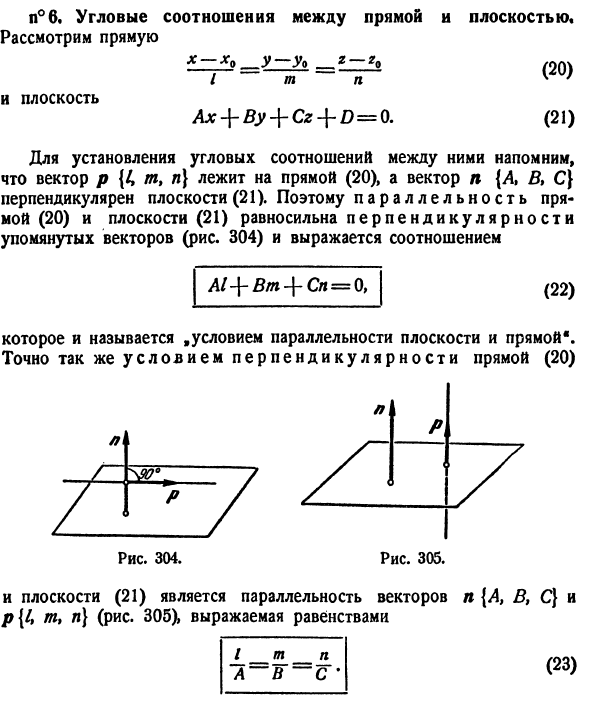
- n ° 6 — угловая зависимость между линией и плоскостью. Думай прямо V — V0 = в £ O m n (20) (21) И самолет x — \ — By — \ — Cz — \ — D = 0 (22) n P 1 / 1 Рисунок 305. L G ‘/ /> / Рисунок 304 Плоскость (21) является параллелизмом векторов n {A, B, C} и p {/, m, n} (рис. 305) и представлена уравнением Напомним, что вектор p {£ m, n] находится на линии (20), а вектор n {AB, C} перпендикулярен плоскости (21), чтобы установить угловую связь между ними , Следовательно, параллельность между линией (20) и плоскостью (21) соответствует перпендикулярности вышеупомянутого вектора (рисунок 304) и выражается следующим соотношением: Al + Bm + Cl = 0, Это называется условием параллелизма между плоскостью и прямой. «Аналогичным образом, состояние вертикальной линии (20)
Условия (22) и (23) допускают простую словесную формулировку, которую полезно запомнить. Условия параллельной обработки. Для параллельности, линий и плоскостей сумма произведений пар знаменателя направления линии и фактора направления плоскости должна быть равна нулю. Вертикальное состояние. Из-за перпендикулярности линии и плоскости, три знаменателя направления линии должны быть пропорциональны трем факторам направления плоскости.
В заключение рассмотрим, какой угол φ является прямой (20) с плоскостью (21). Из рисунка 306 видно, что угол <p является дополнительным углом 6, образованным векторами n {A, B, C \ и p {/, π, η}. так <р = 90 ° -0 И sincp == cos0. Однако для cos0 формула известна. Вот так Грех At + Bm + Cn UAY + VYA + SYAUR + t * + n * (24) м д / N / Рисунок 307. № 7 Расстояние от точки до плоскости и прямой линии. Давайте сначала посмотрим на пример.
Предположим, нам нужно найти расстояние d от точки M (3, 7, 1) до плоскости. Zx + Au-12g + 1 = 0 (25) Требуемое расстояние d равно расстоянию от точки M до точки N на пересечении перпендикуляра от M к плоскости (25), В этой плоскости (рис. 307). Это перпендикулярное уравнение (для прохождения M (3,7,1)) yag-3 _ y —7 _ 2—1 / t n 9 Кроме того, исходя из условия перпендикулярности (23), тройка направляющего знаменателя {4 rti, n} должна быть пропорциональна тройной направляющей плоскости {3, 4, -12} (25). Существует бесконечное количество троек {f, m, n1, каждая из которых определяет одну и ту же линию.
Предположим, нам нужно найти расстояние d от точки M (3, 7, 1) до плоскости. Zx + Au-12g + 1 = 0 (25) Людмила Фирмаль
Самое простое — сопоставить тройку {/, π, η) с тройкой {3, 4, -12}. Другими словами, напишите целевое уравнение. Рисунок 306.Перпендикулярно нам в форме х-3 у-7 з — 1 Если мы покажем сумму дробей, написанных буквой tf, мы получим параметрическое уравнение с вертикальной линией. * = 3-J-3f, z = 1- / 2t. (26) Как уже упоминалось, эти уравнения полезны для нахождения точки пересечения N между призмой MN и плоскостью. Замена (26)
В формуле (25), 3 (3 + 30 + 4 (7 -} — 40-12 (1-120 + 1 = 0, Откуда 169 * +26 = 0 о i t = — Подстановка значения f, найденного в (26), дает: 33 83 37 Координата номера точки x = \ 5 «z == l3 * ^ (33 83 37 \ 13 «13» TzG Вот так Соображения, которые следует учитывать при решении этого примера, могут решить проблему в общем виде.
Задача найти расстояние d от точки M (xv yv z9) до плоскости A * + By + Cz + £> = 0. (27) Решения. M (xv y \ z ^ Х- / т р Эта линия должна быть перпендикулярна плоскости (27), знаменателю m, n), чтобы эти тройки были пропорциональны тройке {A, D C}. Проще всего взять 1 = A, m = B> n = C. Следовательно, уравнение для перпендикуляра, упавшего с М на плоскость (27): X — x9 _ Y — Ush_r ~ r9
Чтобы найти точку пересечения N этого перпендикуляра и плоскости, нам нужно вместе решить уравнения (27) и (28). Для этого общее количество фракций (28) представляется как t. Это дает параметрическое уравнение для прямой WE. x = x9 + At, y = yQ + Bt, * = z0-fa. (29) Вставка этих величин в (27) дает A (xQ + At) + B (y0 + Bf) + C (z0 + Ct) + D = 0, (A * + & + (?) T + (Ax, +% + CZt + D) = Ot t _ Ax0 + By0 + Cz9 + D n
Это значение параметра t определяет точку N. Под буквой i в уравнении (29) это величина, определяемая уравнением (30), которая получает только координаты точки N слева. d = MN = V (x-xQr + (y-y »? + (2-z0) K уравнение (29) Сравнивая значение tt, полученное из последнего уравнения и уравнения (30), окончательно (31) Y A * + B * + Ca Следовательно, *), чтобы найти расстояние точки от плоскости, необходимо заменить координаты точки в левой части уравнения плоскости и разделить абсолютное значение полученного числа на квадратный корень из суммы квадратов направляющих коэффициентов. Пример.
Найти расстояние d между параллельными плоскостями **) Ax-j- By + Cz -f D = 0, Ax — \ — By — \ — Cz — \ — D * = 0 Решения. Получите точку M на второй плоскости (xe, jv. После этого требуемое расстояние — это расстояние от точки M до первой плоскости, поэтому оно выражается уравнением (31), но точка M Координаты A ^ + Bl + C ^ + A * -A Будете ли вы Топор + Vy9 — \ — Cr0 = -D \ И уравнение (31)
Определите прямую линию через точку (5, 3, 7) и содержащую ожидающий вектор {2, 0, 4} от этой точки. Этот вектор и линия (2) перпендикулярны оси Oy. Но в этом случае прямая находится в плоскости y = 3, поэтому -3 = 0 для всех точек на линии.
д = •) Полезно обратить внимание на этот результат и полную аналогию правила, чтобы найти расстояние от линии геометрии на плоскости до точки. • ♦) Конечно, коэффициенты x, y и r в обоих уравнениях не обязательно должны быть равными. Это потому, что условие параллельной плоскости гарантирует только пропорциональные отношения. Однако из-за этой пропорциональности всегда можно умножить одно из уравнений на определенное число, чтобы сделать вышеупомянутые коэффициенты равными.
Теперь рассмотрим проблему нахождения расстояния от точки до прямой. В общем, решение этого вопроса приводит к довольно громоздкой формуле и ограничивается указанием того, как проблема может быть решена в каждом конкретном случае. Расстояние от точки M (x * 9 y * 9 z *) до линии d (32) * o _U — Uo_z-zo ~ T ~ 90 ° (34) N Существует расстояние от M до точки N, где (Рис. 308) линия (32) пересекает плоскость, перпендикулярную ей, и рисуется Через М. Уравнение для этой плоскости: + m (y-y *) + n (z-z *) = 0. (33)
Точка N может быть найдена путем совместного решения уравнений (32) и (33). После этого известная формула применяется к расстоянию между двумя точками. Пример. Найти расстояние от точки М (2, 3, 4) до прямой x_y-2 г-7 Рисунок 308.1-О Решения. Уравнение плоскости через М и перпендикулярно прямой (34) имеет вид 1 • (L: -2) + 3-Cv-3) + 0- (L: -4) = 0 (35) Или то же самое JC + Zy = 11. Когда общее значение доли (34) представлено как t, x = U y = 2 — \ — 3 /, 2 = 7. Отсюда (от 35J 3 (2 + 30 = 11.
То есть * = координаты точки N: ^ y, 3y, 7j. d = MN = y (2- (3-3-7) * 3,39. В заключение отметим, что средства, описанные в этом разделе, могут решить проблему нахождения расстояния между двумя пересекающимися прямыми. Однако следующая глава решит эту проблему с помощью дифференциальных вычислений.
№ 2. Уравнение прямой через две заданные точки. Очень просто записать прямое каноническое уравнение через две заданные точки M \ (xv, yz,) и Afj (xy, y * z *). Фактически мы можем получить вектор MiM% = xXi y * — y Директор. Интересующая линия проходит через точку Mi (xXt ylt zt) t, поэтому уравнение линии (3) * — * 1_ Y — Y * i-xx Yy — Yx- № 3. Определение прямой по двум плоскостям. Рассмотрим две плоскости, которые не параллельны друг другу Alx + Biy + Ctz — {- Dx = 0, (4) A ^ x + By + Ctz + D4 = 0. (5)
Они пересекаются по линии р. Координаты любой точки на этой прямой удовлетворяют как уравнениям (4) и (5), так и наоборот, и все точки, координаты которых удовлетворяют обоим уравнениям (4) и (5), находятся на p Есть. Следовательно, пара уравнений (4) и (5) определяет прямую линию. Если вы хотите получить каноническое уравнение для этой линии, проще всего найти две точки над ней и применить уравнение (3). Пример. Напишите каноническое уравнение для прямой линии, которая является пересечением плоскостей 2x — \ — 3y — {- 5z-3 = 0, x + y + 2z-1 = 0. Решения. Установите z = 0. Предыдущее уравнение тогда имеет следующий вид: 2x — \ — Zy = 3
Решение этих одновременных уравнений дает * = 0 и ^ = 1. Следовательно, точка Afj (0, 1, 0) находится на нашей прямой. Тогда установите z = 1. Далее получаем уравнение для определения х и у 2x — \ — Zy = -2, х + у = -1, Отсюда найдите x = —1, ^ = 0. Таким образом, еще одна точка в линии — это Af9 (-1, 0, 1). Используйте уравнение (3), чтобы получить желаемое уравнение x y— \ _ g -1 ~~ 1 *
№ 4. Параметрическое уравнение прямой. Может быть полезно настроить линию немного другим способом без использования канонического уравнения (1). То есть, если линия р дается X-X0_v-y0_z-z0 0) N T Тогда для каждой точки (x, y, d) количество написанных минут имеет конкретное значение. Указывает это значение (для каждой точки!) При t. тогда х-х Я Откуда X = X0 + #> Y == Yo wtt z = Уравнение (6) называется параметрическим уравнением прямой р.
Они представляют задачи этой линии и были в виду выше. Чтобы получить все точки линии из (6), необходимо выполнить параметр t по всей оси значений. Полезно найти пересечение этой прямой и плоскости, используя параметрическое уравнение прямой. Пример. Найти пересечение косвенно х-г 3-4 ~~ 5 И самолет x ~ \ -2y-3r-2 = 0 Решения. Параметрическое уравнение для линии (7) имеет вид X = 2 — {- 3t, y = -l + 4f, z = 5t. Подставляя эти уравнения в (8), (2 + 30-b 2 (-1 + 40-с (50-2 = 0 или (6)
-At = 2 = 0, откуда т = —у. Далее уравнение (9) дает желаемую точку (4.-z. -4) — Конечно, предложенная задача может быть решена без перехода к линейному параметрическому уравнению (7), но она решает систему уравнений (7) и (8) напрямую, но применяемый метод упрощает расчет. Превращаться в № 5 Угловые отношения между линиями. Рассмотрим две строки L ~ и ~ I, Щпл в ‘ Напоминая, что векторы {/ „/ Wj, ||} и {4, Wj, / µ} находятся в строках (10) и (11) соответственно, сразу же получаются следующие результаты: I. Состояние параллельных линий.
Чтобы линии (10) и (11) были параллельны, одна тройка направляющего знаменателя должна быть пропорциональна другой тройке направляющего знаменателя. (12) =. / ■ ты (13) II. Вертикальное состояние линии. Чтобы линии (10) и (11) были вертикальными, сумма произведений их направляющих пар знаменателей равна нулю, 1 \ 1% -4-mx% -p == 0 III. Угол между двумя прямыми. Линия *) Когда выражено как угол между (10) и (11), cos e = -f- U ”+ mtma + ntn9 _ — + м? + l} • V11 + ml + nf
Выражение имеет двойную подпись, потому что записанная дробь является косинусом угла между векторами направления {/], mx, nx) и {4 м / м}. Угол между линиями ** не совпадает с углом между этими векторами и примыкает к нему (рис. 303). •) Если линии в пространстве не пересекаются, вам нужно провести две линии параллельно данным, проходящим через любую точку в пространстве. Угол между вновь нарисованными линиями называется углом между исходными линиями. * •) В конце концов, есть два таких угла (смежных друг с другом), и вы можете пнуть один из них на шесть.
Пример. Нарисуйте линию, параллельную линии, проходящей через точку М (2, 5, 4) 11 jc-Zu-3z -J-20 = O, * + Zy-6z + l = 0 » Решения. Сначала создайте каноническое уравнение для линии (16). Для этого найдите две точки. предположение z = 1 11l: -Zu = -17, x + 3y = b. Следовательно, x = -1, ^ = 2. Таким образом, Afi (-1, 2, 1) находится в (16).
Кроме того, если вы установите Z = 2, 1U-Zu = -14, Rns. 303.x + 3y = 11, 1 3 откуда х = — + — * Итак, вторая точка (15) M41— -j-, 3, 2j • Следовательно, каноническое уравнение для прямой (1 b) имеет вид х + 1 год — 2_g-1 % = ‘/ 4 G- 3 7 Ориентир здесь 1. Направляющий знаменатель должен принимать три пропорциональных значения. Выберите тройку {3, 7, 4}, чтобы получить ответ. 2 года-4 3 7 4 Рассмотрим следующий вопрос: задайте две прямые, параллельные друг другу
Смотрите также:
| Переменные векторы. Вектор-функции и их дифференцирование | Поверхности 2-го порядка |
| Плоскость | Преобразование координат |
