Оглавление:




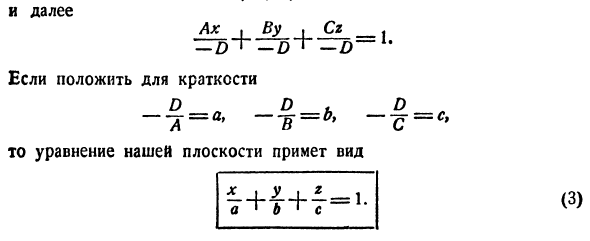



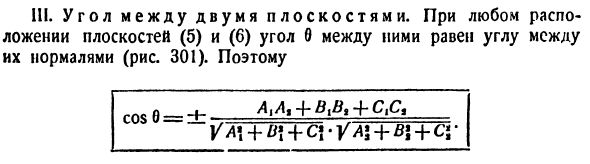


Плоскость
- самолет n ° 1. Плоское уравнение. Измените систему координат Oxyz в пространстве и рассмотрите плоскость P. Выберите точку M0 (Xq, yQ, z0) на P и нарисуйте M9. Вектор n = MQN, перпендикулярный плоскости P. Длина этого вектора не интересна и может быть выбрана произвольно. вектор MqN называется плоскостью нормальной R. A, B, C — Проекция Вектор MbN по осям Ox, Oy, Oz соответственно. После завершения этой предварительной конфигурации, получите любую точку M (x, y, z) в пространстве (не обязательно на плоскости!) (Рис. 297). Рисунок 297 очень четкий.
Точка M находится на плоскости P, только если векторы M% N и M0M перпендикулярны друг другу. Проекция вектора M0M на ось имеет вид X-X (py-yo, z-Zq, поэтому условие перпендикулярности для векторов M0L1 и M ^ N имеет вид 0) A (x-> oo) ^ (Y-Uo) ~ \ ~ C (Z- = Следовательно, точка M находится на плоскости P, только если ее координаты x, y, z удовлетворяют уравнению (I). Другими словами, уравнение (1) является уравнением для плоскости P. Зная, что порядок этого уравнения является первым, мы приходим к важной теореме, теореме /. Каждая плоскость соответствует линейному уравнению.
.Для полностью произвольного числа x9 A, B, C (но по крайней мере один из трех последних не должен быть равен нулю) уравнение (1) проходит через плоскость, т.е. точку y \ z0) Уравнение перпендикулярно вектору {AB, C}. Основываясь на этом утверждении, докажем теорему. Теорема 2.
Поскольку мы не изменили направление нормали, здесь был помещен двойной знак, и изменение любого из этих направлений заменило бы угол на is-8, тем самым изменив знак косинуса Людмила Фирмаль
К уравнениям первого порядка (2) x — \ — By — \ — Cz + D = Q (Хотя бы одно из чисел A, B, C отличное от нуля) соответствует плоскости. Фактически, используйте столько троек (x ^ z0), которые удовлетворяют уравнению (2) *). После этого Или в форме AXt + Byt + Cz0 + D = 0, откуда D = — (Ajc0 + + Cr0), уравнение (2) можно переписать в следующем формате: Ax + By + Cz- (Ax9 + Vy + Cz0) = 0, A (x-x,) — B (y-y °) + C (z-z0) = 0, И это уравнение вида (1), и плоскость фактически ему соответствует. Замечания. 1) Из доказательства теоремы 2 видно геометрическое значение коэффициентов A, B и C в уравнении (2). Это векторные проекции, перпендикулярные плоскости.
В этом отношении эти факторы называются направляющими. 2) Из предыдущего замечания видно, что вектор A = 0 и вектор {A B, C} перпендикулярны оси Ox, поэтому A = 0 и плоскость (2) параллельна оси ♦♦) Ox. Ситуация аналогична условию, что плоскость (2) параллельна другим координатным осям. Для полностью произвольного числа x9 A, B, C (но по крайней мере один из трех последних не должен быть равен нулю) уравнение (1) проходит через плоскость, т.е. точку y \ z0) Уравнение перпендикулярно вектору {AB, C}. Основываясь на этом утверждении, докажем теорему.
- Теорема 2. К уравнениям первого порядка (2) x — \ — By — \ — Cz + D = Q (Хотя бы одно из чисел A, B, C отличное от нуля) соответствует плоскости. Фактически, используйте столько троек (x ^ z0), которые удовлетворяют уравнению (2) *). После этого Или в форме AXt + Byt + Cz0 + D = 0, откуда D = — (Ajc0 + + Cr0), уравнение (2) можно переписать в следующем формате: Ax + By + Cz- (Ax9 + Vy + Cz0) = 0, A (x-x,) — B (y-y °) + C (z-z0) = 0, И это уравнение вида (1), и плоскость фактически ему соответствует. Замечания. 1) Из доказательства теоремы 2 видно геометрическое значение коэффициентов A, B и C в уравнении (2). Это векторные проекции, перпендикулярные плоскости.
В этом отношении эти факторы называются направляющими. 2) Из предыдущего замечания видно, что вектор A = 0 и вектор {A B, C} перпендикулярны оси Ox, поэтому A = 0 и плоскость (2) параллельна оси ♦♦) Ox. Ситуация аналогична условию, что плоскость (2) параллельна другим координатным осям.
Например, уравнение bx-3r — {- 7 = 0 соответствует плоскости, параллельной оси Oy. •) Это легко. На самом деле, скажем, Af0. Затем возьмем y9 и z0 произвольно и назначим их в (2), чтобы найти x0. Прямая в любой плоскости считается параллельной этой плоскости.
То есть, если одна из координат не вписывается в уравнение плоскости, плоскость параллельна соответствующей оси. Людмила Фирмаль
3) Если A = B = 0, плоскость параллельна осям Ox и Oy, координатной плоскости xy. Уравнение не имеет формы Cz + D = 0 или (в конечном итоге CfO) r = -ie 2 = С В частности, уравнение 2 = 0 является уравнением для самой плоскости xy. 4) Когда D = 0 в уравнении (2), точка 0 (0, 0, 0) находится на соответствующей плоскости, потому что три числа O, O, O удовлетворяют уравнению (2). Следовательно, уравнение D = 0 является условием прохождения плоскости (2) через начало координат. 5) (2)
Когда A = D = 0, соответствующая плоскость параллельна оси Ox и проходит через начало координат. Но тогда ось Ox находится на рассматриваемой плоскости. То же самое относится и к другим осям. Например, плоскость 5dr-3z = 0 содержит ось Oy. № 2. Плоское уравнение отрезка на оси. Давайте составим уравнение STI Ax — \ — By + Cg + D = * 0 (2) РИС. AOO, ВфО, СфО, DФ0, то есть плоскость не параллельна какой-либо координатной оси и не проходит через начало координат (рис. 298). Преобразовать выражение (2) в формат x — \ — by — \ — Cz = -D далее Ah By | Cg _. 1 Для краткости D p D Тогда уравнение плоскости имеет вид а 1 б 1 с
Последнее уравнение называется плоским уравнением отрезка на оси. Это имя объясняется тем, что знаменатели a, b и c являются отрезками, отрезанными от координатных осей плоскостью. Фактически, чтобы найти точку L (xL, yL, zL), где плоскость пересекает ось Ox, необходимо рассмотреть yL = zL = 0. Подставляя эти значения в (3), вы сразу видите xL = a. Пример. Для уравнения For: 5_y-72t 6 = 0, чтобы сформировать (3)
Эта задача решается путем последовательного преобразования. Bx — \ — by-7z = -6, -J-.J! __ l L— 1 Другое решение: установка y = z = 0 приводит к 3jc 6 = 0 и x = -2. Это отрезок в плоскости от оси Ox. Точно так же, b = -r = y, Это также приводит к (4). Хотя теоретическое значение уравнения (3) мало, это уравнение полезно для создания плоскостей на чертежах. № 3. Угловые отношения. I. Планарный параллелизм. Рассмотрим две плоскости P, + + + = a (5) Рис. 299. P * A * X 4-Btf + C, r + D9 = 0. (6) Если эти плоскости параллельны (рис. 299), их нормали также параллельны. То есть векторы «j [Al Bit Q} и n% {Ap Bp Ci) перпендикулярны плоскости.
То есть из-за параллельности двух плоскостей необходимо, чтобы тройка одного из их направляющих факторов была пропорциональна тройке другого направляющего фактора *). Условие (7) является параллельным условием для плоскостей (5) и (6). *) В этом случае следует помнить, что исчезновение числителя означает исчезновение соответствующего знаменателя и наоборот.
Например, гостиницы Zlg-5y + 6z-9; 6x— \ 0y 127-1-3 Ах: ах Для параллельного -5 -10 12 е 6 Аналогично параллельно плоскости 2x — \ — 3z —1 = 0, — {- 6z + 5 = 0, здесь 1-1L 4-6 И Би = Би = 0. 11. Требования к планарности. Если плоскости (5) и (6) перпендикулярны друг другу (рис. 300), их нормали ti \ {Ait Blf Q}, ttq {A%> B * C3} одинаковы. Но, как вы знаете. АхАш + ВА + САААА 0, То есть из-за взаимной перпендикулярности двух плоскостей сумма произведений их пары направленности должна быть равна нулю. Уравнение (8) является условием перпендикулярности плоскостей (5) и (6).
III. Угол между двумя плоскостями. Для расположения плоскостей (5) и (6) угол 0 между ними равен углу между их нормалями (рис. 301). так cos b = db VA \ + Vl + Cl-VAl + Bl + Cy
Смотрите также:
| Векторное произведение | Прямая линия |
| Переменные векторы. Вектор-функции и их дифференцирование | Поверхности 2-го порядка |
