Оглавление:




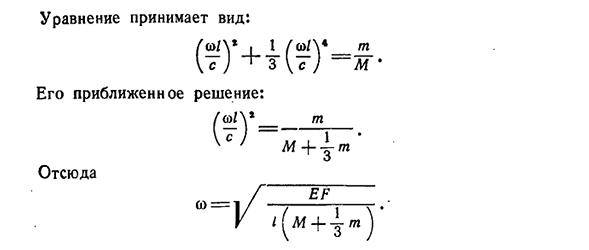

Продольные колебания стержней
- Продольная вибрация стержня. Теперь перейдем к исследованию колебаний систем с непрерывным распределением масс. Простейшим примером здесь является задача о продольно направленных колебаниях стержня определенного сечения. Для риса. 262 обозначены элементы стержня, которые в недеформированном состоянии были заключены между участками TP и pq с координатами x и x-\ — d x соответственно. Фиксируем несколько моментов времени t,
когда участок TP занимает позицию t’p’, участок pq-позицию p ’q’, обозначаем движение левого участка, исходные координаты XVI. Поскольку координата переменной времени T и неизменном х, смещение раздела координат х — \ — Д х а-\ — ^д-х. На этом же рисунке. 262 показывает элемент m’n’q’p’отдельно. Если вы представляете напряжение, действующее на секцию t’p ’с помощью a, напряжение, действующее на секцию p ’q’,
будет a — {- ^d x. но т р’ 777′ — у * ду п’ IP-и-Т* 7/7 р * ч’ — дуплексный л’х’ Рис, 262. Людмила Фирмаль
Уравнения движения и редукции Нарисованный элемент находится в движении С d*, его ускорение -, * масса qF dx, где q-плотность, а F-площадь поперечного сечения. Составим уравнение движения этого элемента:«. дА С. Однако, согласно закону крюка a=£e, относительный вариант элемента т р’ — тр Ди 8 — ———- ! Давай же! Тр ДХ F dx, получить: Здесь. dи 2_ _ d? И DH(175.1) Переходя к 30, отметим, что С — это скорость распространения продольной упругой волны.
Дифференциальное уравнение(175.1) называется волновым уравнением, которое описывает все виды динамических процессов стержня, распространения волн, колебаний. В § 30 мы рассмотрели проблему распространения волн, не прибегая к дифференциальным уравнениям, но теперь у нас есть возможность получить тот же результат другим способом. Действительно, мы удовлетворяем уравнению (175.1), поставив u=f(c t-x). Однако движение, описываемое этим решением, является распространением волн со скоростью С. Общее решение уравнения (175.1), принадлежащего Даламберу,
- имеет вид: «=/1(х/-х)+ / г(с/-}-х). (175.2)два члена — это две волны, бегущие с одинаковой скоростью в противоположных направлениях.§ 175] вертикальная вибрация штанги 38? Решение (175.2) является довольно распространенным в том смысле, что любое движение стержня может быть выражено таким образом, но простой метод обнаружения собственной частоты вибрации метод применения к задаче вибрации называется методом разделения переменных или методом Фурье. Во-первых, следует отметить, что уравнение (175.1) является линейным уравнением, решение которого имеет следующие бесспорные характеристики:1. Частное решение уравнения (175.1) было умножено. Опять же, любая константа является решением этого уравнения. 2. Сумма двух (и, следовательно, любого числа) конкретных решений является
решением. Здесь мы находим частичное решение уравнения (175.1)как произведение двух функций, T(t) и x(x).у=Т (Т)Х (Х). (175.3)заменить указанное выражение на и выражение (175.1): T X-CTX no=0. Точки здесь показывают производную от времени, а штрихи-производную от координат. Деление переменных заключается в том, что уравнение записывается как: Первый член-функция времени, второй член-функция координаты x, и уравнение возможно только в том случае, если каждая из этих функций постоянна. Таким образом, co’это константа. В случае функции T (t) M X (x) мы уже получаем нормальное дифференциальное уравнение следующего вида: (175.4) X » +J^=0. (175.5)) Общий Интеграл первого уравнения: потому что со|В-/ — в Т-грех. Таким образом, можно видеть, что со представляет собой круговую частоту свободных колебаний. Осталось определить функцию L»(x). Общий Интеграл уравнения (175.5): .1sin-с-Л1-
С потому что. 1. C (175.6) 384 сопротивление материала динамической Людмила Фирмаль
задаче[глава XVI При определении констант этого уравнения из граничных условий мы сталкиваемся с той же ситуацией, что и при решении задачи устойчивости (§ 136). Константы C и C определяются на основе однородных граничных условий, и выводятся однородные уравнения с тривиальными нулевыми решениями. Нетривиальное решение существует только для и определенного значения, которое является»это собственная частота. Прежде чем перейти к этому примеру, давайте рассмотрим возможные типы граничных уравнений: а) Z a к R e n L e N s y к o n E C, I=0,
и следовательно X=0. b) C V o b o d n y K o n e C. C=0, поэтому e=|^=0, T(t) вообще не равно нулю, поэтому X=0. Применяя принцип Д’Аламбера, сила инерции груза равна внутренней силе конца.: — М^ТТ-ф г-е^ -, ДТ * ДХ * Или — М Т Х=Е Ф Т Х’. Здесь мы используем общий множитель 7′ (/), чтобы исключить T. Get: Икс — Уравнение (175.4) и редукция М * ПФ?» Х=0. В качестве примера рассмотрим задачу о колебательных стержнях длины I, в которых один конец закреплен, а другой конец имеет массу массы M. Если вы поместите начало координат в точку x=0, то сразу увидите, что константа SG в уравнении (175.6) равна нулю. Альтернативное значение-… В конце WX, nie X=C g s in-B
граничное условие x=1, если нагрузка связана, находим: «Сотрудничество г/м, соль п С, С, с——— = — грех — =0. 1л с ФК С с Дж Если C—0, то вибрации нет, и вибрация возникает только тогда, когда кронштейн исчезает. Масса стержня представлена t, m=QFl. Тогда уравнение для решения принимает вид: (175.7)§ 175] продольное качание штанги 385 Это трансцендентальное уравнение имеет бесчисленные корни, а собственная частота системы бесконечно велика. Графическое определение корня
производится так, как показано на схеме. 263; значение удовлетворяющего выражению Y (175.7) является абсциссой пересечения кривой j=t g^с гиперболой: Т ал При очень больших значениях гипербола находится очень близко к горизонтальной оси, а абсцисса пересечения гиперболы с касательной лишь незначительно отличается от ПЛ. Таким образом, на высоких
частотах получено асимптотическое выражение (175.8) При достаточно большом n собственная частота, определяемая по приближенной формуле (175.8), мало отличается от ее точного значения. В предположении, что масса стержня меньше массы груза, вычисляются собственные частоты основного звука. После этого<o/ — — — — — небольшое количество и уравнение можно записать в виде Рис, 263. (175.7)в первом приближении После очевидной трансформации она продолжается: Но значение таких собственных частот
мы получим, учитывая изменчивость систем С одной степенью свободы, то есть ядро лишено массы и эндоплазматического ретикулума.: 13ю. Н. Работнов386 динамические задачи[гл. XVI Уравнение принимает вид: ) +3~ ~ 1л’ Его примерное решение: / и! у меня т+^т’ И так оно и есть. «=/ТРТР»
Смотрите также:
| Формула и способ Релея | Поперечные колебания стержней |
| Нижние оценки для частоты основного тона | Колебания балок постоянного сечения |
