Оглавление:





Равновесие гибких нерастяжимых подвесных нитей. Основные определения и зависимости
- Рисунок 13. 1. С — нижняя точка В инженерных сооружениях необходимо непрерывно распределять по всей длине резьбу, находящуюся под воздействием вертикальной нагрузки, на цепь или трос, подвешенные на концах между 2 опорами рис. 13. 1. Рассмотрим задачу, в которой задано значение span, sag, d, а также показатель распределенной нагрузки aa b b. При изучении равновесия цепей или тросов, как правило, необходимо ответить на 2 вопроса.
Какова будет форма кривой, которую цепь или трос принимает в положении равновесия 2 Насколько велико натяжение цепи троса в любой точке по длине кривой Чтобы ответить на поставленный вопрос, рассмотрим равновесие некоторых частей потока cd рис. 13. 2, а. Т. Точка d — это любая точка в потоке, имеющая координаты x и y. Направление осей отображается в том же месте.
При проектировании двигателей, машин и механизмов, мостов и других сооружений всегда производятся расчеты на колебапия. Людмила Фирмаль
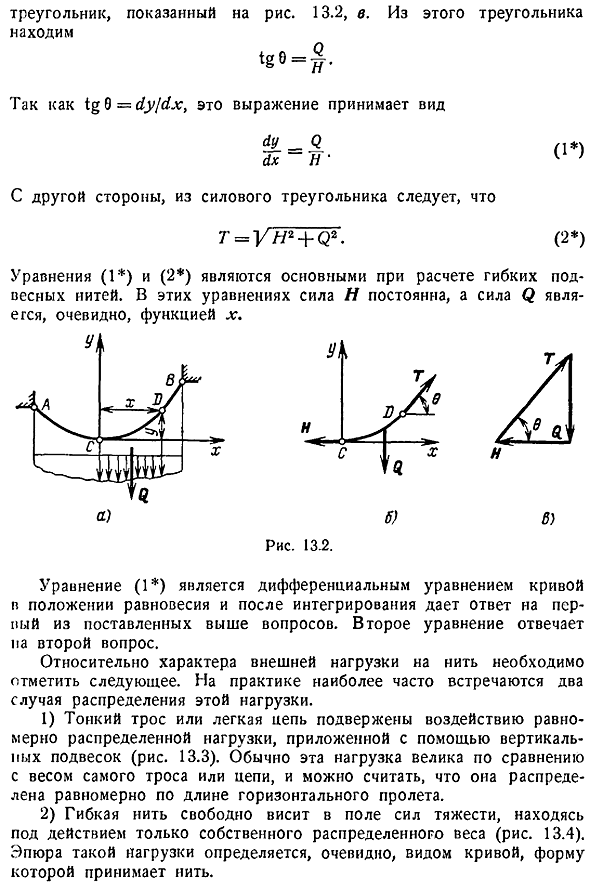
Отрезанный участок cd, который можно считать твердым телом на основе принципа затвердевания, находится в равновесии под действием 3 сил вертикальной силы q которая является результатом распределенной нагрузки участка c, и со сторон каждого отброшенного участка 2 растягивающих силы h и t нитей, которые представляют собой реакцию рис. 13. 2, силы h и t касательны к кривой вокруг точек c и d. Вертикальная сила q проходит через центр тяжести той части диаграммы, которая находится между рассматриваемыми участками. Эти 3 силы должны образовывать замкнутую силу Отображение треугольника Рисунок 13.
Из этого треугольника поскольку tg 9 rfy rfx, эта формула принимает вид dy Д ДХ ч С другой стороны, это следует из треугольника силы Т Нет. К2. Я 2 Уравнения 1 и 2 являются основными при расчете упругой подпружины threads. In в этих уравнениях сила h постоянна, а сила q, очевидно, является функцией x. А б Рис. 13. 2. Уравнение 1 является дифференциальным уравнением кривой в положении равновесия, которое после интегрирования дает ответ на первый вопрос выше.
- Выражение отвечает на 2-й вопрос. Что касается характера внешней нагрузки на резьбу, то следует отметить следующее. На самом деле чаще всего встречаются 2 случая такого рассеивания нагрузки. 1 тонкий трос или легкая цепь подвергаются равномерно распределенным нагрузкам с помощью вертикальной подвески рис. 13. 3. Как правило, эта нагрузка больше, чем вес самого кабеля или цепи, и можно предположить, что она распределяется Лена равномерно по длине горизонтального пролета. 2 гибкая нить висит свободно в поле тяжести и находится под действием только собственного распределенного веса рис. 13. 4. График такой нагрузки четко определяется типом кривой, то есть формой, которую принимает нить.
В первом случае нагруженная гибкая нить принимает форму параболы, а во 2-м случае-а chain-line. It показана основная формула для определения характеристик резьбы в обоих основных случаях. Парабола. Если пряжа равномерно распределена по размаху вертикальной нагрузке прочности q рис. 13. 3, то уравнение кривой равновесия пряжи в выбранном направлении —- Формат координатных осей Натяжение нити вдоль кривой изменяется в соответствии с Формулой 2 t un dxg, 4 Таким образом, натяжение нити будет минимальным в самой нижней точке c равной h, увеличивающимся к концу нити и максимальным в верхней опоре.
Как известно из курса аналитической геометрии, уравнение (22) является уравнением кривых второго порядка в полярных координатах. Людмила Фирмаль
Натяжение конца нити в каждой из точек a и b Равный Альта-ВН д Ар, ТБ v т-п кв 5 Здесь расстояние от нижних точек c до опор a и 8, a и b, определяется из уравнения. Или из уравнения 6 а 6 6 Все e их уравнения остаются неизвестными Н. Минимальное напряжение определяется по формуле П 2 k, j2 В этом уравнении знак плюс соответствует случаю, когда вершина параболы, определяющая положение равновесия нити, находится между опорами, как показано на рисунке. Знак минус относится к случаю, когда вершина параболы находится на одной стороне обеих опор. Важно в определенных случаях, если оба поддерживают одно и то же Уровень у нас есть Цепная линия.
Предположим, что нить свободно подвешена в поле силы тяжести, и она получает только свой собственный вес, равномерно распределенный по длине нити рис. 13. 4. Введем следующие обозначения. 7-вес длины резьбы, а s-длина дуги cd. Тогда соотношение между координатами s и x точки d задается формулой. 8 Длина резьбы l между опорами равна Форма уравнения кривой равновесия координатных осей имеет вид При выборе 9 Направление 10 Это уравнение оси цепи с вертикальной осью. Натяжение нити в любой точке d равно tor n Это так. O из этой формулы следует, что натяжение t будет минимальным при нижнем с резьбы, равным h, увеличивающимся до конца нити и достигающим максимума при верхней опоре.
Натяжение на краях a и b равны соответственно ТП ч qfb 12 Если вы хотите определить расстояние b, вам нужно использовать формулу Бассейн Предопределенный Г — Ипелорик. 3н р — н — Наконец, значение h определяется из выражения с. Используйте таблицу гиперболических функций. При решении задач с равновесием гибкой системы необходимо 1 определить вид нагрузки, действующей на резьбу собственный вес, равномерно распределенный по всему горизонтальному пролету и т. 2 Выберите систему координат и создайте дифференциальное уравнение равновесия нити и уравнение натяжения g. 3 интегрируем уравнение равновесия и находим уравнение, равное пружинной кривой нити.
Смотрите также:
Предмет теоретическая механика
| Устойчивость движения по первому приближению | Параболическая нить |
| Устойчивость движения при наличии гироскопических сил | Цепная линия |
