Оглавление:







Резонанс в нелинейных колебаниях
- Нелинейный вибрационный резонанс. Включение ангармонических терминов в вынужденные колебания системы открывает принципиально новую функциональность Особенности резонансного явления. Добавьте внешний период в правую часть уравнения (28.9) Получить силу (частота у) x + 2 \ x + o) qX = cosyt-ax2- [3×3; (29,1)
Сила трения также записывается здесь с показателем демпфирования A (при условии, что он ниже). Строго говоря, если в уравнении свободной вибрации учитывается нелинейный член, то член высшего порядка амплитуды движущей силы также должен учитываться, что соответствует возможности зависимости от смещения x.
Чтобы выяснить природу результирующего движения Людмила Фирмаль
Эти члены были созданы не только для упрощения формулы. Они не меняют качественный взгляд на явление. Дай мне у = W0 + Ј (Малое е), то есть мы близки к обычному резонансу. , прямое исследование уравнения (29.1) может быть опущено, если используются следующие соображения.
В линейном приближении зависимость амплитуды b Внешняя сила амплитуда / частота вибрации Это дается вблизи резонанса уравнением (26.7). B2 (e2 + A2 Вибрационная нелинейность приводит к появлению зависимости Их собственная частота против амплитуды, напишите на форме Шоу м2 (29,3) где является константой и представляется определенным образом через ангармонические коэффициенты (см. (28.13)).
- Поэтому замените это формулой (29.2) (точнее, с небольшой разницей y-sio) sio to sio + b2. Сохраняя обозначение Ј = y-wo, Формула 2 „3 [(Ј _ ^) 2 + Л2] = _ 1 _ (2М) или e = „b2 ± J (-J—) 2-X2. у \ 2та) б) Формула (29.4), куб относительно b2 и его сущность Естественный корень определяет амплитуду вынужденной вибрации. Для данной силы / амплитуды учтите, что эта амплитуда зависит от частоты внешней силы.
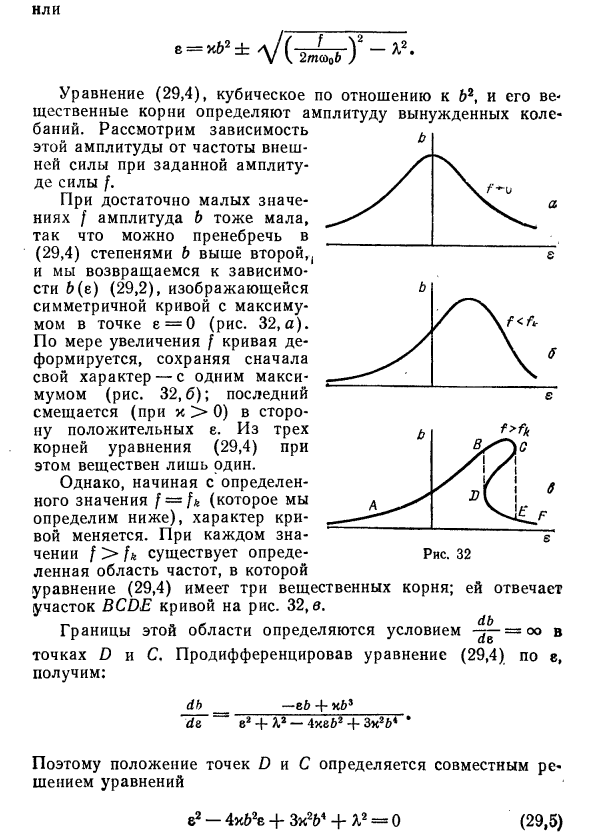
Если значение / достаточно мало, амплитуда b также (29.4) игнорирует второй более высокий порядок b и возвращает зависимость b (e) (см. (29.2)). Это представлено самой большой симметричной кривой в точке Ј = О. (Рисунок 32а). Когда увеличение / кривая деформируется, Сначала раскрыть ее характер до одного (рисунок 32b) \ Последнее смещается в сторону положительного е (когда к> 0). Из трех корней уравнения (29.4) существует только одно действительное число.
существует конкретная частотная область с тремя действительными корнями Людмила Фирмаль
Тем не менее, конкретное значение / = / & ( Свойства кривой изменятся, как определено ниже. Для каждого значения f> fk в уравнении (29.4) существует конкретная частотная область с тремя действительными корнями. Соответствует части кривой BCDE на рисунке 32 в.
Граница этой области определяется условием db / dt = os в точках D и C. Дифференцируя уравнение (29.4) db _ —sb + xl dzЈ2 + A2-4 xeb2 + 3 x 2b4 Поэтому расположение точек D и C определяется совместным решением уравнения. e2-4xB2e + 3x 2b4 + A2 = 0 (29,5) А (29.4); соответствующее значение Оба положительные.
Достигните максимальной амплитуды в точке Где дб / дт = 0 Кроме того, Ј = xb2, а из (29,4) есть (29.6) 2shsioa Это значение соответствует максимальному значению, данному зависимостью (29.2). Вы можете показать (не останавливайтесь здесь х)
Среднее из трех реальных корней формулы (29,4), среднее (То есть график кривой CD, показанный пунктирной линией на рисунке 32. Линия) соответствует нестабильной вибрации системы: любое слабое влияние на систему в этом состоянии приводит к переходу в режим вибрации, соответствующий большим или меньшим корням (т.е. Кам солнце или DE).
Следовательно, фактическая вибрация системы соответствует Существуют только ветви ABC и DEF. Отличные особенности В этом случае существует частотная область, которая принимает две разные амплитуды колебаний.
Следовательно, когда частота внешней силы постепенно увеличивается, амплитуда вынужденной вибрации увеличивается в соответствии с кривой ABC. В точке C происходит «пробой» по амплитуде, который резко падает до значения, соответствующего точке E, а затем (когда он увеличивается далее) Частота) изменяется вдоль кривой EF.
Если сейчас снова Когда частота снижается, амплитуда вынужденной вибрации det изменяется вдоль кривой FD, скачет к B в точке D, а затем уменьшается вдоль B A. Для расчета значения / & это Значение / — значение, при котором оба корня вторичного (b2) выражения (29.5) совпадают. Если / = /, весь раздел CD сводится к одной точке перегиба.
Если дискриминант квадратного уравнения (29.5) равен нулю, то получается r2 = ZA2. Соответствующий маршрут Уравнение: k2 = 2e / 3. Подставляя эти значения b и b в (29.4), Вы найдете fk = (29-7) С изменениями в природе резонансных явлений Частота y, si, колебательная нелинейность
Появление нового резонанса, который генерирует вибрации с частотой, Близко к sio, возбуждается внешней силой на частоте, значительно отличающейся от s o o Частота внешней силы yssio / 2, Y = ci0 / 2 + e.
В первом линейном приближении вибрация системы возбуждается с той же частотой и амплитудой, пропорциональной амплитуде силы х <1) = z ^ rH? + Ј) * (Согласно формуле (22.4)). Тем не менее, при рассмотрении нелинейных условий, Во втором приближении эти колебания приводят к появлению члена с частотой справа от уравнения движения (29.1). 2y «sio- т.е. присваивать выражению 2 (2) + 2Ax (2) + ao2xM + axx ^ 2 + M 2) 3 = — 0, если k <0, кривая обратная. Side).
Из точки в л с Постоянное значение = ± J (^ L _ V \ 3 м> о -AX2. ч 3771CUq / С левой стороны точки B возможно только значение b = 0. Нет резонанса и вибрации частоты следующего порядка Шоу не взволновано. В интервале B l C есть два маршрута: b = 0 (сегмент BC на рисунке 33) и уравнение (29.13) (ветвь BE).
Наконец, справа от точки C есть все три маршрута (29.12) — (29.14). но Не все эти значения соответствуют стабильному режиму вибрации. Значение b = 0 нестабильно в области самолета х) Это также показывает, что система, соответствующая маршруту (29.14) (две другие средние точки), всегда нестабильна. к Нестабильное значение 33 на фиг. B обозначено пунктирной линией.
Например, во-первых, «поведение покоя «2) Система, в которой частота внешних сил постепенно уменьшается, пока не будет достигнута точка C, b = 0, и это состояние« разрушается »с переходом в ветвь EB. При дальнейшем уменьшении ampl амплитуда колебаний уменьшается до нуля в точке B.
Когда частота увеличивается, наоборот, амплитуда колебаний увеличивается вдоль кривой BE 3. Рассмотренные случаи резонанса являются основными Происходит в нелинейных вибрационных системах. В более высоких приближениях резонансы появляются на других частотах. Строго говоря, резонанс должен возникать на любой частоте y, n y + w c и o = cuo (где n и m — целые числа). Для любого y = pwo / q p и q снова являются целыми числами.
Однако по мере увеличения степени приближения интенсивность явления резонанса (и ширины частотной области, в которой он возникает) быстро уменьшается, Только резонанс наблюдается на частоте rp0 jq, где значения p и q малы. Оспаривать Определить резонансную зависимость b (e) на частоте Решения.
В первом приближении х ^ = -ф 8mcUn s [(3sh0 + e) t . Для второго приближения (x ^) получим уравнение из (29.1) x ^ + 2Azh ^ + o) qX ^ + осх + | Зж ^ 3 = -3 | 3ж ^ ж ^ 2, Только терминология написана с правой стороны равенства, что приводит к рассматриваемому резонансу. Вставьте x (2) 6 cos и извлеките резонансный член из произведения трех косинусов.
Уравнение представления 3 (3 b2f } 2 (exp23 [(26 Это зависит от числа 6, но от выражения (29.4) / 3 (362 // 3 2 куб.кв) и Ј / 3: -B Корень этого уравнения ЈA 9 | 32/2 212sh2si! : B4 = ^ 4b4. Рисунок 34 Зх + 2х2 ± к EA A2 Zs 4×2 • A2. Рисунок 34 показывает Зависимость от зависимости 6 (если x> 0).
В стабильном режиме поддерживаются только значение 6 = 0 (горизонтальная ось) и ветвь AB. Точка А соответствует значению = 3 (4x2A2-A2, 2_4x A + A ’A su 4bk -4 us2 A Режим вибрации Ј> Ј *. , А амплитуда 6> 6fc. Поскольку состояние 6 = 0 всегда стабильно, для возбуждения вибрации требуется начальный «толчок».
Полученное выражение допустимо только для небольших форов. Если амплитуда силы соответствует требованиям, малость пятки гарантируется малостью A. Wii A2 / sio A / x si o •
Смотрите также:
| Параметрический резонанс | Движение в быстро осциллирующем поле |
| Ангармонические колебания | Угловая скорость в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.
