Оглавление:









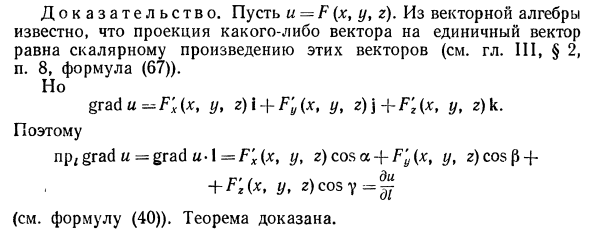







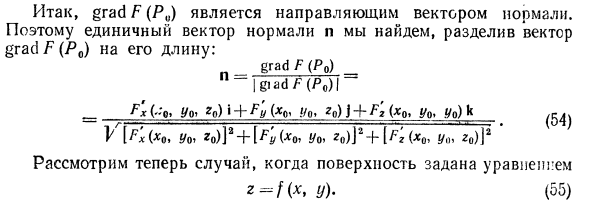

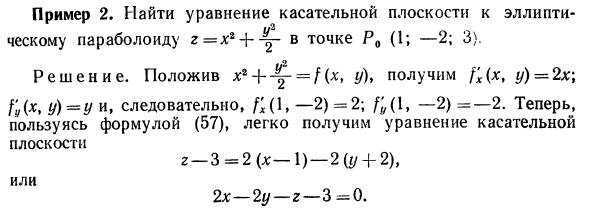

Скалярное поле
- Скалярное поле /. Скалярные поля и их геометрические изображения Определенное скалярное поле является частью пространства (или всего пространства), и каждая точка P соответствует числовому значению скалярной величины. Например, неоднородный объект, в котором каждая точка соответствует определенному значению плотности, можно считать скалярным полем.
Во всех случаях предположим, что скалярная величина не зависит от времени, только положение точки P в пространстве. Другими словами, величина рассматривается как функция точки P \ u = * F (P). Эта функция называется полевой функцией. Вводя систему координат Охуга в пространстве, точка P этой системы имеет конкретные координаты x, y, и скалярная величина является функцией этих координат. И -F (P) -F (x, y, r).
Другими примерами скалярных полей являются поле распределения температуры и поле потенциального распределения данного объекта. Людмила Фирмаль
градиент Скалярные полевые исследования рассматривают градиент определенного вектора, скалярное поле, тесно связанное с этой функцией, наряду с полевой функцией u = F (x, £ /, 2). Определение Градиент точки P (x, y, z) в скалярном поле, определяемом дифференцируемой функцией u = F (x, y, z), представляет собой вектор, равный F’x (x, y, z) \ + Fy (xf y, z) j + F; (x, y, z) k. Наклон функции u-F (x, y, r) обозначен одним из символов. град F (х, у, 2), град F (P). По определению grad F (x, * /, z) = F’x (x, y, z) \ + F’y (x, y, z) j + (x, j /, z) k. (42) Таким образом, для каждой точки P (x; z) скалярного поля, определяемой дифференцируемой функцией u = F (x, y, r), не только значение этой функции, но и четкий вектор grad F (P) Он включен.
Пример 1. Найти градиент функции u — x2 — \ — 2y2 — z2-5 в точке P0 (2; -1; 1). Решения. Если мы введем обозначение F (x, y, r) = x2 + -z% -5, мы найдем F’x (x, y, r) -2x. F’y (x, z) = 4f /; Fz (x, y, z) = — 2z. Затем используйте уравнение (42), чтобы получить: grad и (P0) = F’x (2; -1; l) i + 7i (2; -1; 1) j Z Z7; (2; -1; l) k ~ = 4i-4j-2k. Градиент функции u = F (x, y, z) в данной точке и Ди Это является исчерпывающим в том направлении, что связь, установленная следующей теоремой, находится в той же точке. Проекция вектора теоремы grad и единичного вектора 1 = cos a-i- | —f-cos p • j + cos y • k равна производной функции в направлении I. нп.град и = q ~. (43)
| Полный дифференциал функции | Экстремум функций двух переменных |
| Дифференцирование сложных и неявных функций | Тройной интеграл |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Доказательство. Пусть u = F (xt y, r). Из векторной алгебры известно, что проекция вектора на единичный вектор равна скалярному произведению этих векторов (см. Гл. III, § 2, стр. 8, уравнение (67)). но grad u = F’x (x, y, z) \ + F’y (x, y, z)] + F’2 (x, y, z) k. так np, grad u = grad, A = F’x (xt y, z) cos a -f F’y (xt y, e) cosp-f- -j-F’Ax, y, z) cos y (см. уравнение (40)). Теорема доказана.
Тогда pr, grad, and- \ grad w | .cos <p. Следовательно, основываясь на уравнении (43), = | С выпускниками | cos ср. (44) Если вектор I и направления grad и direction совпадают (<p = 0), то производная по направлению ^ имеет максимальное значение, которое явно равно |. Выпускники | cos 0 = | Выпускники | Таким образом, следующий вывод сделан. Град — это вектор, который указывает направление максимального увеличения поля в конкретной точке и имеет модуль, равный скорости этого увеличения.
Учитывая, что производная направления u представляет скорость изменения скалярного поля u — F (x, y, r) в этом направлении, уравнение (43) можно прочитать как у, г) направление вектора IЛюдмила Фирмаль
Таким образом, функции града и скалярного поля u-F (x, y, r) определяются самим полем и не зависят от системы координат, в которой рассматривается полевая функция. Найти относительное положение grad u = grad F (x, y, z) в данной точке P0 (x0; y0 \ r0) и горизонтальной плоскости, которая проходит через эту точку. Это поверхностное уравнение имеет вид F (x, y, z) = C0 или F (x, y, z) —Co = 0. (45) Рассмотрим кривую L на поверхности (45), проходящую через точку P0 (рис. 224). Рассмотрим эту кривую
Определяется уравнением х * = х (т), ‘ у = у (т), (46) z = z (0,> Где x (l), Y (0 и z (/) — дифференцируемые функции от /, x0 = x (1n), yQ = y (t0)> z0 = z (t0). Каждая точка имеет координаты. Кривая L полностью находится на этой поверхности, поэтому Y (O и MO «должны удовлетворять уравнению горизонтальной плоскости (45). Следовательно, тождество F [x (t) t y (t), z (t)] — C0-0. Используя формулу (34) (см. § 5, подраздел 1), рассматривая обе стороны этого тождества по t, учитывая (C0) ‘ ^ W + JfTW + S’-W-O. Специально для / — / „ F’z (x.> Yo * * o) x ‘(* o) + P’y (x0 »Yo> r *) y’ Yo) + P’r (Xo * Y0. Gv) r ‘(/ in ) «0. (47) Левая часть этого уравнения является скалярным произведением grad u (P0) -F’x (x0t y0, z0) \ + F’y (x0t y0, z0) i + F’2 (x0t yot r0) k и вектор r ‘(.) «» (/.) 14 В (до)) + *’ (футы) k, Ориентирован по касательной кривой L (см. Главу VI, § 5, стр. 3). Вот так град и (Po) -r ‘(/ „) = 0. (48)
Предположим, что grad u (P0) Φ0. Тогда из (48) в градус u (Pq) перпендикулярно вектору r ‘(f0) и касается кривой L в точке P0. Поскольку эта кривая была выбрана произвольно, мы приходим к следующему выводу: Скалярное поле задается дифференцируемой функцией u = F (x, y, r).
Далее все касательные, нарисованные на линии, которая находится на горизонтальной плоскости на уровне P0 и проходит через точку p0, помещаются в одну плоскость, перпендикулярную вектору gradF (P0), если только этот вектор не равен нулю. Для плоского скалярного поля, определяемого дифференцируемой функцией двух переменных r = f (x, y), наклон определяется как grad / (xt y) = /; (x, * /) i + /; (x, //) j. (49) Связь с производной в направлении U выражается уравнением А 62 нп / град ^ =,
или u = | выпускник 21 cos f, Где φ — угол между единичным вектором 1 и градиентом. Если поле задается дифференцируемой функцией r (y), вектор grad f (xot y0) оказывается перпендикулярным касательной, нарисованной на линии уровня в точке P0 (x0 \ y0). Пример 2. Найти максимальную скорость нарастания функции »r = x2y — 5y * в точке P0 (2; 1). Решения.
Максимальная скорость увеличения функции равна модулю наклона этой функции. узнать grad r = (x * y-5y3) ‘xi + (xy-5y% J-2xyi + (x * -15y *) J. В точке P0 (2; 1) град r = 4i-llj. В результате максимальная скорость увеличения * функции составляет grad r | Pe = V \ r -f-112 = V 137. 4. перпендикулярно касательной плоскости и поверхности Поверхность задается уравнением f (x, y} 2) -0, (50)
Слева находится функция, которую можно дифференцировать в конкретном регионе. Эта функция u = F (x, y, r) определяет скалярное поле, где заданная поверхность (50) является одной из поверхностей уровня *. Предположим, что в точке P0 (x0; y0 \ r0) град F (x, y, z) не равен нулю.
Тогда и согласно. Как показано на фиг.3, все касательные линии, нарисованные на поверхности (50) и нарисованные в точке P0 относительно линии, проходящей через точку Pn, расположены в одной плоскости, перпендикулярной градиенту F (P0). Эта плоскость называется касательной плоскостью поверхности F (x, y, r) = 0 в точке P0 (x0 \ y0; r0) (рис. 225). Касательная поверхность gra ; Y0 \ 20), поэтому уравнение имеет вид Рисунок 225 (51) A (x-x0) + B (y-y0) + C (r-r0) = 0
(См. Главу IV, § 1, пункт 2, формула (4)). вектор grad F (Pn) = F’x (n’0, y0, z0) \ + F’y (x09 y0, r0)} + F’2 (xot y0, r0) k В зависимости от условия он перпендикулярен касательной плоскости и может рассматриваться как нормальный вектор этой плоскости. То есть, от A до FX (x0, y0, z0), от B до Fy (x0, y0, 20), C = F’z (x0, y0, r0). В этом случае уравнение (51) принимает следующий вид: F’A * »V0> z0) (x-x0) + F’y (x0, y9, r0) (y-y9) + A-F’Axo, y0, z0) (z-z0) = 0. (52) Это уравнение касательной плоскости поверхности (50) в точке P0 (x0, y0, r0).
Предположим, что в точке P0 (x0, yn, rn) имеется касательная плоскость с поверхностью (50). Прямая, проходящая через точку P0, перпендикулярную этой касательной плоскости, называется нормалью поверхности (50) в точке P0 (x0, * / 0, z0). Вектор gradP (P0) четко ориентирован вдоль нормали, поэтому его можно использовать в качестве направляющего вектора. Следовательно, нормальное каноническое уравнение имеет вид , * — * »^, =, R ~ r °. (53) Ex * y0, z0) Fy (x0, y0, r0) F2 (x0, y0, r0) Пример 1. Найти уравнение x2 — \ — 2 y2-r2-5 = 0 в точке Po (2; -1; 1) и нормали касательной плоскости и гиперболоида 1-го листа.
Решения. В разделе 3 (см. Пример 1) был найден наклон функции F (x, y, z) -x2 2y2 — z2-5 в точке P0 (2; -1; 1). Кроме того, было обнаружено, что gradf (P0) = 4i-4j-2k. Таким образом, искомое уравнение для касательной плоскости и нормали имеет вид: 4 (х-2) -4 (у + 1) -2 (г-1) = 0, или 2x — 2y-2-5 = 0 (уравнение касательной плоскости); x — 2_y-H _g — 1 4 —4 —2 ‘ или х — 2 и + 1 г — 1, ч — = — (Нормальное уравнение).
Поэтому grad F (P „) является вектором нормалей, указывающим направление, поэтому единичный вектор нормалей n получается делением вектора grad F (P0) на его длину. выпускник F (po) _ -Y * + Yo * o) J. + Fi ^ o, Yo, «o) k ^ V [F’x (x0, + V0> «e) Ja + | ^ * (* o. V0> * o)] 2 Теперь рассмотрим случай, когда поверхность задается уравнением z = f (x, y). (55)
Наоборот, все функции трех переменных u = F (x, y, z) определяют какое-то скалярное поле. Скалярные поля часто представлены геометрически с использованием так называемых поверхностей уровня. Определение Скалярная поверхность уровня поля (или эквипотенциальная поверхность) — это геометрическое положение точки в пространстве, где полевая функция u = * F (x, y, r) имеет то же значение C.
Форма уравнения горизонтальной плоскости F (x, y, r) -C. Придание C различных значений дает нам семейство поверхностей уровня. Например, если поле задается функцией u = * xr — \ — yi — \ — z ‘\, поверхность уровня является сферой x2-t- * / 2 + z2 = C По центру в начале координат. Если скалярное поле является полем распределения температуры в определенной части пространства, горизонтальная плоскость Это так называемая изотермическая поверхность, то есть поверхность с постоянной температурой. В дополнение к скалярным полям в пространстве, плоские скалярные поля также рассматриваются.
Плоское скалярное поле определяется как часть плоскости (или всей плоскости), каждая точка P которой соответствует числовому значению для скалярной величины z. Функция плоского скалярного поля зависит от двух переменных: z = f (x, y). Рисунок 221
Этот случай можно свести к предыдущему, написав уравнение (55) в следующем формате: И положить тогда z) = -f’x (x, y), //, 2) = -f’u (xt y), t /, r) = 1 Таким образом, grad Z7 (* 0, // 0, zv) = F’x (x0, y0Y z0) \ — \ — F’y (x0t y0, z0) j + F’z (xot y0, z0) k = — / iC * o, U.) Yo) —1y (Ho, Yo) 1 Нормальный единичный вектор n в этом случае Мулы n = -fx (* ot Yo) ‘-fy (* o> Yo) i + k ^ V1 + f’ * (x0, Yo) + Gu (* 0. Yo) И его индукция косинус — по формуле cosa = .YYx {X * Y ° 1 ‘cosp = -Yy (* «‘ Yo \ r V Yo) K 1 + / * (* o> Yo) H- / ^ (* o.Yo) cos 7 = -y — 1-. (60)
Пример 2. Найти уравнение касательной плоскости эллиптического параболоида z = x2 в точке P0 (1; -2; 3). Решения. Если вы введете -f ~~ = / (x, y), вы получите f’x (x, * /) = 2x. GAC> Y) = Y, поэтому f; (1, -2) = 2; /; (1, -2) = -2. Теперь используйте уравнение (57), чтобы легко получить уравнение касательной плоскости. 2-3 = 2 (х-1) -2 (г / 4-2), или 2x — 2y — r — 3 = 0.
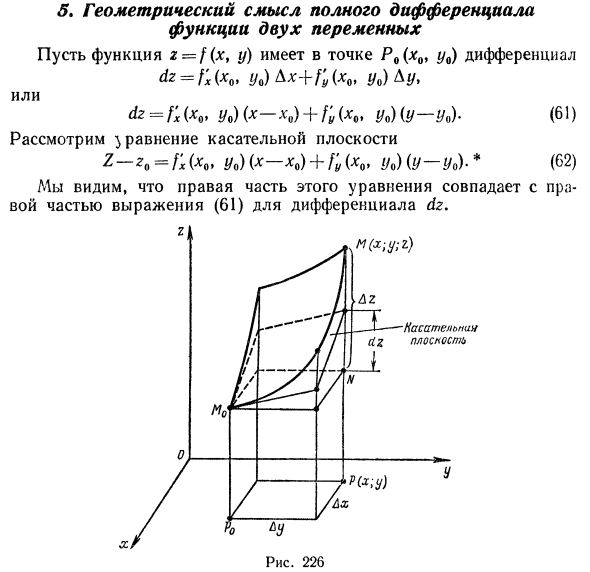
<5. Геометрический смысл полной производной функции двух переменных Предположим, что функция z = f (xt y) имеет производную в точке P0 (x0, y0) dz = /; (x0, y0) Ax + f’y (x0, y0) Ay, или dz = f’x (x0, y0) (x-x0) — + fy (x0t y0) (у-у / о) (61) Рассмотрим уравнение касательной плоскости Z — z0 = f’x (x0, y0) (x — x0) + [y (x0, y0) {y — yo) — * (62) Вы можете видеть, что правая часть этого уравнения соответствует правой части дифференциального уравнения dz (61).
В результате левые части этих уравнений равны, но в уравнении (61) левая часть является производной функции z = f (x, y) в точке P0 (xQy y0) и уравнения (62) В, левая сторона означает соответствующее приращение касательной плоскости Сделан следующий вывод, объясняющий геометрический смысл производной функции двух переменных. Производная функции двух переменных равна соответствующему приращению приложения касательной плоскости (см. Рис. 226).
Плоские скалярные поля представлены геометрически с использованием линий уровня. Линия уровня определяется как геометрическое положение точки на плоскости, у которых плоские скалярные функции поля имеют одинаковое значение. Функция z — для плоского скалярного поля f (xy y) уравнение линии уровня имеет вид f (x, y) = C, Где С является константой. Например, для плоского скалярного поля, определяемого функцией r = x2 — y%, линия уровня является равносторонней гиперболой xg — yy = C (рис. 221). Если 0, получите x2 — y2 ^ 0 или (* — y) (x + y) = 0. Это означает, что асимптоты гиперболы x-y = 0 и x + y = 0 (биссектриса угловых координат) также находятся на линии уровня рассматриваемого поля.
Производная направления Предположим, что задана дифференцируемая функция скалярного поля u = F (x, y, r). Рассмотрим точку P (x \ y, z) и ray / в этом поле, оставьте точку P в направлении единичного вектора I = cosa • i -f- cosr • j + cosу • k, Где a, p и y — углы между вектором I и осями координат. Пусть P1 (x + ^ x; y — * — y, 2 + D2) — другая точка этого луча. Разница между значением функции и скалярным полем в точках P1 и P называется приращением направления I функции и обозначается как Atu. тогда klu = F (x + A *, y — \ — Ay, 2-bA2) -F (x, y, z) Он также показывает расстояние между точками A / P и Px: A / = PP1. Производная функции u = F (x, y, z) в направлении определения I является предельным пределом. D / -0A / Производная функции u по направлению / обозначена символом ^. Вот так Отметим, что> 0, если производная функции u в точке P (x \ y \ z) в этом направлении / положительна.
Когда направление увеличивается ~~ 0, затем функция Направление / уменьшение. Мы можем сказать это ди направленность Указывает скорость изменения функции в этом направлении. Выведите уравнение для вычисления производной по направлению. Во-первых, обратите внимание, что приращения координат Da, Dy и D2 точки P связаны с длиной сегмента PXP = D /. К косинусу вектора I (рис. 222) при следующем соотношении: D; c = D / cosa; D * / = D / старение; Dg-D / cos-y. (38) Поскольку функции и гипотезы дифференцируемы, приращение Dm в точке P (x \ y \ z) можно выразить в виде Di = F’x (xt yt z) Ax + (x, y, z) Dy + F’z (x, y, z) Az + o), (39) в Рисунок 222
Кроме того, o) стремится к нулю быстрее, чем p- \ / Dl’2 + Ar / ‘2 + Ar’ ^. lim— = 0 (см. § 4, параграф 2, уравнение (19)). р-0 С учетом приращения функции вдоль луча в направлении вектора I Au = A, n, p = A /, а Ax, A y и Ar выражаются уравнением (38). Таким образом, уравнение (39) принимает вид: Atu = F’x (xty, z) A / cos a + F’y (x, y, z) A / cos (5-f (x, y, z) A / cos y + co. Разделив обе части этого равенства на AI и передав его до предела как A / — * 0, получим: lim lini [F’x (x, 2) cos a-f- / 7; ^, y, z) cosfi-f- 01 Д / -0 Вт Д / — ♦ • о + / 7; (a: (z) cos 7] — {- lim ~. Ho F’x (xty, z), F’y (x, y, z), F’z (xty, z) и направляющий косинус A зависит от / и lim lim- = 0, поэтому О С-р-о Р ^ = (X, y, z) cos a + Y7; (x, z) cos p + F \ (xt y, z) cos (40)
Из уравнения (40), если вектор I соответствует одному из единичных векторов i, j или k, производная и направление / соответствуют соответствующей частной производной этой функции. Так, например, если l = i, cosa = l, cos (5-0, cosv = 0, так ^ = F’x (x, y, r). Пример Найти производную функции u = xr — 2xz + y2 в K точках Pl в направлении от Px (1; 2; -1) P (2; 4; -3). _ Решения. Вектор PXP2 = (2-1) найден! -f (4-2) j -f — (- 3-f-l) k = i-f2j-2k и соответствующий единичный вектор »KPl _ i + 2j-2k 1 _2 2. 3 часа
Таким образом, вектор I имеет следующее направление косинус. 1 2 2 cos a = -y; cos p = y; cos y = -. Теперь мы нашли частные производные функции u-x2-2 * 2-f — {/ : §;. = ( ‘-2×2 + y *); = 2x-22; d £ = -2×2 + g / 2); = 2 //; Сделать Значение в точке P1 (1; 2; -1): , ди * = 1 = 4; -7- г -1 -1 до UM = (2 </) = (21 — 22) -4 • — = -2, г LH = 1
Подставляя значение частной производной, найденной в уравнении (40), и определяя косинус, получается искомая производная. £ = 4. ± -4.4 + (-2) (-4b Если скалярное поле плоское, как уже упоминалось, функция поля r зависит от двух переменных: z = f (xt y). В этом случае вектор I находится в плоскости Oxu (то есть cos 7-0) и, следовательно, Y. Следовательно, поскольку I = cosa-i-fcosp-j или I-cosa-i + sin aj, cos p == sina (фиг. 223). Формат уравнения дифференцирования (40) для плоского скалярного поля: = fy (X ‘Y) = TG2y Значение в точке P FX (I; 2) -1-2; 2) ~ = 1 1 + 2-А 1 + 2 Чтобы найти коса и грех в уравнении (41), найдите угловой коэффициент касательной в точке P (1; 2).
Так что tga = 1 и получим два значения a. а «45 ° и -225 °» соответствуют двум противоположным направлениям касательной. V 2 V ^ Для ax = 45 °, cos ax = cos 45 ° = ^ y- \ sin a-sin 45 ° ~. Следовательно, формула (41) sc_ 1 V2 || / «2 _ 3 \ G2 a / ‘2 2 +1’ 2 4 ‘ n ooso di 3 / «2 Если ar = 225 °, -m =-получается тем же способом.
