Сверхзвуковые конические течения. Некоторые точные (нелинейные) решения

Сверхзвуковые конические течения. Некоторые точные (нелинейные) решения

Сверхзвуковые конические течения. Некоторые точные (нелинейные) решения. Представьте себе конус с вершиной в начале координат и произвольной направляющей, окруженный сверхзвуковым потоком сжимаемых жидкостей. Предположим, наше тело имеет такую форму, что оно расположено в таком образе по отношению к потоку, и скорость потока оказывается в форме.

Где vx, v2 меньше vv, а его квадрат равен Игнорировать, как и предыдущий метод Пункты. Вопрос такой шаг был исследован Буземана!). Как и раньше, вы можете написать о возможности скорости. В общем, х1 !Е| Плоскость (;, 17) может дать простой геометрический смысл.

Обтекание прямого круглого конуса так же, как и обтекание края плоского прямоугольного крыла, являются частными случаями более общей задачи обтекания произвольного конического тела. Людмила Фирмаль

Это плоскость, которая параллельна плоскости (*, y) и находится на расстоянии 2 = 1 от[2 = 1 (31 .2) ] от конца . Легко проверить, что уравнение (31 .3) имеет смешанный тип .Часть плоскости ( , m}) представляет собой эллипс, а другая — hyperbola .In дело в том, что в соответствии с характеристиками, если искать последнее уравнение в виде = 17 (5;), то оно есть.

Смотрите также:

Примеры решения по гидромеханике

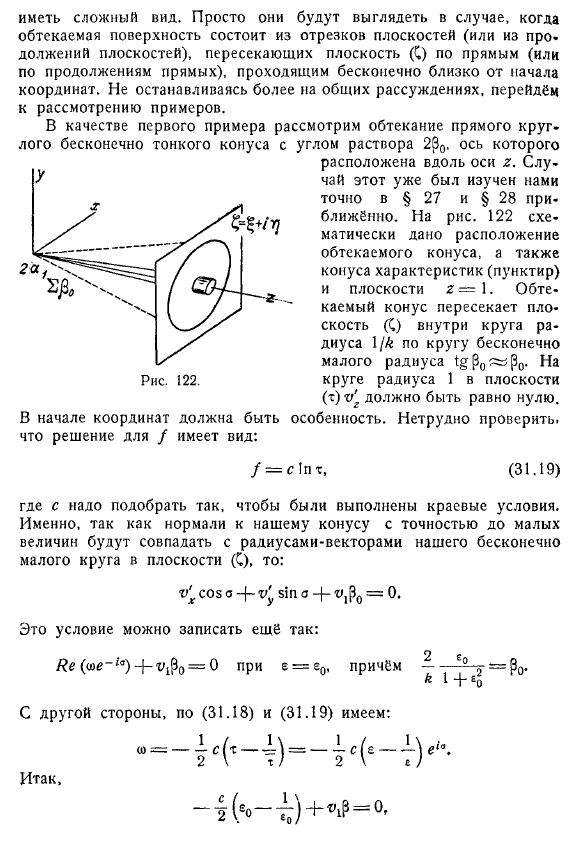
Таким образом, в пределах окружности с радиусом 1 / k уравнение (31 .3) является эллиптическим .Напротив, для k2 + r) 2> 1) k2, вне окружности радиуса l / k, существуют реальные характеристики .Последние представлены в виде всевозможных прямых линий, касательных к окружности с радиусом 1 / &1) .Рис . 121 приведены некоторые Эти характеристики (1 семейство-сплошная линия, еще 1 семейство-пунктирная линия).

Смотрите также:

1. Сверхзвуковое обтекание тонкого крыла конечного размаха произвольной формы в плане. Концевой эффект н вихревая пелена.

Окружность радиуса l / k в плоскости ( m ), является точкой пересечения плоскости конуса характеристики в пространстве по (31 .4) = 1, y, 2) .Обтекаемое тело пересекает плоскость (*, **) вдоль определенной кривой .Эта кривая полностью находится внутри окружности радиуса 1 / k, или полностью вне этой окружности, или, наконец, частично внутри, частично снаружи .После того, как вы описали граничные условия, вы должны приступить к решению (31 .3).

Смотрите также:

1. Осесимметричное обтекание с отошедшей ударной волной.

С геометрическим преобразованием переменных, заимствованным из того же исследования Чаплыгина, Буземан сводит (31 .3) к 2-мерному уравнению Лапласа 2) .Это просто для уравнения Лапласа >) Проще всего проверить это, если перейти к полярным координатам r, в плоскости полярных координат e (радиус-вектор) и o (полярный угол).

Плоские безвихревые движения, которые мы изучали ранее, являются частным случаем рассматриваемых сейчас движений. они получатся в случае, когда кривая l — плоская кривая. Людмила Фирмаль

• Поэтому можно рассматривать v *как вещественную часть функции комплексной переменной х = ee19. (31. 10 Буква 5 обозначает мнимую часть этой функции и пишет / + * =]（31. 11 Легко видеть, что внутренняя часть окружности с радиусом 1 / k плоскости ($, m/) проходит через плоскость (m) внутрь окружности с радиусом 1 (e = 1). На самом деле. 4. Поэтому, когда r изменяется от 0 до 1, он изменяется от 0 до 1 / k. =является полярным углом в преобразовании не менять.

Прежде чем уточнять граничные условия плоскости (m), посмотрим, как скорости m, r выражаются в функции новых переменных e и o. Найти полную разность при движении вдоль радиус-вектора. Вы можете вспомнить его в r. Это потому, что нет никакого вихря. Кроме того, вы можете легко выразить правую часть этого уравнения в терминах функций (сопряженных с).