Оглавление:










Теория пограничного слоя. Точные решения для одновременного переноса тепла, массы и количества движения
- Решение вышеуказанных задач методом пограничного слоя ранее основывалось на карманных интегральных соотношениях (4.125), (11.100) и (18.76). Они получены интегрированием уравнений пограничного слоя Прандтля по координате y. To решая уравнение Калмана для толщины пограничного слоя 6, 6, 6С, необходимо указать форму профилей скорости, температуры и концентрации. В этом разделе представлен более строгий метод точного решения уравнений пограничного слоя Каталитически [17]. Прандтля*; этот метод лучше иллюстрирует детали механизма передачи.
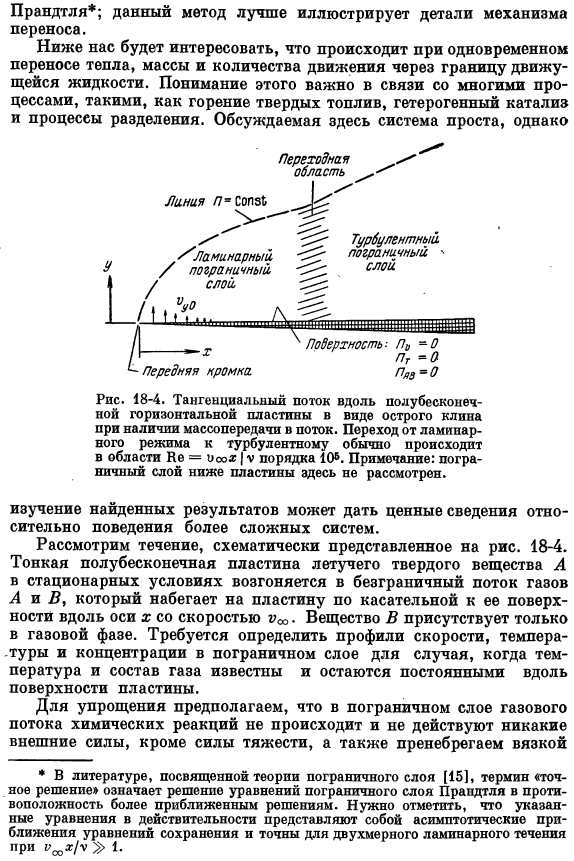
Ниже вас заинтересует, что происходит, когда тепло, масса и импульс движутся одновременно через границы движущейся жидкости. Понимание этого важно в связи со многими процессами, такими, как сжигание твердого топлива, гетерогенные катализаторы, процессов разделения и т. д. Описанная здесь система проста、 18-4.Тангенциальное течение вдоль полубесконечной горизонтальной пластины в виде острого клина при наличии переноса ионов в поток. Переход от ламинарного течения к турбулентному обычно происходит в области»Re = Ueo»|. v составляет около 10 секунд. Примечание: пограничный слой под пластиной здесь не рассматривается.
Поверхность 3—4 смещена с поверхности стенки на сторо1не входа охладителя на такую величину, что она находится снаружи пограничного слоя, который лежит с этой стороны стенки. Людмила Фирмаль
Изучив найденные результаты, можно получить ценную информацию о работе более сложных систем. Рассмотрим поток, схематично изображенный на рисунке. 18-4.In стационарное состояние, тонкая полубесконечная пластина Летучего твердого вещества а сублимируется в неограниченный поток газов а и B. It течет по пластине со скоростью VCO тангенциально к поверхности на пластине. Если температура и состав газов известны и остаются постоянными вдоль поверхности пластины, то необходимо определить скорость, температуру и концентрационный профиль пограничного слоя.
Для простоты предположим, что химические реакции не происходят в пограничном слое газового потока, что внешние силы не действуют вне гравитации и что они игнорируют вязкость. Рассеивание, смешанное тепло, поглощение лучистой энергии. Эти предположения оправданы для большинства скоростей потока газа. Кроме того, для газовых смесей, р*, р, Ср, X, С, и DAB используются в качестве констант.* Непрерывные уравнения Уравнение движения Уравнение энергии (18.91) Уравнение непрерывности материи в (18.94) г = 0 Условия обучения-это соотношение: Последнее уравнение основано на предположениях, оно существует только в газовой фазе и никакой химической реакции не происходит.
Мы можем интегрировать уравнение непрерывности . Где индекс » O » указывает на условие y = 0.2-е отношение получено из выражений (k) и (y) в таблице. 15.3. Согласно определению СПАО, основанному на законе Фика (15.16), мы можем видеть, что: («Ло + ^ во) Замените формулу NB₀ из Формулы (18.101) на Формулу (18.104) и сравните результат с формулой (18.103). ML eDAB SxA I C dv、 Р•>,| » Дж..»» эту формулу для vy следует использовать в уравнении (18.92)-(18.94).Ранее предполагалось, что MA = Mv, поэтому можно задать значение MAc / p = 1 -. Определение безразмерного профиля в качестве выражения (18.106) (18407) (18408) Вводится безразмерная зависимость физико-химических свойств среды.
Даны новые обозначения, обобщены уравнения движения, энергии и непрерывности вещества а Кроме того, граничные условия для r> x, T и xA принимают следующий вид: pr = 50 или p = oo = = 1(18.113) если y = 0, то P = 0(18.114) Форма граничных условий безразмерного профиля Р и отсутствие линейной размерной характеристики течения позволяют предположить, что может быть использована переменная подстановка. На основе уравнения (4.122) строится безразмерная комбинация переменных вида: Если мы представим производную выражения (18.112) с q, то получим*.
Ил- Из этой зависимости видно, что скорость массопереноса вблизи стенки, представленная через градиент концентрации Pl(0), непосредственно влияет на все 3 профиля: Po, Pu и поверхностно-активное вещество.
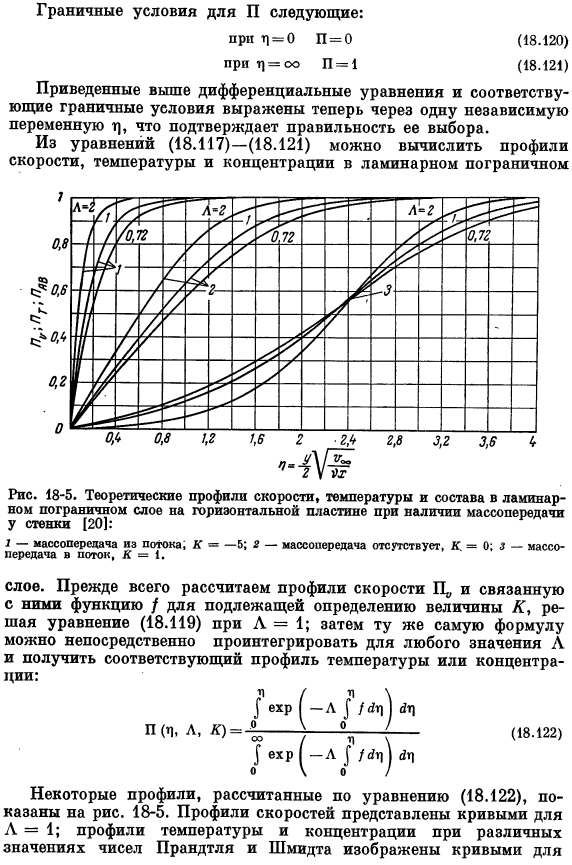
Для удобства последующих вычислений введем следующие обозначения: / = — £ + } 2nvdn (18.117) Значение K представляет собой безразмерный массовый расход стенки, определяемый следующим уравнением (18.118) Для ламинарных пограничных слоев остаются постоянными**.Уравнениями движения, энергии и непрерывности в приближении пограничного слоя являются: — А / П ’ = П » (18.119) — Х «» 1 2.— дз- | З-О Этот раздел представляет собой поверхностно-активное вещество l nAB KhAB K-это (18.118 в) Граничные условия для P следующие: если d = 0, то P = 0 (18.120) ч = ОО П = 1(18.121) Приведенные выше дифференциальные уравнения соответствуют Слой.
Сначала вычислите профиль скорости Щ и связанную с ним функцию/и решите уравнение Л= 1 (18.119) для определяемой величины K. Затем вы можете напрямую интегрировать одно и то же уравнение в любое значение A, чтобы получить соответствующий температурный профиль или концентрацию (18.122) На рисунке показаны несколько профилей, рассчитанных по формуле (18.122). 18-5.Профиль скорости представлен кривой с a = 1.Профили температуры и концентрации различных значений чисел Прандтля и Шмидта являются、 Соответствующее значение L.
Гидродинамические, температурные и диффузионные пограничные слои становятся толстыми, когда безразмерная скорость массопереноса K положительна (например, испарение), и тонкими, когда отрицательна (например, конденсация). Безразмерный наклон скорости, температуры и концентрации вблизи стенки P ’(O, A, K) определяется по производной формулы (18.122). (18.123) В таблице представлен обзор значений, вычисленных в этой формуле путем численного интегрирования. 18-3. Давать определение Поток импульса, энергии и массы называется безразмерным выражением gglii-o_1Г(0, Лг, я) (ro -?2LT (18.124) (18.125) И табличные значения P ’(O, L, K).
- Таким образом, мы можем рассчитать вышеупомянутый поток через безразмерную скорость массопереноса K. Определение скорости массопереноса как функции заднего и xa показано в Примере 18-6. В некоторых ограниченных случаях профиль Pr и Pav можно найти аналитически. Например, при высокой скорости массопереноса K и большом значении Lt (число Прандтля) или Ldv(число Шмидта) температурный или диффузионный пограничный слой значительно тоньше гидродинамического пограничного слоя, и для получения полного решения температурного профиля необходим только градиент скорости стенки. И концентрация P(c, L, K).
Как показано ниже, если A большое, то небольшие изменения в K значительно повлияют на профиль температуры и концентрации. При низкой скорости массопереноса(| K | профиль скорости вблизи стенки принимает следующий вид: (18.127) При описании этой формулы использовались значения скоростей d = 0 и K = 0(см. табл. 18-3).Затем вы можете использовать выражения (18.117) и (18.122), чтобы получить*для меньших значений K и a> 1. Джей ехр (ЛРК — 1,328 ЛД » / 31) П(18.128) Ф ехр (ЛРК-1.328 ЛД » / 31) Согласно формуле (18.123), соответствующий температурный или концентрационный градиент стенки равен[20, 26].
Температура, которую принимает неподвижная стенка со стороны потока газа, может быть получена при помощи теплового баланса на контрольном объеме, как показано на рис. Людмила Фирмаль
В следующих разделах обсуждаются безразмерные профили и градиенты для малой массовой скорости перемещения K. С ограничением k — * ■0 профиль выглядит следующим образом: Джей ехр(-1.328 ЛД> / 31) ДД Лира P(1), L, X)»——————(18.130) к * °Щ ехр(-1. 328Lt3 / 3 |)л] г(т»»)» Лим П (Д, т, K)=(18.131) «(!) ■°) (18.132) Γ (x, y) — неполная Гамма-функция[27] *. Этот профиль показан на рисунке. 18-6; обратите внимание, что это примерно та же форма, что и конечные значения фигур A и K = O профилей. 18-5.Используя формулу (18.129), найдите наклон профиля вблизи стены.
Уравнение Л= 2 (18.133) дает отклонение от данных, полученных при применении полного профиля скорости. Это всего лишь 1%. — Для*°°, Матч будет завершен. Подробное сравнение приведено в таблице. 18-4. Профиль Таблица 18-4.По сравнению с незначительным * Расчетное значение P ’(0, d, 0) точный. resolutionП ’(0,Л, 0)-0,в774д‘ / «П-(оГд, 0)-0,ВВ4д?/> 0.6 0.552 0.571 0.560 0.8 0.614 0.629 0.616 1.0 0.664 0.677 0.664 2.0 0.845 0.853 0.837 7.0 1.296 1.29 1.27 10.0 1.459 1.46 1.43 15.0 1.671 1.67 1.64 Кроме того, указывается Расчет уравнения Р ’ (О, Л, 0)»₃0.
Предложенная порхаузеном[23] для приближенного объяснения вычисленного значения погрешность до а = 0,6 приводит к хорошему результату в пределах±2%.Назначение приближенных уравнений полхаузена уравнениям(18.86) и (18.87) * Функция Г (х, оо)-г (г)-полная гамма-функция. Удобное соотношение может быть получено при низкой скорости массопереноса Р»»*⁰.(ТТ)») Здесь Ре = В / В. Формула (18.135) подтверждает справедливость подобия потока Чилтона-Колборна (см. разделы 13.2 и 20.2), принимая во внимание значение Pr или Sc.
Для расширения найденного аналитического решения до несколько более высокой скорости массопереноса необходимо последовательно расширить exp (Ayl|) и определить профиль из уравнения (18.128) в последующих терминах интегралов. решение Лу-это (18.137) Раньше, u = 1,328 Lts / 3!, Параметр-безразмерная скорость передачи КЛ Р ’ (0, Л, 0) Уравнение для больших Λ С учетом уравнения(18.133) — Это! Г Коэффициент С можно рассчитать по формуле: ?(■ На рисунке показаны несколько профилей, рассчитанных по формуле (18.136). 18-6.Показанный профиль похож на профиль, показанный на рисунке.
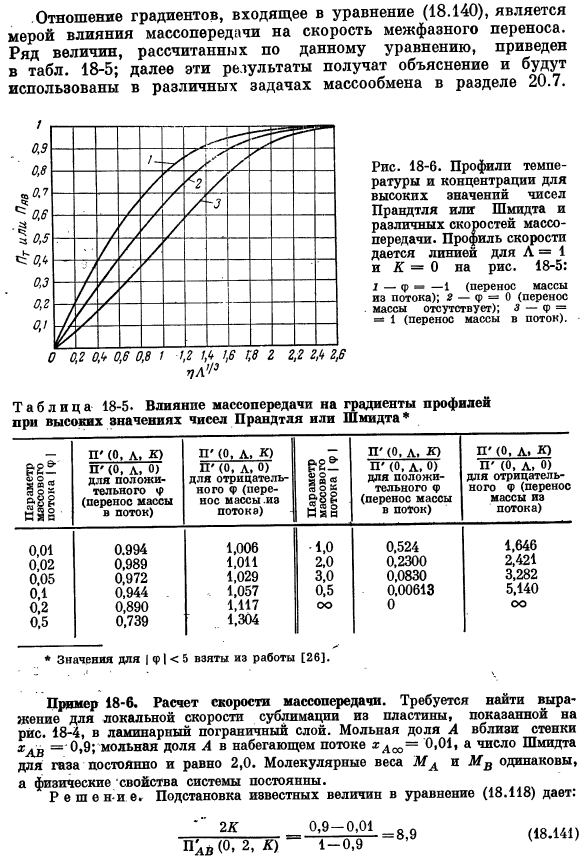
И изменяются с изменением скорости массопереноса. Заметим, что параметр, определяющий форму профиля, будет очень большим, несмотря на ограничение, накладываемое профилем K, поскольку значение параметра A предполагается большим[см. формулу (18.138)].Наклон этих профилей на стене описывается формулой[20, 26). (18.139) (18.140) Коэффициент градиента, содержащийся в уравнении (18.140), является мерой влияния массопереноса на скорость межфазного движения.
В таблице приведены многие значения, рассчитанные по этой формуле. 18-5; далее эти результаты обсуждаются и используются в разделе 20.7, посвященном различным вопросам массопереноса. 0-Д ’(0,Л, К)Д’(0,Л, К)Привет Д ’(0.Л, У) Ну дмотоитсатей — | / / (мама Кэрри 0.01 0.994 1.006 −1.0 0.524 1.646 O. O2 0.989 1.011 2.0 0.2300 2.421 0.05 −0.972 1.029 3.0 0.0830 0.1 0.944 1.057 0.5 0.00613 5.140 0.2 0.890 1.117 0 0.5 0.739 1.304 Пример 18-6 расчет скорости массопереноса. Из приведенной на рисунке пластины необходимо найти формулу локальной скорости сублимации. 18-4, к ламинарному пограничному слою.
Молярная доля а вблизи стенки ГДД = 0,9; молярная доля а в набегающем потоке ксако= 0,01, число Шмидта газа постоянно и равно 2,0. Молекулярная масса Ма и МВ одинакова. Решение n-е. подставляя известную величину в выражение (18.118), получаем: 2К Пав(0, 2, К) (18.141) Как решить эту проблему Соотношение приведено в таблице. 18-3.
Смотрите также:
| Нестационарная диффузия | Распределения концентраций в турбулентном потоке |
| Теория пограничного слоя. Приближенный метод Кармана | Осреднение уравнения неразрывности для одного компонента по времени |
