Оглавление:













Устойчивость равновесия системы
- Равновесие материальной точечной системы называется устойчивым, если система последующего движения почти не отклоняется от рассматриваемого положения равновесия, после чего точке системы сигнализируется очень малое начальное отклонение и очень малая начальная скорость от положения равновесия. Посвящена исследованию голономной, установившейся и равновесной устойчивости системы при условии идеальных связей. Если такая система находится в консервативном силовом поле, то устойчивость равновесия системы определяется в соответствии с теоремой Лагранжа Дирихле или теоремой Ляпунова.
Вот теорема Лагранжа-Дирихле если потенциальная энергия минимальна в изолированном положении равновесия системы, то положение равновесия устойчиво. Потенциальная энергия системы может быть разбита на ряд степеней обобщенных координат. Разложение начинается с члена 2 или более для координаты, если положение равновесия является началом координат и потенциальная энергия в положении равновесия считается равной нулю. Если в положении равновесия потенциальная энергия не минимальна, то для определения устойчивости равновесия необходимо применить теорему Ляпунова.
Материальную точку следует изображать в промежуточном ноложепии, соответствующем положительным координатам этой точки, и предположить, что точка движется в сторону возрастания этих координат. Людмила Фирмаль
А если отсутствие минимума потенциальной энергии можно определить в члене 2-го порядка 1 расширения потенциальной энергии, то без учета членов более высокого порядка равновесие системы неустойчиво. Б если энергия положения максимизируется в положении равновесия, то равновесие системы становится неустойчивым. Обновление 1 соображений самого низкого порядка, фактически доступных в серии расширений потенциальной энергии. Вторая производная потенциальной энергии, рассчитанная в положении равновесия Коэффициент c является постоянной величиной. Выражение потенциальной энергии 1 принимает вид П у ss 1 4- 99п 2cu Ифт 2sya 1 1Н 1chn 3 Здесь точка обозначает член более высокого порядка для qu.
В квадратичной форме н — г — КК СП л 2 syaLn-1Yal 4 Определенно положительный qb .. Суммарная потенциальная энергия, определенная в Формуле 3, ft, которая одновременно положительна для всех значений qn и не равна нулю одновременно. .положительный для достаточно малого значения qn .Это означает, что равновесие потенциальной энергии будет минимальным. Согласно теореме Лагранжа-Дирихле, в этом случае положение равновесия устойчиво. Создайте матрицу коэффициентов c y SC SC С1Я смотрите Си. КТОС.5 По равенству 2 с 9.То есть матрица 5 симметрична. Вычислите минор 5 главной диагонали матрицы. СС 1sy .. Улыбка Д1 а, д, ,. Д. .. ..
Технические характеристики КИУ В высшей алгебре доказываются следующие критерии Сильвестра вся главная диагональ матрицы 5 минор дъд2,. .Если, Дя положительно Д1 0, Д4 0, .D 0, 7 Квадратичная форма 4 определенно positive .At меньше всего. Если 1 из главных диагональных миноров отрицателен, то 2-я Форма 4 может принимать отрицательное значение. Из теоремы Лагранжа Дирихле видно, что при выполнении условия Сильвестра 7 положение равновесия консервативной системы стабилизируется. Если хотя бы 1 неравенство 7 имеет противоположное значение, то на основании первой теоремы Ляпунова положение равновесия становится неустойчивым.
Для систем С 1 степенью свободы, критерий устойчивости принимает очень простую форму.3 p 0 стабильное равновесие, d o o неустойчивое равновесие.8 Этот критерий указывает на то, что равновесие является устойчивым или неустойчивым, если смещение системы бесконечно мало Из положения равновесия энергия положения увеличивается или уменьшается соответственно. Для наглядности приведем диаграмму. 18.1 потенциальная энергия гравитации. При решении задачи об устойчивости равновесия системы с 1 степенью свободы под действием потенциальных сил рекомендуется следующая процедура.1 Выбрать систему тела или тело, в котором рассматривается равновесие, и обобщенные координаты.
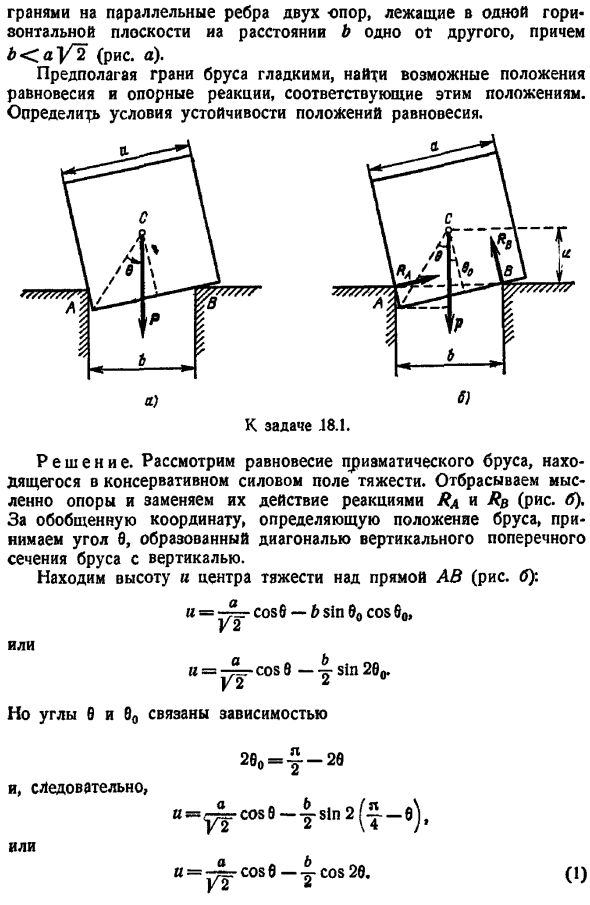
Его задача определяет местоположение системы.2 выразить потенциальную энергию системы 3 найти возможное положение равновесия системы путем вычисления производной потенциальной энергии системы относительно обобщенных координат и приравнивания ее к нулю.4 для каждого из возможных положений равновесия, рассчитав значение 2-й производной потенциальной энергии относительно обобщенных координат, найти знак этой производной и определить по ним ее устойчивость. Задача 18.1.Однородная призменная балка с квадратным поперечным сечением массой p, стороны которой равны a, опирается на свою сторону. На расстоянии b друг от друга до краев 1 2 пор на одной горизонтальной поверхности оно равно b ay2 рис. а.
Предполагая, что края пучка гладкие, находим возможные положения равновесия и вспомогательные реакции, соответствующие этим положениям. Определите условие устойчивости положения равновесия. Проблема в j8.1. Решение. Рассмотрим равновесие призменного пучка, который находится в поле действия консервативных сил гравитации.
Мысленно отвергните опору и замените действие реакцией ra и rb рисунок b. Для обобщенных координат, определяющих положение балки, возьмем угол 8, который образуется диагональю вертикального сечения вертикальной балки. Найдите высоту и центр тяжести над прямой ab рисунок b Но углы 6 и 80 связаны Следовательно, или 280 y-28 И cos 8-cos 28 случай.1 Потенциальная энергия гравитации Когда дано yl-p-u, 1 Найдите производную по p 6 и уравняйте ее с нулем. Из этого уравнения мы видим, что возможны 2 положения равновесия. Первое положение равновесия будет sin 9 0 или 6 0.2-е равновесие Или Такое положение равновесия возможно в следующих случаях Здесь мы находим 2-ю производную.
Для решения задачи устойчивости равновесия необходимо найти знак этой производной для каждого из возможных равновесий positions .In первая позиция, 8 01 0. Если присвоить это значение выражению 3 Таким образом, по теореме Лагранжа-Дирихле это положение равновесия стабилизируется в следующих случаях Б В противном случае положение равновесия неустойчиво.2-е положение равновесия 8 8, arccos y . Подставляя это значение для угла уравнения 3 Но согласно 2 Так.. 1 о b4 — 2В 0. 1 РФ п р А. Е. То есть положение равновесия fl fls по теореме Ляпунова неустойчиво. Исключение составляет 0 0 и — —2В 0 Это соответствует первому положению равновесия, рассмотренному ранее.
Возможные положения равновесия твердых тел могут быть определены другим способом. Создайте 3 уравнения равновесия для любого положения луча Рис. 5, определяемого углом 0. Первое уравнение-это равенство суммы проекций всех сил на горизонтальную ось нулю. Потому что fl0-РБ РА греха fl0 0. 4 2-е уравнение-это равенство суммы проекций всех sls на вертикальную ось нулю. РА греха 9е потому что fl0-П РБ 0. 5 3-е уравнение-это уравнение к нулю суммы момента силы относительно точки А rb b cos fl0-p sin 9 b sin 90 0.
Из формул 4 и 5 РБ Р потому что 90 Подставляя это значение в уравнение 6, можно найти следующее pb cos 90-p — sin in b sin fl, j О пожелать 2fl0-ДГ грех 9 0 0 П2 bcos2-c — sin 9 0 b грех 29-ДГ грех 9 0 2 И наконец sinfl 2bcosfl — — 0 Вот значение угла b, которое соответствует 2 возможным положениям равновесия 1 sin8 0, следовательно, 8 61 0. 2 cos, следовательно 0 8a arccos. Первое решение соответствует симметричному положению луча. Град балки наклонен под углом 45 к горизонтали. Для 2b r2 возможно 2-е решение. Если a 2bpr2, то мы находим cos8a 1, то есть sin 6a 0, и возвращаемся к первому случаю.
Найти величину реакции в первом возможном положении равновесия 2-е положение равновесия Р Д Т 4b2-а 8б ч п РБ а Фольксваген П. И 1л Если мы сравним оба решения, то в первом методе мы увидим, что можем непосредственно определить характер возможных положений равновесия системы и устойчивость этих положений равновесия. Однако этот метод не находит ответа поддержки. 2-й способ позволяет непосредственно определить возможное равновесное положение системы и соответствующую реакцию носителя, но не дает оценки устойчивости равновесия системы и характера устойчивости этих равновесных положений.
- Конечно, после использования этого метода для определения реакции и положения равновесия необходимо вернуться к теореме Лагранжа-Дирихле, чтобы ответить на вопрос об устойчивости равновесия. Задача 18. 2. 2 палочки Каждое соединение длины i и веса q соединено точкой a. 1 одним из стержней является задача 18. 2. Зафиксированный в точке o, конец 2-го b находится на гладкой горизонтали floor. At в точке b сила p постоянной абсолютной величины приложена горизонтально, и в положении равновесия стержень oa образует вертикальную линию и угол a, а стержень ab образует горизонтальную линию и угол p. Определяют устойчивость равновесной системы. Решение.
Рассмотрим равновесие системы, состоящей из od и as стержня. Выберите угол 0 для обобщенных координат, определяющих местоположение системы. Начало координат выбирается в точке b, которая является пересечением вертикальной и горизонтальной плоскостей, проходящих через точку o. Ось x направлена влево, а ось 2-вверх. 3 активные силы qx q действуют на систему и r. Потенциальная энергия системы 0 Р1 Р Пх 1 Где zi, zt и x-соответствующие координаты точек ci, c и b.
Зная относительное движение материальной точки, можно непосредственно найти уравнения переносного движения подвижной среды. Людмила Фирмаль
Представлены обобщенной координатой 0. 2 i — ysin0, 2 sin 0 y cos a, x z cos0-later. На рисунке показана зависимость между углом a и 0. Я потому что грех 0 футов. Где ft-расстояние между точками o и bq. Из последнего равенства Выражение для потенциальной энергии теперь можно свести к этой форме пренебрежимо малая константа — z отбрасывается p qi sin 0 pl cos0-sin a. 3 Отсюда — Ци cos0-ЛП грех 0 потому что г Или, учитывая значение ba d0 из 2 cos0 КЗ-ПЗ грех 0 cos0ctg а.
Если вы уравняете dn b0 до нуля, вы найдете равновесное состояние системы q tg0 ctga p. 5 4 рассмотрим дифференцирование и приобретение относительно 0 — Ци Син 0-ЛП потому что 0-0 грех ктг а —. Если я использую 5 из этого выражения, чтобы удалить значение q Потому что грех в02 Р А Ж Согласно 8, для b n dr 0 равновесие является устойчивым. Грех потому что p, или Сова г-а б. Это приводит к состоянию А Р. 7 При выполнении условия 7 равновесие системы стабилизируется. Это условие соответствует положению точки b слева от точки r.
Действительно, если точка b совпадает с точкой bn йа Р Вы можете видеть, что равновесие устойчиво, если точка b находится слева от cc, и неустойчиво, если точка b находится справа от b0. Задача 18л. Однородный стержень ОА массой Р и длиной 21 опирается на стержень БК, который закреплен на конце шарнира О и в точке в закреплен на центральной части шарнира ОП. Стержень массой Р и длиной 21 в точке БК с. Расстояние ООТ l. Определить возможное положение и устойчивость равновесия системы. Solution. It представляет собой потенциальную энергию системы, состоящей из стержня ОА и bc. In обобщенные координаты, выбираем угол p.
Социальная энергия системы, образованной стержнем, представляется следующей формулой p — pz cos -q zcos 180 −2 p или П — pl cosф-q z-i cos2ф. Чтобы определить возможное положение равновесия, найдите производную потенциальной энергии относительно обобщенных координат. ПЗ sinф-2qzsin2ф И тогда мы приравниваем его к нулю. Pzsin −2qz 2 sin cos 0. К заданию 18. 3. В веотикал.
Горшок Заметим, что q 2r, находим из последнего уравнения sin f 1-8cos p 0 Итак, если sinq 0 или cos 1 8, то есть равновесие возможно при 2 значениях угла. 1 Ф1 0 и 2 arc arccos 82 48. Чтобы определить устойчивость каждой из этих позиций, найдите производную 2-го порядка потенциальной энергии относительно обобщенных координат. ЛП с cos Р-8 со 2 п Или ЛП с cos Р-8 cos4 Ф 8 sin4 Ф. Затем находим значение этой производной в первом положении равновесия, подставляя значение 0. О п д р 7×0. Согласно 8, начальное равновесие неустойчиво. Во 2-м положении равновесия arccos Л- 44 2-е положение равновесия является стабильным. Задача 18. 4.
Масса m массы p может перемещаться в вертикальной плоскости по гладкой окружности радиуса r. Точки притягиваются к 2 центрам a и b, которые симметричны центру окружности и находятся в горизонтальном диаметре. Факт, сила прямо пропорциональна расстоянию fa — ma, fb — — mb, где ce, 0-постоянный коэффициент. Расстояние ОА ОВ а. На какой угол точки М в равновесии Исследуйте устойчивость точки равновесия. Решение. 3 активные силы действуют на точку m.
Гравитация p направлена вертикально вниз, а 2 гравитационные силы направлены соответственно на ma и mv. Возможное движение точки m направлено по касательной к окружности и равно модулю Р 0С. Создайте базовое движение со всей своей мощью. Гладкая круговая реакция является нормальной для возможного смещения. Поэтому ее работа равна нулю. Задача гравитации — 6 41 СПКЯ pr 6 p. Для расчета работы притяжения lm lu ol, l lu oo lu-oa И так оно и есть. РД а МО ОА, ФС МО-ОА.
Потому что вектор МО перпендикулярен возможному смещению ФД БЗ — в АР БФ грех Ф, ФБ БЗ Р АР БФ грех Ф. Таким образом, основной работой всех сил при возможном перемещении является ба Р pso5ph Р-А avy1f БФ. 1 Так. Р СПКЯ П-а azshf 2 Если уравнять эту формулу до нуля, то мы найдем точку равновесия. — Иммуноглобулин — Следующий р -г — pv1pf р — а asozf Или рассмотрим равенство 3 Здесь вы можете вспомнить 4 случая. 1 для a p и угла y, — 0 2 Если a p и угол y, то p- 0. В этих случаях положение равновесия устойчиво, и точка м находится в 1-м или 2-м квадранте нижней половины окружности. 3 Если a p и л, 0 4 Если a p и — — l 2n, — 0.
В последних 2 случаях положение равновесия неустойчиво, и точка m находится в 3-м или 4-м квадранте верхней половины окружности. К заданию 18. 5. Задание 18. 5. Двойной маятник состоит из стержней длиной ОА 4 и ЛВ b, которые соединены шарнирами друг с другом и шарнирно закреплены на основании в точке о. Сила тяжести pj в точке a и сила ra в точке b. С помощью шарниров o и a спиральная пружина прикреплена к стержню, и когда маятник находится в вертикальном положении, он не деформируется. Определите жесткость спиральной пружины, не обращая внимания на трение соединения. Это стабилизирует положение вертикального равновесия. Решение. Система имеет 2 степени свободы.
В качестве обобщенных координат берутся углы px и phi, определяющие отклонение стержня маятника от вертикали. Направьте ось y вверх, а ось x вправо, чтобы представить потенциальную энергию системы как сумму потенциальной энергии гравитации и потенциальной энергии спирали. Он будет возникать. Когда ось x является нулевым уровнем потенциальной энергии силы тяжести маятника, маятник представлен выражением. Пх р1л р нет. Здесь координаты определяются через координаты, обобщенные по формуле ji 4cos ft, yt zx cosФ1 la cosф9. Так. .Пх ptzx cosф1 pt Z1 Cosф, Z9 Cosф9 Pl 4 cosфх PJT COSФ энергия положения спиральной пружины равна НС -г-С1ф уС ф1-Ф1У, 2 второй пружины, торсионный угол ф9-фх равны.
Потенциальная энергия системы Р РХ Р Р Р р на ZX cosф1 П. З. cosфа С1ф с фа-Ф1 1 1 Сильвестра теорема, в соответствии с 2 степенями свободы системы, которая должна быть стабильной, квадратичная форма матрицы основные минор 1 необходимо и достаточно.
Был положительным D, si 0, 2 Д, I u UI СсСя-CIA 0.3 МЦМНИР считайте, что это c si .cc 0, поэтому он идет от 3 до cm 0.Переходим к расчету обобщенного коэффициента жесткости по формуле д н б н, б н Вводя потенциальную энергию 1 в эти уравнения, первый — Пи р 4sin Пи ки Пи-Ки ПС-ЧЧ — В СЛН Р4 С8 Р, — Пи В дальнейшем КР 5.I — 1 4 COS P1 1 — A 1 4 1 e 4 22 P Z C0S Л — RA 5 Согласно условиям 2, 3 и их результатам cm 0, верхнее равновесное положение маятника равно- 0 7 в случае стабилизации.— Pi PJ 4 i s .— Р 4 Ч — — с 0.8 Из 7 F P 4 — 9 Если равенство 8 делится на c —P 4 — 1 А 4 м-о — 4-е.
Смотрите также:
Предмет теоретическая механика
