Задача C8. Два автомобиля движутся co скоростями 36 км/ч и 54 км/ч под углом 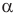 = 60° друг к другу. В некоторый момент времени один из них оказался в пункте М, а другой в тот же момент — в пункте N, расстояние между которыми S = 10 км.
= 60° друг к другу. В некоторый момент времени один из них оказался в пункте М, а другой в тот же момент — в пункте N, расстояние между которыми S = 10 км.
Через какой промежуток времени t расстояние между автомобилями станет минимальным?
Обозначим v — скорость автомобиля слева на рис. 49, 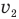 — скорость автомобиля справа,
— скорость автомобиля справа, 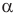 — угол между направлениями скоростей автомобилей, S — расстояние между ними в начальный момент наблюдения,
— угол между направлениями скоростей автомобилей, S — расстояние между ними в начальный момент наблюдения,
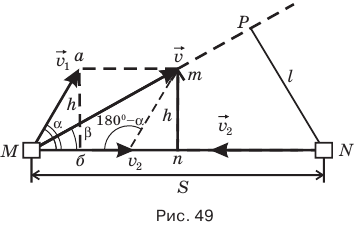
t — промежуток времени, через который расстояние между автомобилями станет минимальным, v — скорость автомобиля слева, если бы автомобиль справа был неподвижен, l — кратчайшее расстояние между обоими автомобилями, L — путь, пройденный левым автомобилем со скоростью V, Р — один из острых углов треугольника Мmn, h — длину перпендикуляра, опущенного из конца вектора 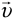 на отрезок MN.
на отрезок MN.

Решение:
Как же определить момент времени, когда расстояние между автомобилями станет наименьшим? Они же все время едут, причем каждый со своей скоростью — попробуй поймать этот самый момент.
Сразу дадим совет: при решении подобных задач, когда два тела одновременно движутся относительно друг друга, примите одно из них, например, автомобиль справа, за неподвижное, тогда можно считать, что автомобиль слева, продолжая двигаться со своей скоростью 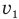 станет приближаться к правому автомобилю в пункте N с его скоростью
станет приближаться к правому автомобилю в пункте N с его скоростью 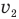 , но вектор которой направлен противоположно, т.е. навстречу правому автомобилю. Теперь заменим эти две скорости левого автомобиля одной скоростью v, сложив их векторы. При этом модуль вектора
, но вектор которой направлен противоположно, т.е. навстречу правому автомобилю. Теперь заменим эти две скорости левого автомобиля одной скоростью v, сложив их векторы. При этом модуль вектора 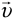 будет равен длине диагонали параллелограмма, построенного на векторах этих скоростей, как на сторонах. Прямая МР, вдоль которой направлен вектор скорости
будет равен длине диагонали параллелограмма, построенного на векторах этих скоростей, как на сторонах. Прямая МР, вдоль которой направлен вектор скорости 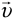 , и будет той траекторией, по которой будет двигаться левый автомобиль, если принять правый за неподвижный.
, и будет той траекторией, по которой будет двигаться левый автомобиль, если принять правый за неподвижный.
Если теперь из точки N, где находится правый неподвижный автомобиль, опустить перпендикуляр NP на эту траекторию, то длина этого перпендикуляра l и будет тем самым кратчайшим расстоянием между обоими автомобилями. Искомый промежуток времени t можно найти, если разделить путь L, пройденный левым автомобилем со скоростью v и равный длине отрезка МР, на эту скорость:
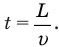
Скорость v найти несложно. В тупоугольном треугольнике скоростей вектор этой скорости лежит против тупого угла, равного 180° — 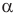 , а две другие стороны этого треугольника равны по модулю скоростям
, а две другие стороны этого треугольника равны по модулю скоростям 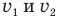 , поэтому согласно теореме косинусов
, поэтому согласно теореме косинусов
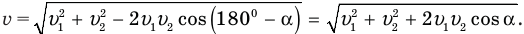
Труднее определить длину отрезка L = МР. Этот отрезок является катетом в прямоугольном треугольнике MPN, где гипотенузой служит известное нам расстояние S=MN, а другим катетом — неизвестный отрезок l. Этот треугольник прямоугольный, но и от этого мало радости, ведь отрезок l взять неоткуда. Вот если бы в этом треугольнике нам был известен очень острый угол PMN, мы тогда могли найти катет L через прилежащий к этому катету угол PMN и гипотенузу S.
Но как определить этот острый угол? Обозначим его как-нибудь, например, 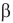 . Может, его можно определить через векторы скоростей, между которыми он заключен? Но как? Вот если б этот угол входил в еще какой-нибудь треугольник. А что если его построить? Давайте опустим из конца вектора и на отрезок MN перпендикуляр mn и обозначим его высоту h. Теперь у нас есть прямоугольный треугольник Мmn, в котором гипотенузой служит скорость о, а угол
. Может, его можно определить через векторы скоростей, между которыми он заключен? Но как? Вот если б этот угол входил в еще какой-нибудь треугольник. А что если его построить? Давайте опустим из конца вектора и на отрезок MN перпендикуляр mn и обозначим его высоту h. Теперь у нас есть прямоугольный треугольник Мmn, в котором гипотенузой служит скорость о, а угол 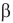 является одним из острых углов этого треугольника. Но опять же нам не известен отрезок h. Похоже, мы в тупике.
является одним из острых углов этого треугольника. Но опять же нам не известен отрезок h. Похоже, мы в тупике.
Вот если бы как-нибудь найти этот h. Может, опустить из конца вектора скорости 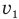 еще один перпендикуляр ab такой же высоты? А что? — это идея! Теперь мы можем выразить отрезок h из прямоугольного треугольника МаЬ через скорость
еще один перпендикуляр ab такой же высоты? А что? — это идея! Теперь мы можем выразить отрезок h из прямоугольного треугольника МаЬ через скорость 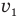 и противолежащий этому перпендикуляру известный нам угол
и противолежащий этому перпендикуляру известный нам угол 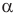 :
:
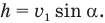
Зная h, находим из прямоугольного треугольника Мmn 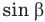 :
:
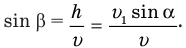
Теперь уже просто. Из прямоугольного треугольника MPN выражаем катет L через известную нам гипотенузу S и найденный угол 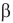 :
:
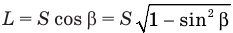
или с учетом (4)
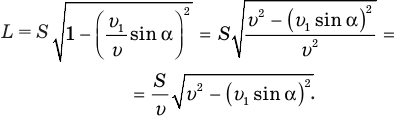
Нам осталось подставить правые части равенств (2) и (5) в формулу (1), и непростая задача, потребовавшая от нас столько выдумки и сообразительности, будет решена. Подставляем:
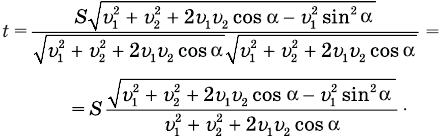
В общем-то задача решена, но хорошо бы полученную формулу упростить. Сделать это несложно. Достаточно сгруппировать под корнем первый и последний члены, вынести 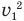 за скобки и вспомнить, что
за скобки и вспомнить, что
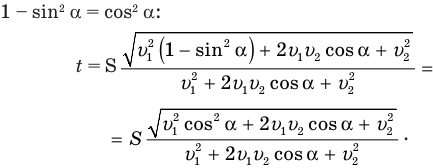
Теперь мы видим, что под корнем стоит квадрат суммы величин 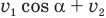 :
:
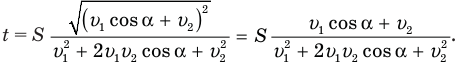
Выразим все величины в единицах СИ: 36 км/ч = 10 м/с, 54 км/ч = 15 м/с, 10 км = 1- 10* м.
Подставим числа и произведем вычисления:
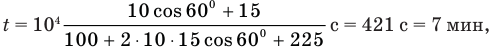
Ответ: t = 7 мин.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
