Оглавление:
Теорема о сложении скоростей
Теорема. Абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей
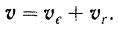
Доказательство. Пусть точка 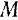 движется относительно некоторой подвижной системы
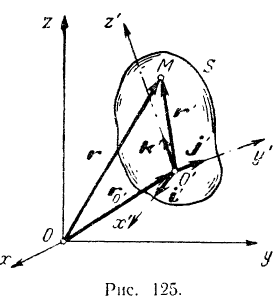
движется относительно некоторой подвижной системы 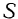 отсчета и имеете с этой системой перемещается относительно неподвижной системы отсчета (рис. 125).
отсчета и имеете с этой системой перемещается относительно неподвижной системы отсчета (рис. 125).
За начало новой (недвижной) системы координатных осей 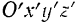 , неизменно связанных с подвижной системой
, неизменно связанных с подвижной системой 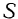 , примем какую-нибудь произвольную точку
, примем какую-нибудь произвольную точку  этой системы. Положение точки
этой системы. Положение точки 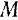 относительно подвижной системы отсчета определяется радиусом-вектором
относительно подвижной системы отсчета определяется радиусом-вектором 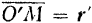 .
.
Если отложить на осях подвижной системы координат единичные векторы 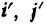 и
и 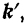 то по формуле (55) можно записать, что
то по формуле (55) можно записать, что
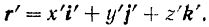
Относительная скорость 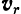 точки
точки 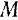 равна производной по времени от радиуса-вектора
равна производной по времени от радиуса-вектора 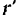 этой точки. Для того чтобы ее определить, нужно мысленно остановить переносное движение (т. е. подвижную систему отсчета) и считать, следовательно, орты
этой точки. Для того чтобы ее определить, нужно мысленно остановить переносное движение (т. е. подвижную систему отсчета) и считать, следовательно, орты 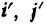 и
и 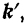 постоянными векторами. В этом случае, дифференцируя равенство (I), получим:
постоянными векторами. В этом случае, дифференцируя равенство (I), получим:
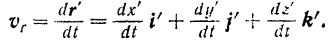
Положение начала  подвижной системы
подвижной системы 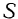 относительно неподвижной системы определяется радиусом-вектором
относительно неподвижной системы определяется радиусом-вектором
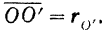
Положение точки 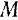 относительно неподвижной системы отсчета определяется радиусом-вектором
относительно неподвижной системы отсчета определяется радиусом-вектором
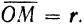
Как видно из векторного треугольника 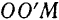 (рис, 125):
(рис, 125):
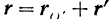
или, если подставить сюда выражение (I) для 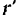 ,
,
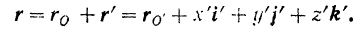
Для того чтобы определить переносную скорость 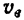 точки
точки 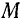 , надо мысленно остановить относительное движение точки и определить ее скорость как точки, неизменно связанной с подвижной системой
, надо мысленно остановить относительное движение точки и определить ее скорость как точки, неизменно связанной с подвижной системой 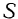 . Следовательно, переносную скорость точки можно найти, дифференцируя по времени равенство (III), полагая при этом координаты
. Следовательно, переносную скорость точки можно найти, дифференцируя по времени равенство (III), полагая при этом координаты 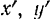 и
и 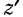 точки
точки 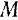 относительно подвижной системы отсчета постоянными величинами.
относительно подвижной системы отсчета постоянными величинами.
В этом случае, дифференцируя равенство (III), получим:
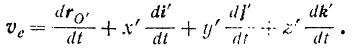
Определим теперь абсолютную скорость с точки 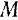 . При произвольном движении подвижной системы
. При произвольном движении подвижной системы 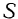 и неизменно связанных с ней координатных осей орты
и неизменно связанных с ней координатных осей орты 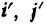 и
и 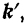 изменяют свое направление и являются переменными векторами. При движении точки
изменяют свое направление и являются переменными векторами. При движении точки 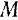 относительно подвижной системы
относительно подвижной системы 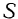 переменными будут и ее координаты
переменными будут и ее координаты 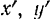 и
и 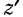 . Таким образом, при определении абсолютной скорости точки
. Таким образом, при определении абсолютной скорости точки 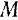 все члены, входящие в равенство (III), надо считать переменными.
все члены, входящие в равенство (III), надо считать переменными.
В этом случае, дифференцируя равенство (III), получим:
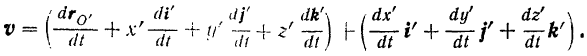
Нетрудно видеть, что первое из двух выражений, стоящих в правой част последнего равенства и заключенных нами (для удобства) в скобки, представляет собой правую часть равенства (IV), т. с. переносную v,, скорость точки. Второе из этих выражений представляет собой правую часть равенства (II), т. с. относительную скорость 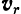 точки.
точки.
Следовательно,
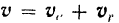
и теорема доказана.
Так как абсолютная скорость 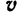 точки находится по общему правилу сложения двух векторов, т. е. изображается диагональю параллелограмма, построенного на
точки находится по общему правилу сложения двух векторов, т. е. изображается диагональю параллелограмма, построенного на
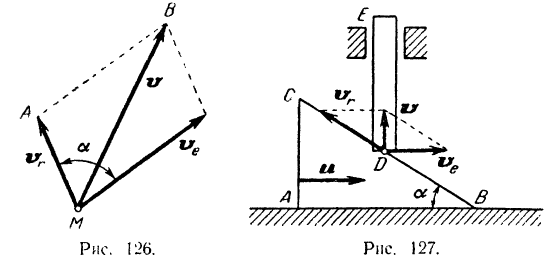
векторах ее переносной 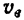 и относительной
и относительной 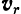 скоростей (рис. 126), то доказанную теорему называют часто теоремой параллелограмма скоростей.
скоростей (рис. 126), то доказанную теорему называют часто теоремой параллелограмма скоростей.
Пример задачи:
Кулачок, имеющий форму клипа 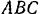 с углом
с углом 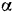 (рис. 127), движется поступательно по горизонтальной плоскости со скоростью
(рис. 127), движется поступательно по горизонтальной плоскости со скоростью 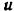 . Определить скорость стержня (толкателя)
. Определить скорость стержня (толкателя) 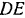 . опирающегося на кулачок и свободно скользящего в неподвижных направляющих.
. опирающегося на кулачок и свободно скользящего в неподвижных направляющих.
Решение:
При движении клина вправо стержень 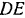 получает поступательное движение по вертикали вверх. Так как при поступательном движении стержня все его точки имеют одинаковые скорости, то найдем скорость одной точки
получает поступательное движение по вертикали вверх. Так как при поступательном движении стержня все его точки имеют одинаковые скорости, то найдем скорость одной точки 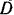 . Если мы примем за систему отсчета клин, то по отношению к нему точка
. Если мы примем за систему отсчета клин, то по отношению к нему точка 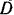 перемещается вдоль прямой
перемещается вдоль прямой 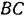 . Так как сам клин также движется по отношению к неподвижной системе отсчета, то движение точки
. Так как сам клин также движется по отношению к неподвижной системе отсчета, то движение точки 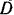 по отношению к клину будет относительным движением, движение же этой точки имеете с клином — переносным движением.
по отношению к клину будет относительным движением, движение же этой точки имеете с клином — переносным движением.
Направление относительной 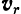 и абсолютной
и абсолютной 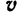 скоростей точки
скоростей точки 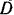 нам извести. Наличие неподвижных направляющих позволяет стержню (и его точке
нам извести. Наличие неподвижных направляющих позволяет стержню (и его точке 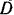 ) иметь только одно движение по отношению к неподвижной системе отсчета — вертикальное.
) иметь только одно движение по отношению к неподвижной системе отсчета — вертикальное.
Переносная скорость точки 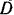 известна и по величине, и по направлению:
известна и по величине, и по направлению:  . Строим параллелограмм скоростей точки
. Строим параллелограмм скоростей точки 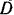 . Из конца вектора
. Из конца вектора 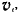 переносной скорости точки
переносной скорости точки 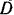 проводим прямую, параллельную относительной скорости (прямой
проводим прямую, параллельную относительной скорости (прямой 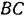 ), до пересечения ее с прямой
), до пересечения ее с прямой 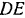 , по которой направлена абсолютная скорость.
, по которой направлена абсолютная скорость.
Из прямоугольного треугольника скоростей находим:
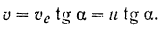
Пример задачи:
Кривошипы 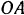 и
и 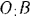 паровозных осей
паровозных осей 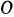 и
и 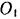 (рис. 128) длиной
(рис. 128) длиной
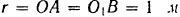
вращаются с постоянной
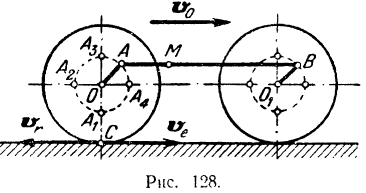
угловой скоростью
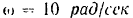
и соединены между собой спарником 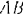 . Радиусы колее
. Радиусы колее 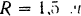 . Колеса катятся по рельсам без скольжения. Определить абсолютную скорость любой точки
. Колеса катятся по рельсам без скольжения. Определить абсолютную скорость любой точки 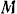 спарника
спарника 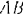 для четырех, указанных на рис. 128, положений кривошипа.
для четырех, указанных на рис. 128, положений кривошипа.
Решение:
Так как спарник 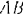 совершает поступательное движение, то скорости всех его точек одинаковы. Скорость точки
совершает поступательное движение, то скорости всех его точек одинаковы. Скорость точки 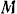 равна скорости точки
равна скорости точки 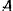 , в которой конец спарника шарнирно соединен с кривошипом
, в которой конец спарника шарнирно соединен с кривошипом 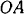 . Точку
. Точку 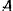 можно считать участвующей в двух движениях, в относительном — вращательном движении вокруг оси
можно считать участвующей в двух движениях, в относительном — вращательном движении вокруг оси 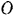 и в переносном — вместе с паровозом в его поступательном движении со скоростью, равной скорости
и в переносном — вместе с паровозом в его поступательном движении со скоростью, равной скорости 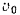 оси
оси 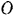 колеса. Найдем скорость
колеса. Найдем скорость 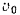 оси
оси 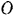 или, что то же, скорость паровоза. Рассмотрим движение точки колеса, в которой оно касается рельса. Эта точка также участвует в двух движениях: в переносном, со скоростью
или, что то же, скорость паровоза. Рассмотрим движение точки колеса, в которой оно касается рельса. Эта точка также участвует в двух движениях: в переносном, со скоростью 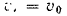 и в относительном — вращательном вокруг оси
и в относительном — вращательном вокруг оси 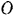 . Относительная скорость
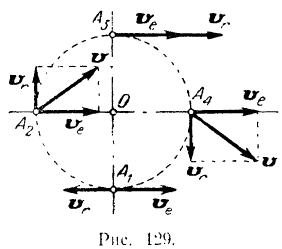
. Относительная скорость 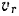 точки должна быть, очевидно, направлена (так, как показано на рис. 129) по касательной окружности колеса в сторону его вращения и равна по модулю
точки должна быть, очевидно, направлена (так, как показано на рис. 129) по касательной окружности колеса в сторону его вращения и равна по модулю 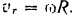
Но колесо катится без скольжения, поэтому абсолютная скорость точки касания колеса с рельсом должна равняться нулю. Отсюда, так как переносное и относительное движения точки 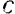 направлены по одной прямой в противоположные стороны, имеем:
направлены по одной прямой в противоположные стороны, имеем:
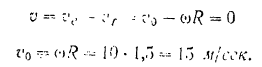
Модуль относительной скорости точки 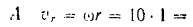
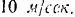 Направление же этой скорости меняется в зависимости от положения точки
Направление же этой скорости меняется в зависимости от положения точки 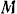 . Переносная скорость этой точки
. Переносная скорость этой точки 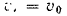 . Строим теперь (рис. 129) параллелограммы скоростей для различных положений кривошипа и из них определяем модуль и направление абсолютной скорости точки:
. Строим теперь (рис. 129) параллелограммы скоростей для различных положений кривошипа и из них определяем модуль и направление абсолютной скорости точки:
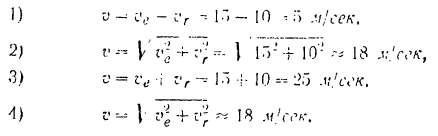
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
