Оглавление:




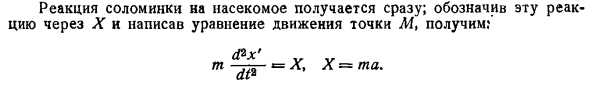

Доказательство теоремы количества движения
- Предположим, что уравнение 1 записано для всех точек системы. Давайте обобщим все эти уравнения. Что взять. Где знак 22 указывает, что сумма распространяется на все силы, действующие на каждую точку системы. Однако по закону равенства действия и противодействия внутренние силы попарно равны и направлены в противоположные стороны. Таким образом, общее число 22 равно нулю, а предыдущее уравнение равно ДТ Или эти уравнения также могут быть записаны следующим образом: Или Выразите теорему импульса системы и теорему предсказания импульса. Теорема производная по времени от суммы числа точек движения системы равна сумме внешних сил.
Теорема производная по времени от суммы проекций числа перемещений точек системы по неподвижной оси равна сумме проекций внешних сил на ту же ось. Например, если= m0 S m = const Формула 2 допускает другую интерпретацию. В эд представлена полная масса 2М, м после С находится координата центра тяжести системы и выглядит так: Эд = 2 МХ = 2 млн = 2 н р Уравнение 2 описывается в виде: = = = 22 3 Эта форма представляет следующие свойства: Теорема центр тяжести системы параллелен, масса равна общей массе системы и движется как точка материи, к которой приложена сила, равная внешней силе системы.
Установить формулы такого же, как в примере 14, характера для движения точки на поверхности вращения под действием силы, постоянно находящейся в плоскости меридиана движущейся точки. Людмила Фирмаль
Эта теорема, уже использованная, представляет интерес, помимо прочего, в том смысле, что она придает истинный смысл теории движения важных точек. Она получила название теоремы о движении центра тяжести. Эта теорема была указана Ньютоном в некоторых случаях. Образцы. 1.Отсутствие внешних сил. Самое простое предположение, которое мы можем сделать, заключается в том, что внешняя сила не действует на систему. Тогда центр тяжести системы совершит прямое и равномерное движение.
Например, если предположить, что движение звезды в Солнечной системе равно нулю, то центр тяжести этой системы, находящийся очень близко к Солнцу, будет иметь линейное и равномерное движение. 2.Тяжелая система в пустоте. Теперь рассмотрим систему тяжелых точек, брошенных в пустоту. Каким бы ни был вариант или внутреннее соединение системы, ее центр тяжести рисует параболу с вертикалью axis. In дело в том, что различные внешние силы вертикальны. Если они перемещаются к центру тяжести, мы получаем центр в результате Гравитация движется как тяжелая масса Эд.
Например, если бомба брошена в пустоту и в какой то момент взрывается, центр тяжести обломков будет продолжать рисовать ту же параболу, так как сила, возникающая при взрыве, является внутренней. Точно так же, если существо движется в пустоте только под действием своего веса, его центр тяжести представляет собой параболу, и мышечное усилие, которое оно производит, не изменяет траекторию его центра тяжести. Эти усилия внутренние силы. 3.Гравитация пропорциональна distance. It также принимается система материальных точек, которые притягиваются к неподвижному центру O, пропорционально массе и расстоянию R. внешняя сила, центральная сила притяжения fmr. Перенесите эти силы на центр тяжести G.
Тогда, как мы видели со статикой, результат ориентируется вдоль ГО и имеет значение ftylGO. As в результате центроид перемещается как материальная точка, которая притягивается к точке O пропорционально расстоянию. Представляет собой эллипс, центрированный в точке O. Обратите внимание, что в предыдущих 2 примерах мы смогли определить движение центра тяжести, ничего не зная о связи или внутренней силе. Это стало возможным благодаря тому, что в указанном случае правая часть уравнения 3 зависит, 1, С и вы можете интегрировать эти уравнения, не зная никакого другого уравнения motion. In генерал, это не работает.
- Правая часть уравнения 3 зависит от координат всех точек в системе, и эти уравнения дают лишь некоторое представление о движении. Такие случаи возникают, например, в вопросе о движении 2 точек, которые, согласно закону Ньютона, притягиваются друг к другу и к неподвижной точке. center. In в этом случае Объединенные силы внешних сил, передаваемые центру тяжести, зависят не только от координат центра тяжести, но и от координат самой точки. 4.Ходьба Делоне, механика Д Е 1 А и Ла, xM6canique. как уже говорилось в Примере, теорема о движении центра тяжести распространяется и на живые организмы.
Мышечное усилие, возникающее в результате сокращения мышц, равно диаметрально противоположно внутренним силам в паре. Поэтому она не влияет на движение центра тяжести. Таким образом, существо может изменить движение своего центра тяжести только с внешней помощью. Например, представьте себе наблюдателя, стоящего на идеально отполированной горизонтальной поверхности. Все внешние силы, действующие на тело наблюдателя вес самолета и вертикальное противодействие вертикальны. Если наблюдатель вначале не движется, а затем хочет двигаться, то его центр тяжести, поначалу, не движется, а под действием вертикальной силы движется подобно материальной точке.
Движение точки на сфере под действием силы, постоянно лежащей в плоскости меридиана, проходящего через движущуюся точку. Людмила Фирмаль
Эта точка представляет собой фиксированную вертикальную линию. Поэтому мышечное усилие не изменяет горизонтальной проекции центра тела. gravity. In в этом случае ходьба не является allowed. It возможно только трение. На негладком грунте, когда человек, который сначала не двигается, поднимает одну ногу вперед, горизонтальная проекция центра тяжести не меняется, а другая стремится отодвинуться назад. Но 2 я нога не может вернуться, кроме скольжения по земле. Это приводит к тому, что трение с землей отклоняется от вертикали и вызывает реакцию, направленную вперед. Это противодействие движется параллельно себе с центром тяжести и определяет его поступательное движение.
Отдача огнестрельного оружия. Рассмотрим массу M горизонтальной пушки. пусть m масса снаряда, а p масса снаряда. Масса частиц пороха скорость центра тяжести равна нулю до того, как порох будет сожжен. Так как действие массы и пассивное сопротивление в течение очень короткого периода горения можно считать равным нулю, то сразу после сгорания порошка только генерирующая сила будет внутренней, поэтому она должна оставаться same. So, если вы представляете абсолютное значение начальной скорости пушки, снаряда и частицы p в V, v и w, то: Л В МВ да. Знаки скорости снаряда и частиц пороха явно противоположны знакам скорости орудия.
Знак 2 обозначает суммарный распространенный на все частицы заряд. Так как скорость w неизвестна, а масса = заряд не достигает 4 мин 1 массы m, то можно принять w, которое приблизительно равно алгебраическому mean. In сюда Уравнение чая V 2Af 4 m = V 2t 4 m Коэффициент определения скорости V и 6.Упражнение. Прямые соломинки AB длиной 21 и массой t укладываются на идеально отполированную горизонтальную поверхность рис.183. h— 4 1 0 М Г Ц Ч Х д Рисунок 183. Та же масса насекомого М, которая считается точкой, изначально перестала двигаться в конце A.
В момент времени t = 0 мы начинаем двигаться от A к B и совершаем равномерно ускоренные движения вдоль AB AM = at2. Что такое движение системы Поскольку внешняя сила является только весом горизонтальной плоскости и нормальной реактивной силой, горизонтальная проекция центра тяжести остается motionless. In кроме того, ясно, что по соображениям симметрии соломинка AB движется только в исходном направлении. Пусть это направление ось Ox, координаты C и M средних точек отрезков x и x AB, а x значения этих координат в момент времени = 0. + = + С х = х 4 АТ2, хо = хо я Тогда возьми его. АТ2 Два Реакция соломы на червей X = Xq происходит мгновенно.
Смотрите также:
Решение задач по теоретической механике
