Оглавление:
Эквивалентные бесконечно малые функции
Сравнение бесконечно малых функций
Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно боль той функцией, бесконечно малой или вообще не стремиться ни к ка кому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть 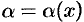 и
и 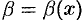 есть б.м.ф. при
есть б.м.ф. при 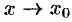 , т. е.
, т. е. 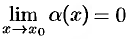 и
и 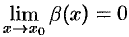 .
.
1. Если 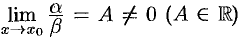 , то
, то 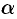 и
и 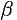 называются бесконечно малыми одного порядка.
называются бесконечно малыми одного порядка.
2. Если 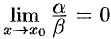 , то
, то 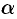 называется бесконечно малой более высокого порядка, чем
называется бесконечно малой более высокого порядка, чем 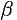 .
.
3. Если 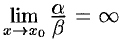 , то
, то 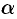 называется бесконечно малой более низкого порядка, чем
называется бесконечно малой более низкого порядка, чем 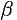 .
.
4. Если 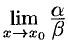 не существует, то
не существует, то 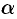 и
и 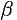 называются несравнимыми бесконечно малыми.
называются несравнимыми бесконечно малыми.
Отметим, что таковы же правила сравнения б.м.ф. при 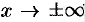 ,
, 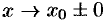 .
.
Пример №18.1.
Сравнить порядок функций 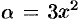 и
и 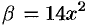 при
при 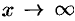 .
.
Решение:
При 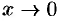 это б.м.ф. одного порядка, так как
это б.м.ф. одного порядка, так как
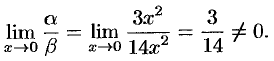
Говорят, что б.м.ф. 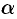 и
и 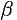 одного порядка стремятся к нулю с примерно одинаковой скоростью.
одного порядка стремятся к нулю с примерно одинаковой скоростью.
Дополнительные примеры:
Эквивалентные бесконечно малые функции и основные теоремы о них
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.
Если 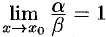 , то
, то 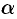 и
и 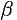 называются эквивалентными бесконечно малыми (при
называются эквивалентными бесконечно малыми (при 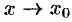 ); это обозначается так:
); это обозначается так: 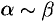 .
.
Например, 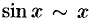 при
при 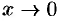 , т. к.
, т. к. 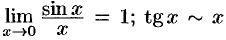 при
при 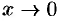 , т. к.
, т. к. 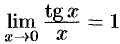 .
.
Теорема 18.1. Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
Пусть 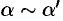 и
и 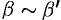 при
при 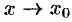 . Тогда
. Тогда
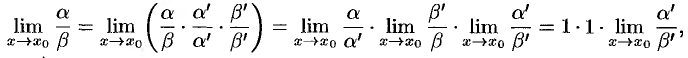
т. е. 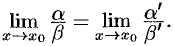
Очевидно также, что 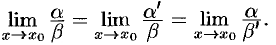
Теорема 18.2. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.
Пусть 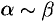 при
при 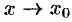 . Тогда
. Тогда
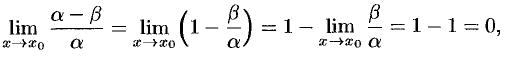
аналогично 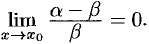
Справедливо и обратное утверждение-. если разность б.м.ф. 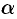 и
и 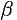 есть бесконечно малая высшего порядка, чем
есть бесконечно малая высшего порядка, чем 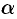 или
или 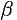 , то
, то 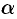 и
и 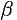 — эквивалентные бесконечно малые.
— эквивалентные бесконечно малые.
Действительно, так как 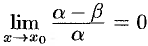 , то
, то 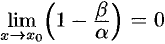 , т. е.
, т. е. 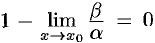 . Отсюда
. Отсюда 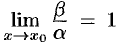 , т. е.
, т. е. 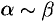 . Аналогично, если
. Аналогично, если 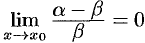 , то
, то 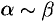 .
.
Теорема 18.3. Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Докажем теорему для двух функций. Пусть 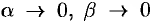 при
при 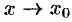 , причем
, причем 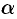 — б.м.ф. высшего порядка, чем
— б.м.ф. высшего порядка, чем 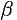 , т. е.
, т. е. 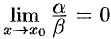 . Тогда
. Тогда
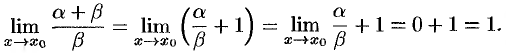
Следовательно, 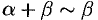 при
при 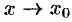 .
.
Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы.
Замена суммы б.м.ф. ее главной частью называется отбрасыванием бесконечно малых высшего порядка.
Пример №18.5.
Найти предел 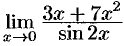 .
.
Решение:
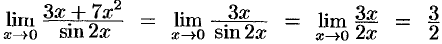 , поскольку
, поскольку 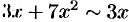 и
и 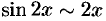 при
при 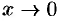 .
.
Применение эквивалентных бесконечно малых функций
Вычисление пределов
Для раскрытия неопределённостей вида 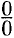 часто бывают полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно,
часто бывают полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно, 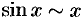 при
при 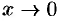 ,
, 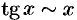 при
при 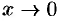 . Приведем еще примеры эквивалентных б.м.ф.
. Приведем еще примеры эквивалентных б.м.ф.
Пример №18.6.
Покажем, что 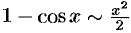 при
при 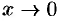 .
.
Решение:
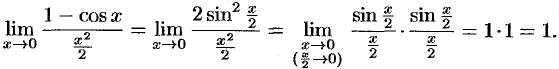
Дополнительные примеры:
Приближенные вычисления
Если 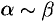 , то, отбрасывая в равенстве
, то, отбрасывая в равенстве 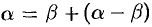 бесконечно малую более высокого порядка, т. е.
бесконечно малую более высокого порядка, т. е.  , получим приближенное равенство
, получим приближенное равенство 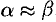 .
.
Оно позволяет выражать одни бесконечно малые через другие. Приведенные выше важнейшие эквивалентности служат источником ряда приближенных формул.
Приведенные формулы справедливы при малых  , и они тем точнее, чем меньше
, и они тем точнее, чем меньше  .
.
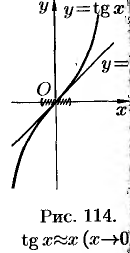
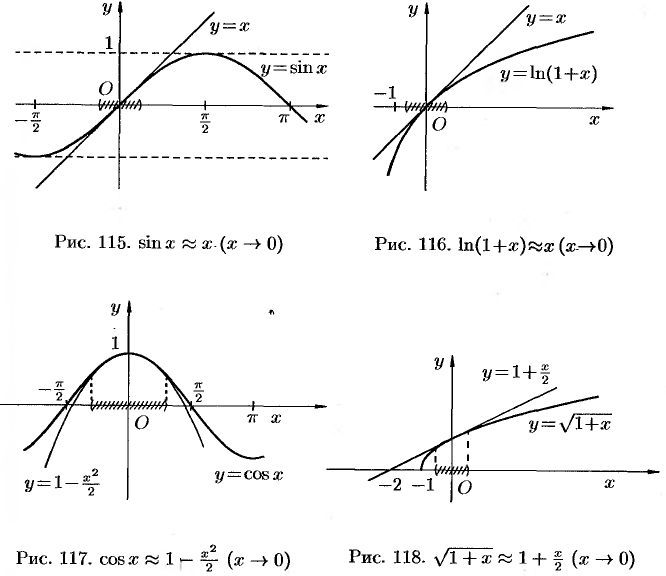
Например, графики функций 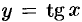 и
и 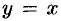 в окрестности точки 0 практически не различимы (см. рис. 114), а кривая
в окрестности точки 0 практически не различимы (см. рис. 114), а кривая 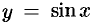 в окрестности точки 0 сливается с прямой
в окрестности точки 0 сливается с прямой 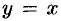 (рис. 115). На рисунках 116-118 проиллюстрированы некоторые из важнейших эквивалентностей, о которых говорилось выше.
(рис. 115). На рисунках 116-118 проиллюстрированы некоторые из важнейших эквивалентностей, о которых говорилось выше.
Пример №18.12.
Найти приближенное значение для 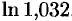 .
.
Решение:
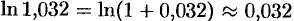 . Для сравнения результата но таблице логарифмов находим, что
. Для сравнения результата но таблице логарифмов находим, что 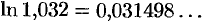
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
