Оглавление:
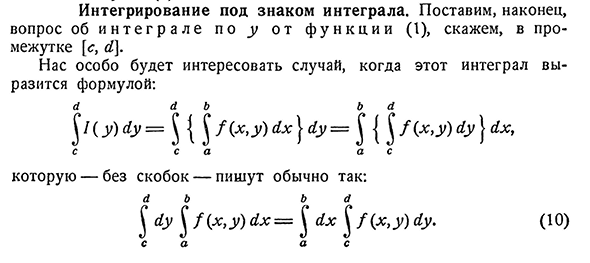



Интегрирование под знаком интеграла
- Интеграл под знаком интеграла. Давайте, наконец, поставим мой вопрос I (1), например, в интервале[s, y], от f U n R E l e до u C I. Особый интерес представляет, если этот Интеграл выражается следующей
формулой: a b b a/(x, y) (1x^(1y= ы ы ы ы И Это-без скобок-обычно пишется следующим образом: 144CHAP. Интеграл, зависящий от параметров[298 Когда она существует, говорят, что функция (1)
может быть интегрирована параметром y»z n A K o m и n T e g R a l a L a» Людмила Фирмаль
(взятой переменной x). Простейшее условие, достаточное для равенства двух повторяющихся интегралов(10), задается теоремой 4. Если функция / (x,y)прямоугольника[a,B;C,b]непрерывна, то выполняется выражение (10). Мы докажем более общее равенство 7] Б В7] БУ/(х, г) х б=б х/(х, 3/)БУ,(уа) С А А С а с Где С7] б. В его левой и
правой частях есть две функции от параметра t]. Внешний Интеграл слева имеет подынтегральное выражение (1), которое превосходит y благодаря теореме 2. Таким образом, его производная к верхней границе переменной равна подынтегральному числу, вычисленному по Y -^, то есть целому числу b/01)=/(x, h) LX. Но Правая часть (Ua)
- имеет Интеграл\I о (Х, Т]), где ЧД, с? (X, т])=^/(х,у)Бу; С Функция CP (x, t]) удовлетворяет условию теоремы 3. Действительно, CP (x, t]) является более непрерывным, чем x по теореме 2*). Далее его производные * ) Здесь роль параметра выполняет X. • » != = * >/(*Т)) Непрерывный как функция двух переменных. Таким образом, правило Лейбница
применяется к приведенному выше интегралу: b b y<0(x, — C) C1X==<?(х, — г^ых-Т])<1=1(•»])。 ля. Таким образом, левая и правая части равенства (10А) в зависимости от t]имеют равные производные, а потому могут отличаться только константами. Таким образом, они идентичны во всех значениях t и доказана их эквивалентность
(10A). Тогда при 71=6, в частности, также получается равенство(10).299]§1. Людмила Фирмаль
Элементарная теория 145 Это равенство было впервые упомянуто в 1769 году Эйлером (напечатано в следующем году). На это указывает только пример», поскольку основа этого вполне ясна из природы дифференциации и интеграции.»
Смотрите также:
Решение задач по математическому анализу
| Предельный переход под знаком интеграла | Случай, когда и пределы интеграла зависят от параметра |
| Дифференцирование под знаком интеграла | Определение равномерной сходимости интегралов |
