Оглавление:
Дифференциальное исчисление функции одной действительной переменной
Задание: Решение задач на нахождение производных и дифференциалов с использованием правил и формул дифференцирования.
Цель: формирование умения находить производные и дифференциалы функций, используя правила и формулы дифференцирования.
Задание для самостоятельной внеаудиторной работы:
12.1. Выучите определение производной функции в точке, с помощью таблицы «Формулы дифференцирования» проанализируйте, как находятся производные основных элементарных функций. Запомните правила дифференцирования функций и выясните, как они применяются. Изучите технику нахождения производной функции.
12.2. Найдите производную функции:
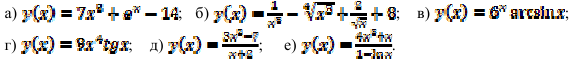
Вам известно, что к созданию дифференциального исчисления одновременно и независимо друг от друга в семнадцатом веке пришли гениальные ученые Исаак Ньютон и Готфрид Вильгельм Лейбниц. Они использовали абсолютно разные подходы. Концепция Лейбница базировалась на введенном им понятии дифференциала. Однако в научных кругах достаточно долго не утихала бурная дискуссия о приоритете изобретения дифференциального исчисления. Вероятно, именно ее имел в виду замечательный русский поэт, когда писал такие строки:

О Лейбниц, о мудрец, создатель вещих книг!
Ты выше мира был, как древние пророки.
Твой век, дивясь тебе, пророчеств не достиг
И с лестью смешивал безумные упреки.
Выполнив задание 12.2 и заменив получившиеся ответы буквами из таблицы, Вы узнаете фамилию автора стихотворения — поэта серебряного века.
Фамилия автора стихотворения:

Карта ответов:

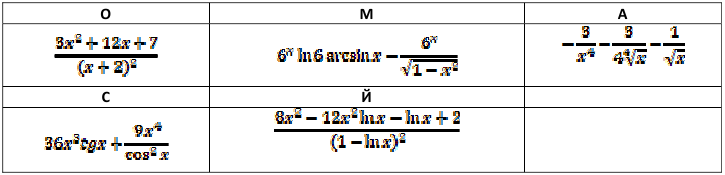
12.3. Выясните, как находится производная функции в точке.
12.4. Найдите производную функции в указанной точке:
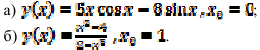
12.5. Выучите определение дифференциала функции и запомните формулу, которая используется для его нахождения.
12.6. Найдите дифференциал функции:
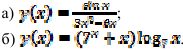
12.7. Выясните, при каких значениях  производная функции
производная функции 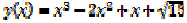 отрицательна.
отрицательна.
12.8. Найдите область определения функции, полученной в результате дифференцирования данной функции: 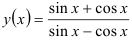 .
.
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Производной функции 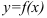 в точке
в точке  называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
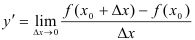 или
или 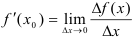 .
.
Производная функции 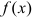 есть некоторая функция
есть некоторая функция 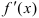 , производная из данной функции. Значение производной функции
, производная из данной функции. Значение производной функции 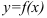 в точке
в точке 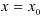 обозначается одним из символов:
обозначается одним из символов: 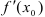 или
или 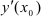 .
.
Функция 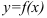 , имеющая производную в каждой точке интервала
, имеющая производную в каждой точке интервала 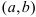 , называется дифференцируемой на этом интервале; операция нахождения производной функции называется дифференцированием.
, называется дифференцируемой на этом интервале; операция нахождения производной функции называется дифференцированием.
Для нахождения производных основных элементарных функций удобно использовать следующую таблицу: «Формулы дифференцирования».
Формулы дифференцирования:


В ряде случаев, если функция представляет собой сумму, разность, произведение или частное двух функций, для нахождения ее производной используются правила дифференцирования.
Пусть 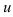 и
и 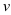 — дифференцируемые функции,
— дифференцируемые функции, 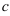 — константа. Тогда справедливы правила нахождения производной суммы, произведения и частного двух функций:
— константа. Тогда справедливы правила нахождения производной суммы, произведения и частного двух функций:
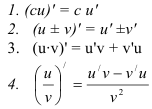
Таким образом, для нахождения производной функции удобно использовать следующую технику. Определите, что представляет собой функция. Если она является основной элементарной — для нахождения производной сразу используйте таблицу «Формулы дифференцирования». В тех случаях, когда перед Вами сумма, разность, произведение или частное функций — сначала используйте соответствующее правило дифференцирования, затем (для дифференцирования основной элементарной функции) таблицу «Формулы дифференцирования».
Рассмотрим примеры решения типовых задач.
Пример 1.
Найдите производную функции 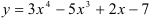 .
.
Решение:
Функция представляет собой сумму и разность функций. Тогда для нахождения её производной воспользуемся правилом 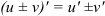 :
:
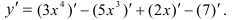
Константу можно вынести за знак производной по правилу: 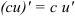 . Тогда
. Тогда
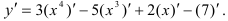
Далее воспользуемся формулами нахождения производных:
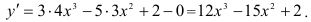
Ответ: 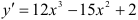 .
.
Пример 2.
Найдите производную функции 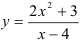 .
.
Решение:
Функция представляет собой частное функций. Тогда для нахождения её производной воспользуемся правилом 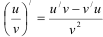 :
:
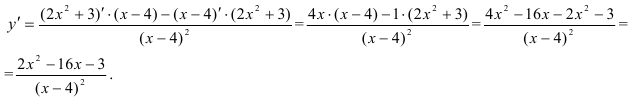
Ответ: 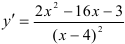 .
.
Если производная функции в общем случае представляет собой некоторую функцию, то производная функции в точке является числом. Для нахождения производной функции в точке надо продифференцировать данную функцию, а затем в полученное выражение вместо аргумента подставить указанную точку.
Пример 3.
Найдите производную функции 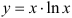 в точке
в точке 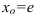 .
.
Решение:
Сначала найдем производную функции 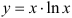 как производную произведения. Воспользуемся правилом
как производную произведения. Воспользуемся правилом 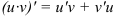 :
:
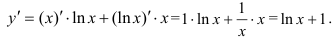
Для нахождения производной функции в точке в производную 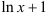 вместо аргумента подставим
вместо аргумента подставим 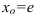 :
:
Тогда 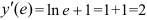 .
.
Ответ: 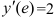 .
.
Дифференциалом функции 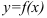 в точке
в точке  называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 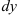 (или
(или 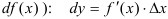 . Поскольку дифференциал независимой переменной равен приращению этой переменной:
. Поскольку дифференциал независимой переменной равен приращению этой переменной: 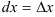 , дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной:
, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной: 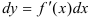 .
.
Пример 4.
Найдите дифференциал функции 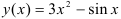 .
.
Решение:
По формуле 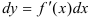 находим:
находим:
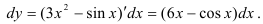
Ответ: 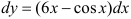 .
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
