Оглавление:
Задание: Разложение функций в ряд Маклорена.
Цель: формирование умения разлагать элементарные функции в ряд Маклорена и применять данные разложения для вычисления приближённых значений выражений.
Задание для самостоятельной внеаудиторной работы:
42.1. Выучите определение ряда Маклорена для функции. Запомните, как в этом случае будет называться функция. Разберите пример и выясните, как найти конкретный член ряда Маклорена для функции.
42.2. Ряд Маклорена для функции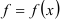 
имеет вид:
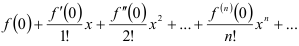Найдите:
а) третий член ряда Маклорена для функции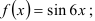 
б) четвёртый член ряда Маклорена для функции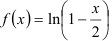 
.
42.3. Проанализируйте, при каких условиях ряд Тейлора (Маклорена) будет сходиться к порождающей функции. Выясните, какова техника разложения функции в ряд Тейлора (Маклорена). Постарайтесь освоить алгоритм, позволяющий разлагать функцию в ряд Маклорена на примере функции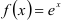 
.
42.4. Разложите функцию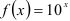 
в ряд Маклорена.
42.5. Запомните известные разложения некоторых элементарных функций в ряд Маклорена. Выясните, какие преобразования известных разложений позволяют получать новые разложения функций в ряд. Внимательно изучите технику получения подобных разложений на примере функций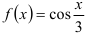 
и 
.
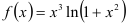42.6. Используя известное разложение в ряд Маклорена элементарных функций, представьте в виде ряда:
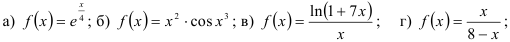
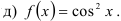
42.7. Выясните, как разложение функции в ряд Маклорена позволяет найти приближённое значение выражения.
42.8. Используя известное разложение функции в ряд Маклорена, и ограничиваясь заданным числом первых членов ряда, найдите приближённое значение выражения:
a)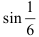 
(два первых члена ряда); б) 
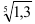(три первых члена ряда).
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Ряд для функции 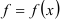в точке 
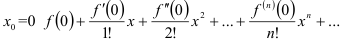называется рядом Маклорена.
Если функция 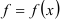имеет в точке 
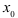производные любого порядка, то для неё можно составить ряд Маклорена. При этом функция 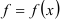называется порождающей функцией для
соответствующего ряда.
Пример 1.
Найдите третий член ряда Маклорена
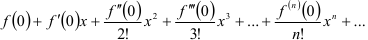для функции 
.
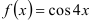Решение:
Третий член ряда Маклорена для функции 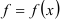имеет вид 
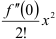. Для его нахождения вычислим вторую производную функции 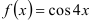в точке 
:
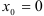1) найдём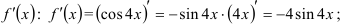 
2) найдём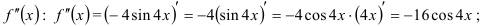 
3) найдём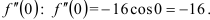 
Подставим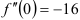 
в выражение 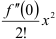, получим: 
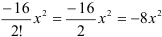. Таким образом, третий член ряда Маклорена для функции 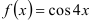равен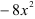 
.
Ответ: .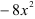
Формально ряд Тейлора (Маклорена) можно построить для любой бесконечно дифференцируемой функции 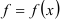в окрестности точки 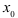. Но отсюда ещё не следует, что он будет сходиться к данной функции 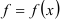. Условия, при которых ряд Тейлора (Маклорена) сходится к порождающей функции, изложены в теореме.
Теорема: Если все производные функции 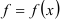ограничены в некоторой окрестности точки 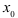(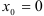) одним и тем же числом, то для любого 
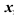из этой окрестности ряд Тейлора (Маклорена) для функции 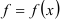сходится к данной функции, т.е. имеет место разложение
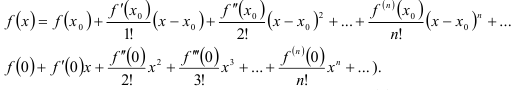
Для разложения некоторой функции 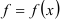в ряд Маклорена удобно использовать следующий алгоритм:
1) вычислить значения функции и всех её производных при ;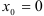
2) составить ряд Маклорена для функции :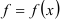
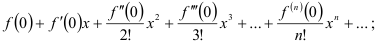
3) проверить выполнение условий теоремы о разложении функции в ряд (доказать, что все производные функции ограничены в некоторой окрестности точки 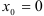одним и тем же числом);
4) записать разложение функции 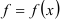в ряд Маклорена:
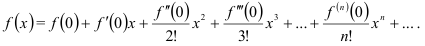
Рассматривая разложение в ряд Маклорена некоторых элементарных функций, ограничимся рядами, которые чаще всего используются на практике.
Пример 2.
Разложите функцию 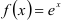в ряд Маклорена.
Решение:
Для разложения функции 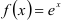в ряд Маклорена воспользуемся алгоритмом.
1) Найдём значения функции 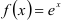и последовательно её производных в точке :
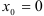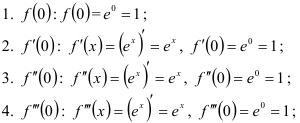
Поскольку для функции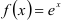 
, то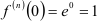 
.
2) Составим для функции 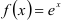ряд Маклорена, подставив найденные значения в формулу ряда Маклорена 
:
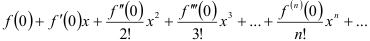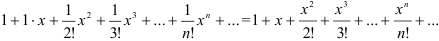
3) Проверим выполнение условий теоремы о разложении функции в ряд: для данного 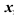найдём интервал 
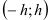, содержащий число 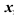, и обозначим 
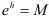. Тогда для любой производной функции имеем 
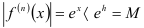. Таким образом, все производные функции 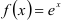в некоторой окрестности 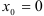ограничены одним и тем же числом 
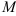. Значит, условия теоремы выполнены, и функция 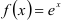может быть разложена в ряд.
4) Запишем разложение функции 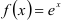в ряд Маклорена: 
.
Ответ: .
Аналогичным образом можно получить разложения в ряд Маклорена некоторых элементарных функций, которые рекомендуется запомнить:
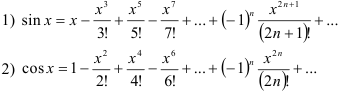
биномиальный ряд (бином Ньютона):
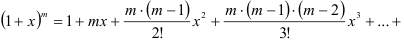
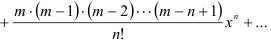
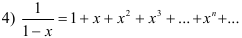
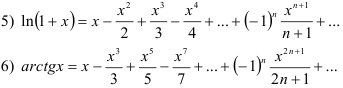
Разложение некоторых функций в ряд Маклорена можно получить, выполняя те или иные преобразования над уже имеющимися разложениями. К таким преобразованиям относятся замена переменной, сложение, вычитание, умножение, дифференцирование и интегрирование степенных рядов.
Рассмотрим примеры получения подобных разложений.
Пример 3.
Используя известные разложения, разложите в ряд Маклорена функцию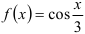 
.
Решение:
Воспользуемся известным разложением в ряд функции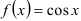 
:
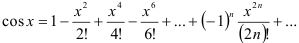
Заменим в данном разложении 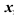на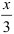 
, получим:
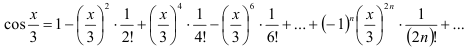
Таким образом,
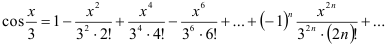
Ответ: .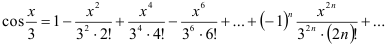
Пример 4.
Разложите в ряд Маклорена функцию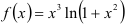 
.
Решение:
Функция 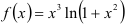представляет собой произведение 
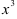на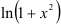 
, поэтому для её разложения в ряд Маклорена воспользуемся разложением функции 
:
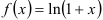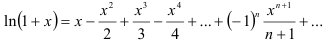
Заменим в этом разложении 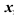на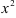 
, получим:
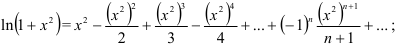
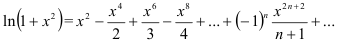
Умножим разложение 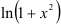на :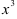
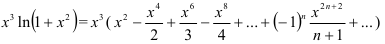
Таким образом,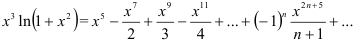 
Ответ: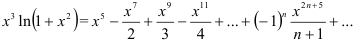
Разложение функций в ряд Маклорена находит широкое практическое применение в вопросах приближённого вычисления значений функций.
Пусть требуется вычислить значение функци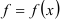и при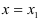 
, с заданной точностью. Если функцию 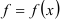в интервале 
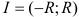можно разложить в степенной ряд 
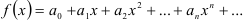, и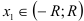 
, то точное значение 
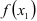равно сумме этого ряда при 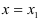, т.е. 
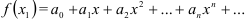, а приближённое — частичной сумме 
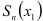, т.е. 
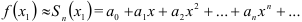. Точность этого равенства увеличивается с ростом 
.
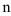Пример 5.
Найдите приближённое значение выражения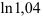 
с точностью до 0,0001, используя известные разложения функций в ряд Маклорена.
Решение:
Воспользуемся известным разложением в ряд Маклорена функции :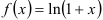 
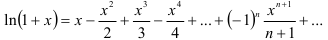Поскольку 
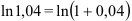, подставим в данное разложение вместо 
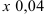, получим 
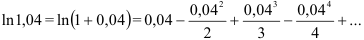Так как мы имеем знакочередующийся ряд, то при замене его суммы некоторой частичной суммой абсолютная погрешность не превышает модуля первого отброшенного члена. Непосредственной проверкой убеждаемся, что 
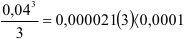, следовательно, достаточно ограничиться двумя первыми членами разложения: 
.
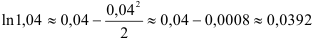Ответ: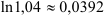 
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
