Оглавление:






Критерий устойчивости Найквиста
Первоначально разработанный Найквистом в 1932 году для изучения усилителей с отрицательной обратной связью, критерии амплитуды и фазовой устойчивости были доказаны, обобщены и впервые применены к теории автоматического управления в 1936 году. Михайлов. Критерий Найквиста Михайлова позволяет определить устойчивость замкнутой системы по типу амплитудно-фазовой АЧХ открытой системы.
Существует четкая формулировка критериев, когда открытая система стабильна и нестабильна.
В первом случае критерий устойчивости формулируется следующим образом: САР, которая стабильна в открытом состоянии, частотная характеристика разомкнутого контура открытой системы — это точка на комплексной плоскости с координатами (-1, j0) Если оно не закрыто, оно будет стабильным при закрытии. Рисунок Амплитудно-фазово-частотные характеристики: а-статические. b-Static (ν = 1)
На рисунке показаны амплитудно-фазово-частотные характеристики статической (a) и нестатической (b) систем. Амплитудно-фазовая характеристика 1 не покрывает критическую точку, поэтому система с этими характеристиками является стабильной. Система 2 нестабильна, потому что амплитудно-фазовая частотная характеристика 2 охватывает точку (-1, j0).
Амплитудно-фазово-частотная характеристика 3 проходит критическую точку. Соответствующая система находится на границе устойчивости. Рассмотрим доказательство стандартов. Передаточная функция закрытой системы, если передаточная функция системы открыта. Рассмотрим функциональность. Отношение характеристического многочлена замкнутой системы к характеристическому многочлену открытой системы. Числитель и знаменатель уравнения (20) могут быть выражены как факторы, которые являются корнями характеристического уравнения замкнутой системы.
Корень разомкнутого характеристического уравнения. Подставляя jω вместо p в последнем выражении, получается следующим образом. При изменении каждый разностный вектор числителя и знаменателя поворачивается на π2 или -π2 в зависимости от положения соответствующего маршрута.
- Предполагая, что открытая система стабильна (стабильность открытой системы часто можно определить, не рассчитывая непосредственно по системной диаграмме. Например, открытая система, которая состоит из устойчивых связей и не содержит локальной обратной связи Я знаю, что это стабильно.)
В этом случае, когда порядок характеристического уравнения с разомкнутым контуром изменяется, корень pi находится в левой полуплоскости, а аргумент C (jω) изменяется (вращение характеристического вектора с разомкнутым контуром).
Изменение аргумента D (jω) при изменении в общем случае равно числу корней в правой полуплоскости. Изменение аргумента ƒ (jω) равно разнице между изменением аргументов числителя и знаменателя. Система стабильна, когда: Вектор, когда ω изменяется от 0 до + ∞, представляет угол, равный нулю, только если годограф этого вектора не охватывает начало координат (рис. 7). Легко перейти от годографа к годографу, то есть по системе с разомкнутым контуром AFC. Фактически, выражение для может быть записано в следующем виде: — Фазовая характеристика открытой петли.
Геометрически, окончательное уравнение показано на рисунк. Рисунок Векторный годографОткрытая система ƒ (jω) AFC Следовательно, вектор ƒ (jω) годограф представляет открытую систему AFC, но сдвигает одну вправо.
Поскольку более удобно использовать амплитудно-фазовую частотную характеристику, чем векторный годограф j (jω), переместите ось ординат на один шаг вправо.
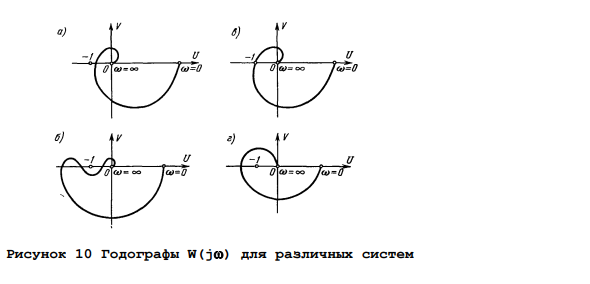
Это означает формулировку частотного случая критерия устойчивости Найквиста-Михайлова. Система автоматического управления, которая стабильна в открытом состоянии, является стабильной в закрытом состоянии, если частотная характеристика разомкнутого контура открытой системы не покрывает критическую точку. Рис. 10 Годограф W (jω) различных систем На рис. 10 показан случай так называемой абсолютно устойчивой системы. Этот термин означает, что система стабильна при уменьшении усиления разомкнутого контура.
- Напомним, что передаточная функция открытой статической системы может быть выражена. Уменьшение общего усиления k приводит к уменьшению модуля W (jω), что, как показано на рисунке 10a, не приводит к охвату точечным годографом. На рисунке 10б показан случай так называемой условно устойчивой системы. Здесь система стабильна, и общее значение усиления находится в определенных пределах.
- Как увеличение, так и уменьшение суммарного усиления k может привести к тому, что годограф охватит точки, соответствующие неустойчивости замкнутой системы. На рисунке 10в показан случай, когда система находится на устойчивой границе.
- Устойчивая граница является вибрационным типом.
Это связано с тем, что существует равенство, которое можно описать в форме на определенной частоте, когда годограф пересекает точки. Последнее уравнение является характеристическим уравнением, которое исчезает при замене p = jω. Следовательно, чисто мнимый корень является решением характеристического уравнения. На рисунке 10d показан случай нестабильной системы.
Смотрите также:
Решение задач по теории автоматического управления
| Определение устойчивости с помощью критерия гурвица | Критерий устойчивости Гурвица |
| Критерии устойчивости Михайлова | Оценка качества регулирования при гармонических воздействиях |
