Оглавление:






Кривые 2-го порядка (коники)
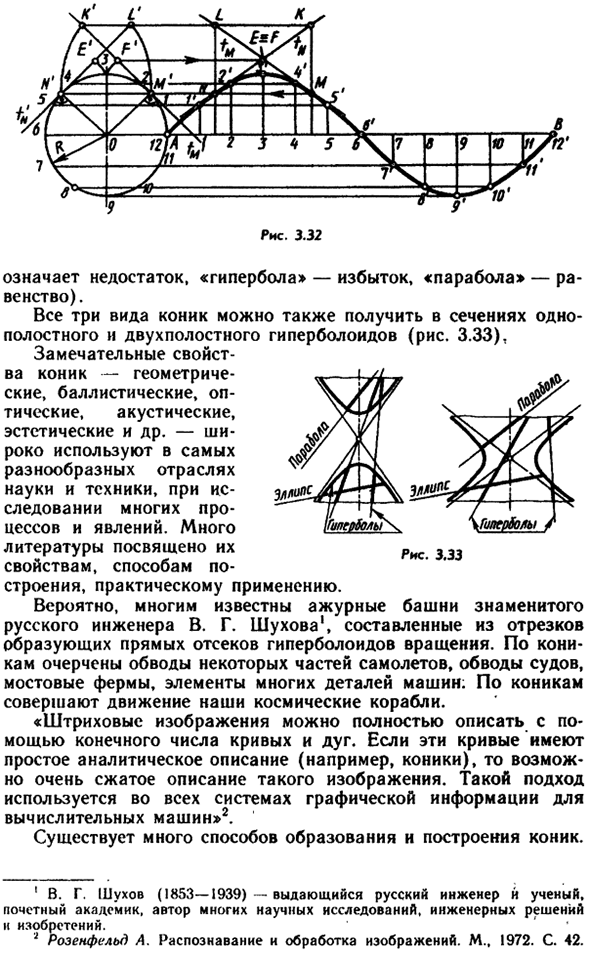
- Квадратичная кривая (коническая кривая). Открытый конус Раздел относится к Менема (4 век до нашей эры). Их теория Разработанный основательно Аполлонием Перги (3 век до нашей эры), Осмотрите плоскую часть круглого основания конуса. он Даны названия этих кривых (в переводе с греческого слова «эллипс». что 10 * Рисунок 3.32 Дефицит, «гипербола» — избыток, «парабола» — Равенство).
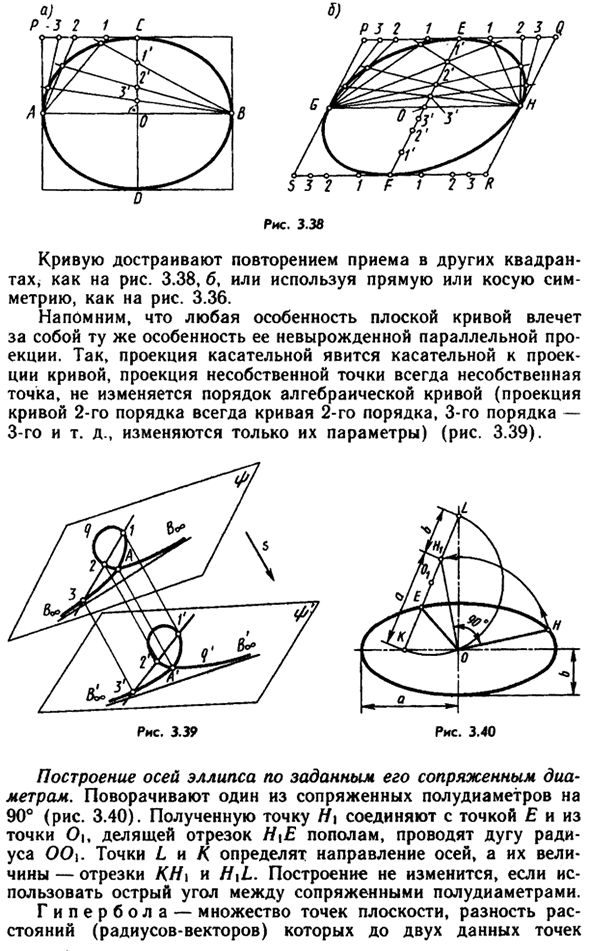
- Все три типа конических кривых могут быть получены в одном разделе. Полость и двухрезонаторный гиперболоид (рис. 3.33) т замечательный Конические свойства Геометрический, баллистический, Оптический, акустический, Эстетические и другие Широко используется в большинстве Разнообразные отрасли Наука и техника, и Много исследований Процесс и явление.
Много Литература посвящена им Свойство, метод Конструкция и практическое использование. Людмила Фирмаль
Наверное, много известных ажурных башен Русский инженер В. Г. Швов 1 состоит из сегментов Образует прямое сечение вращающегося гиперболоида. по Контур части самолета, Коник контура корабля, Мост, элемент многих деталей машин: конус Переместить космический корабль. «Линия искусства Используйте конечное число кривых и дуг.
Эти кривые Простое аналитическое описание (например, коническое), затем Вероятно, очень краткое описание такого изображения. Такой подход Используется во всех графических информационных системах Компьютер «2. Есть много способов сформировать и построить коническую кривую. Рисунок 3.33 1 В. Г. Швов (1853-1939) — выдающийся русский инженер и ученый.
Почетная академия, автор многих научных исследований, технических решений И изобретение. 2 Розенфельд А. Распознавание и обработка изображений. М., 1972.П. 42. 63 Рисунок 3.34 Рисунок 3.35 Их можно рассматривать как прямые, полученные сечением Плоскость конуса второго порядка, как и многие точки на плоскости Координаты удовлетворяют второму заданному уравнению Как проекция круга степени.
Как полученная кривая Пересечение двух проекционных линий (проекция Образование); как локус точек, линий, кругов, Делать определенные движения (кинематика) Образование); как конверт. Выбор метода формирования, Поэтому структура зависит от условий задачи. Эллипс-множество точек на плоскости, сумма расстояний (Радиус-вектор) до 2 баллов каждый 1 в одной плоскости (фокус) является постоянной (равной 2a-длинная ось эллипса).
С этим свойством Фокус, структура эллипса основана на большом случае Топоры и хитрости (рис. 3.34). Краткое изложение некоторых пунктов /, 2, 3, … Из центра эллипса О и одного из координационных центров, F \ Расходы На дуге радиуса A1 и на пересечении дуги радиуса / B от F * Получите две точки эллипса M и M . Тогда F \ arc Вырезать из f с дугой радиуса A2 и радиусом 2BU Точки L и L \ и т. Д.
Точки N и N \ настроены как точки симметрии. M и Mg для оси эллипса. Вытащите арк-трюк Получить маленькие вершины C и D на пересечении радиуса a Ось эллипса. Если указана ось эллипса, трюк определяется как Пересечение с большой осью дуги /? = Чертеж из C Или Д. Эллиптические канонические уравнения относятся к этой оси. Имеет форму U2 I2 На основе непрерывного фокуса на основе эллипса.
Постройте эллипс, используя нити одинаковой длины Длинная ось (простейший эллипсограф (рис. 3.35) 2. От 1 крысы Фокус-огонь, фокус. Этот метод построения эллипса описан в «Compasss and Ряд «, Петр I в 1709 году Если вы перемещаете кончик карандаша, потянув за нить Состояние, она рисует половину эллипса. Хорошо и Вы можете получить эллипс как кончик нити и карандаш, Очень близко к эллипсу, указанному аналитически.
Как правило, он основан на нескольких эллипсографах. Самый простой способ создать эллипс — это использовать концентрические круги. Окружность построена на оси как диаметр (рис. 3.36). Если углы луча равны или неравны И через пересечение с большим кругом Прямая и маленький круг, параллельный малой оси Параллельно главной оси.
Их пересечение является эллипсом. здесь Полезно для определения ординаты эллипса Абсцисса и наоборот. Он основан на втором открытии Ось эллипса вдоль определенного эллипса большая (рис. 3.37, а) или Малый (рис. 3.37, б) одна из его точек М широко используется На самом деле. Ход строительства обозначен стрелками.
Рисунок 3.38 и конфигурация данного эллипса Использует два проекционных луча от оси, точка А Разделить B и стороны прямоугольника и прямоугольника на равные части (Или в той же точке, Дополнительная точка эллипса с изменяющейся кривизной Более резко). Рисунок 3.38, б-параллельная проекция 3.38, а. ось Эллипс проецируется на диаметр сопряжения, Прямоугольный — параллелограмм.
- Вы можете нарисовать пачку с края От малой оси и, следовательно, сопряженного конца Диаметр. s- 65 Рисунок 3.38 Кривая завершается повторением приема в других квадрантах. тах; 3.38,6, как показано, или используйте прямую или диагональную Симметрия как показано. 3,36. Особая точка плоской кривой За этим стоит та же особенность невырожденного параллелизма Проекция.
Следовательно, касательная проекция Кривая проекция, неуместная точечная проекция всегда неуместна Порядок точек и алгебраических кривых не меняется (проекция Квадратичная кривая всегда является квадратичной или кубической Изменяются только параметры, например третий (рисунок 3.39). Рисунок 3.39 Рисунок 3.40
Построить ось эллипса с указанным сопряженным Диаметр. Людмила Фирмаль
Один из парных радиусов 90 ° (рис. 3.40). Результирующая точка H \ связана с точкой ξ, Точка 0 | Разделить отрезок H \ E пополам и нарисовать дугу Радиус 00 . Точки L и K определяют направление оси, Количество KH {и H \ L сегмент. Структура не меняется, если Используйте острый угол между парными радиусами. Гипербола-множество точек на плоскости, разность Расстояние до двух заданных точек (радиус-вектор) 66 к2 рт.ст.
Рисунок ЗМ Рисунок 3.42 Постоянное значение (равное той же плоскости (фокус) 2а — действительная ось гиперболы, рис. 3.41). Об этой характеристике гиперболической точки, называемой фокусной, Гиперболическая конструкция основана на реальном времени Оси и хитрости. Точка f, 2, <? , … замечено (рисунок 3.42) и постепенно увеличивается Проведите расстояние между ними и не в фокусе Fi Fi Сегмент B /, B2, от радиуса, равного сегменту AJy A2U …, и F% …
Пересечения дуг At и B /, A2 и B2 и т. Д. Являются гиперболическими точками. Построить левую ветку Кривая из точки F2 расходов Дуги с радиусами от At, / 42, … и Fi- Радиус B /, B2, …, но это возможно Осевой или Центральная симметрия На чертеже. Мнимая ось CD и \ А * асимптоты встроены в один Из техники, показанной в Верхняя и нижняя часть рисунка 3.43.
Трюк, если указана только ось Определено на пересечении Описанный круг Построен на прямоугольной оси, Используйте ОСь X. Рисунок 3.43 Гиперболическая конструкция ею Точка М и асимптотика. Проведите параллельные линии через точку М Любой радиус, такой как асимптота и гипербола 01, 02 (Рисунок 3.44, а) Пересечение этих параллелей.
Строительная точка Гипербола обозначена стрелкой на чертеже. Когда прогнозируется Рисунок 3.44 и пл. Пирог не параллелен мне, тогда мы получаем рис. 3.44, б. Так что эта структура все Угол между асимптотами. Теперь вы можете построить ее трюк И мнимая ось (см. Рис. 3.43). При необходимости вторая ветка 3 * 67 / Асимптот Рисунок 3.44 Гипербола построена как центрально-симметричная структура, Используя его диаметр.
Эта технология широко используется в технике, особенно в следующих случаях: Создать диаграмму индикатора теплового двигателя. Парабола — это набор точек на плоскости, Равное расстояние от точки (фокус) и прямой (руководство, справочник) Они находятся в одной плоскости (рис. 3.45). р значение- Расстояние между фокусом и направляющим параметром Парабола.
Построение параболы из заданного Фокус F и руководство (рис. 3.46). Через фокус Проведите основной диаметр (ось) параболы вертикально Направляющая Сегмент HF разделен пополам и найден пик A Парабола. На правой оси точки А некоторые Случайно выбранные точки, вспомогательные.
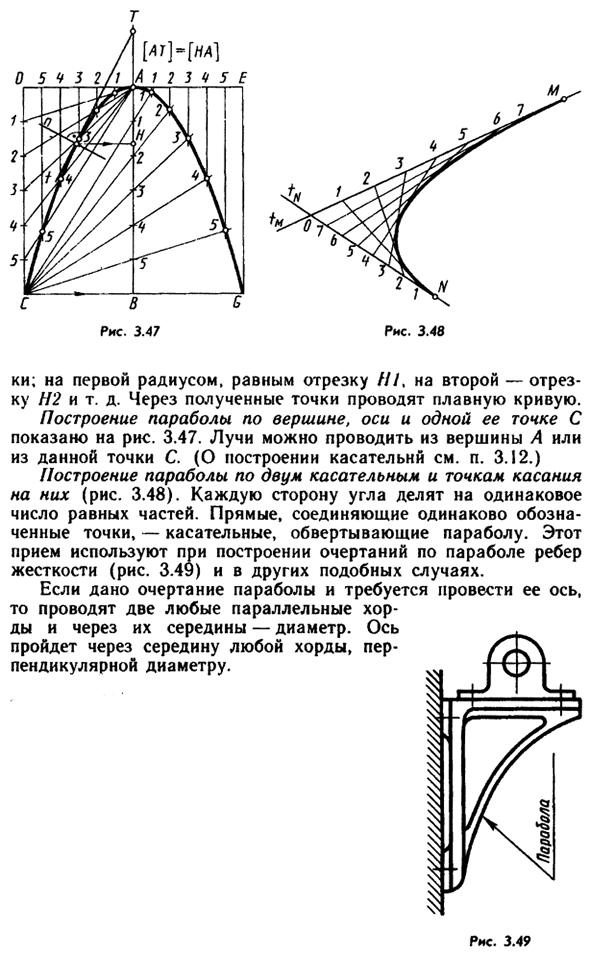
Прямая линия, вертикальная ось и d Расфокусировать F-вырез d Мэриленд ■ < N «D в \ (Для р 2 р 0,2 • J » MF ~ W ~ 1 К ^ L ^ 4ss ^ = 7 > Это. 3,45 68 T ki; первый радиус равен сегменту ///, второй is- Сегмент Н2 и т. Д. Гладкая кривая проведена через полученные точки. Построить параболу в вершине, оси и одной из ее точек C Показано на рисунке. 3,47. Луч — это пик А или Из заданной точки C (для построения касательных см. §3.12).
Создайте параболу из двух касательных и контакта Они (рис. 3.48). Каждая сторона угла разделена поровну Количество равных частей. Прямо, равномерно связано Указанная точка представляет собой касательную, которая обволакивает параболу.
Это Этот метод используется при создании параболических контуров для ребер Жесткость (рис. 3.49) и другие подобные случаи. Учитывая контур параболы и ее ось необходима, Затем проведите любые два параллельно Диаметр через аккорд и его середину. ось Через середину аккорда Перпендикулярно диаметру.
Смотрите также:
| Некоторые плоские кривые, наиболее часто встречающиеся в практике | Построение касательной и нормали к конике |
| Спирали | Круги кривизны коник |
