Пусть 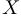 — некоторое множество, состоящее из
— некоторое множество, состоящее из 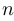 элементов, и
элементов, и 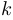 — некоторое целое неотрицательное число, не превосходящее
— некоторое целое неотрицательное число, не превосходящее 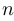 . Мы хотим выяснить, каково число тех подмножеств множества
. Мы хотим выяснить, каково число тех подмножеств множества 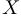 , которые имеют ровно
, которые имеют ровно 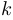 элементов.
элементов.
Это число играет важную роль не только в теории вероятностей, но и в математике вообще. Оно называется числом сочетаний из 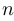 элементов по
элементов по 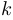 или биномиальным коэффициентом. Иногда его называют также числом Паскаля. Обозначается оно через
или биномиальным коэффициентом. Иногда его называют также числом Паскаля. Обозначается оно через 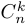 .
.
Простейшие свойства и некоторые значения числа 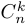 можно получить непосредственно из определения. Например:
можно получить непосредственно из определения. Например:
1. 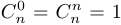 , поскольку существует ровно одно подмножество, не имеющее ни одного элемента (пустое подмножество), и существует ровно одно подмножество, имеющее
, поскольку существует ровно одно подмножество, не имеющее ни одного элемента (пустое подмножество), и существует ровно одно подмножество, имеющее 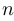 элементов (само множество
элементов (само множество 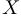 ).
).
2. 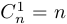 , поскольку в
, поскольку в  существует ровно
существует ровно  элементов, которые и являются одноточечными подмножествами.
элементов, которые и являются одноточечными подмножествами.
3. 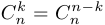 . Это свойство называется симметрией биномиальных коэффициентов. Чтобы понять, откуда оно возникло, представим себе, что мы «убрали» из
. Это свойство называется симметрией биномиальных коэффициентов. Чтобы понять, откуда оно возникло, представим себе, что мы «убрали» из 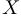 некоторое подмножество, состоящее из
некоторое подмножество, состоящее из 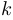 элементов. Осталось дополнение, содержащее
элементов. Осталось дополнение, содержащее  элементов. Если уберем другое подмножество, содержащее также
элементов. Если уберем другое подмножество, содержащее также 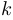 элементов, то и дополнение будет другим, содержащим
элементов, то и дополнение будет другим, содержащим  элементов. Таким образом, число
элементов. Таким образом, число 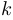 -элементных множеств совпадает с числом
-элементных множеств совпадает с числом  -элементных множеств, что и означает симметрию.
-элементных множеств, что и означает симметрию.
Отсюда, в частности, следует, что 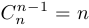 .
.
4. 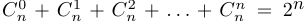 . Действительно, слева написана сумма чисел всех подмножеств с числом элементов, равным
. Действительно, слева написана сумма чисел всех подмножеств с числом элементов, равным , то есть число всех подмножеств вообще, которое равно
, то есть число всех подмножеств вообще, которое равно 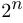 .
.
Для того чтобы получить другие свойства и значения чисел 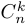 , рассмотрим, как выглядят разложения степени
, рассмотрим, как выглядят разложения степени 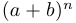 при конкретных значениях
при конкретных значениях 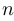 :
:
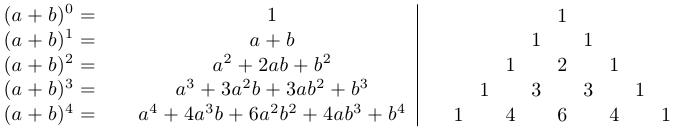
Справа от черты мы выписали таблицу коэффициентов соответствующих разложений бинома. Эта таблица называется треугольником Паскаля, а элементы этой таблицы и есть числа Паскаля, или биномиальные коэффициенты.
Можно догадаться, как строится таблица коэффициентов: крайние элементы в таблице равны 1, а каждый «внутренний» элемент равен сумме двух вышестоящих, ближайших к нему. Зная это правило, напишем еще одну строку в таблице.
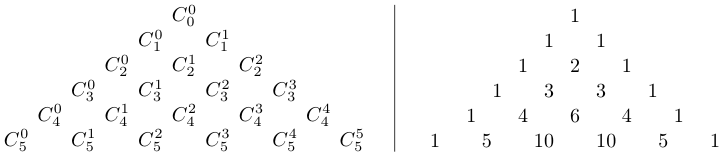
Слева от черты мы выписали обозначения соответствующих коэффициентов. Эти обозначения используются и в знаменитой формуле бинома Ньютона:
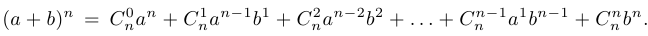
Чтобы понять, что биномиальные коэффициенты имеют прямое отношение к числу подмножеств данного конечного множества, представим 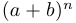 в виде произведения
в виде произведения 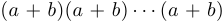 и мысленно перемножим скобки. После перемножения и до приведения подобных членов в общей получившейся сумме будет несколько одинаковых слагаемых вида
и мысленно перемножим скобки. После перемножения и до приведения подобных членов в общей получившейся сумме будет несколько одинаковых слагаемых вида 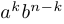 .
.
Количество этих слагаемых равно числу способов, которыми мы можем из всех скобок выбрать 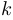 таких, которые соответствуют выбору
таких, которые соответствуют выбору 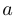 при перемножении. В остальных скобках мы выбираем
при перемножении. В остальных скобках мы выбираем 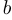 . Это и означает, что мы из всего множества
. Это и означает, что мы из всего множества 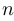 скобок выбираем всевозможные
скобок выбираем всевозможные 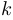 -элементные подмножества.
-элементные подмножества.
Мы доказали, что число сочетаний совпадает с соответствующим коэффициентом в биноме Ньютона.
Факториал.
Для того чтобы выписать общую формулу для числа сочетаний, нам понадобится достаточно простое и часто используемое понятие. Факториалом 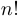 натурального числа
натурального числа 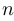 называется произведение всех натуральных чисел, не превосходящих
называется произведение всех натуральных чисел, не превосходящих 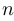 . По договоренности считается, что
. По договоренности считается, что 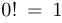 . Таким образом,
. Таким образом, 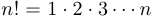 .
.
Примеры: 
Отметим, что факториалы очень быстро «нарастают», например при 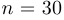 образуется число, содержащее 33 знака.
образуется число, содержащее 33 знака.
Оказывается, что 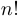 в точности равен числу способов, которыми можно расположить
в точности равен числу способов, которыми можно расположить 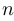 элементов (составить список, в котором был бы важен порядок), или, другими словами, числу перестановок из
элементов (составить список, в котором был бы важен порядок), или, другими словами, числу перестановок из 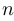 элементов. Перестановкой из
элементов. Перестановкой из 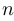 элементов называется любой упорядоченный набор этих элементов. Число всех перестановок из
элементов называется любой упорядоченный набор этих элементов. Число всех перестановок из 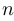 элементов равно
элементов равно 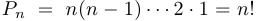 .
.
Используя понятие перестановки, мы можем получить явную формулу для числа сочетаний. Действительно, отделим мысленно группу в 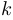 элементов из общего набора, состоящего из
элементов из общего набора, состоящего из 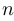 элементов. После перестановок в общем наборе мы должны отождествить те из них, которые лишь переставляют элементы внутри отделенной группы (таких будет
элементов. После перестановок в общем наборе мы должны отождествить те из них, которые лишь переставляют элементы внутри отделенной группы (таких будет 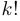 штук), а затем те из них, которые лишь переставляют элементы в дополнительном множестве (таких будет
штук), а затем те из них, которые лишь переставляют элементы в дополнительном множестве (таких будет 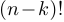 штук).
штук).
Таким образом, 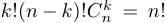 , откуда следует формула для числа сочетаний:
, откуда следует формула для числа сочетаний:
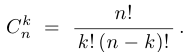
Заметим, что, несмотря на то что выражение, определяющее биномиальный коэффициент, дробное, результат, в силу самого определения числа сочетаний, является целым числом.
Примеры: 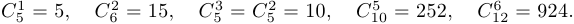
Практическое вычисление числа сочетаний. Заметим, что вычисление биномиальных коэффициентов на калькуляторе или компьютере затруднительно из-за быстрого нарастания факториалов, и в связи с этим рекомендуется, прежде чем переходить к практическому вычислению, выписать соответствующие произведения и, насколько возможно, упростить дроби.
Примеры. 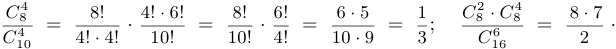
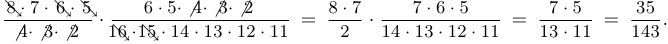
Разумеется, подобный подход осуществим далеко не всегда. Иногда при вычислении громоздких выражений полезно их прологарифмировать или использовать приближенную формулу Стирлинга:
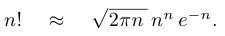
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: логические функции |
| Курсовая работа на тему: метод математической индукции |
| Курсовая работа на тему: числовые последовательности |
| Курсовая работа на тему: предел функции |
