Математическая постановка задачи линейного программирования
Из рассмотрения задач математического программирования следует, что в общем виде решить их практически невозможно. Целесообразно рассматривать отдельные классы (виды) задач. Для каждого такого класса удается сформулировать алгоритм решения, приемлемый только для данного класса задач. Наиболее разработанными в математическом программировании являются задачи линейного программирования.
Целевая функция в них линейна, а условия-ограничения содержат линейные равенства и линейные неравенства. Переменные могут быть подчинены или не подчинены требованию неотрицательности. Примерами задач линейного программирования являются уже сформулированные в гл. I задача о питании, транспортная задача и т.п. Одна и та же задача линейного программирования может быть записана в различной форме. Говорят, что задача линейного программирования записана в канонической форме, если все ее ограничения, кроме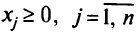 
, представляют собой равенства. Если все ограничения имеют вид неравенств, то задача записана в стандартной форме.
Для записи задачи линейного программирования в различной форме применяются следующие приемы.
- Точка минимума функции
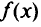, совпадающая с точкой максимума функции —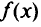. - Ограничения в виде неравенств
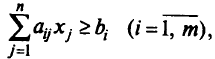
можно представить в виде равенств, использовав новые переменные
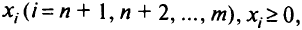
называемые слабыми:
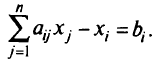
Для неравенства
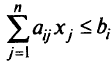
можно взять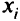 
и получить равенство
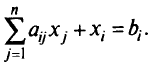
Ограничение в виде равенства
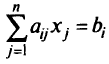
можно заменить двумя неравенствами:
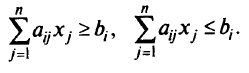
Если имеется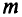 
равенств
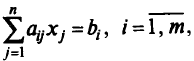
их можно заменить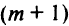 
неравенствами
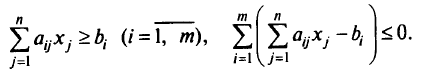
Если на переменную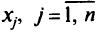 
, и , не наложено условие неотрицательности, ее можно заменить двумя неотрицательными переменными 
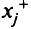и 
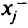, положив 
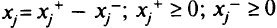. Если имеется 
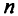таких переменных 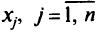, то их можно заменить 
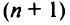неотрицательными переменным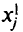и 
и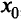 
, положив 
.
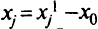Система офаничений в виде равенств и неравенств образует выпуклое множество — выпуклый многогранник. Это множество может быть ограниченным и неограниченным. Целевая функция задачи линейного программирования — тоже выпуклая функция. Таким образом, задача линейного программирования является частным случаем задачи выпуклого программирования.
Рассмотрим систему ограничений задачи линейного программирования в виде равенств
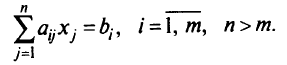
Говорят, что система (2.1) линейных уравнений совместна, если она имеет, по крайней мере, одно решение. Система (2.1) называется избыточной, если одно из уравнений можно выразить в виде линейной комбинации остальных. Система (2.1) несовместна, если ранг матрицы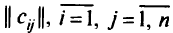 
равен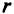 
, ранг расширенной матрицы этой системы (с присоединенным столбцом 
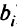) больше 
.
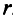В системе (2.1) число переменных (неизвестных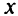 
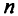) больше числа уравнений 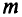. Будем считать, что ранг этой системы равен 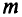(система неизбыточна) и что система (2.1) совместна. Тогда 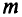переменных из общего их числа образуют базисные переменные, а остальные 
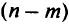переменных называют свободными. Система (2.1) в этом случае будет иметь бесчисленное множество решений, так как свободным переменным можно давать любые значения, для которых находят значения базисных переменных.
Решение системы (2.1) называют базисным, если все свободные переменные равны нулю. Если система уравнений имеет решение, то она имеет и базисное решение. Решение системы уравнений (2.1) называют допустимым, если все его компоненты неотрицательны. Если система линейных уравнений обладает допустимым решением, то она имеет и базисное допустимое решение. Совокупность всех допустимых решений системы (2.1) есть выпуклое множество или, другими словами, множество решений задачи линейного программирования выпукло. Так как это множество образовано плоскостями (гиперплоскостями), то оно имеет вид выпуклого многогранника. Базисное допустимое решение соответствует крайней точке выпуклого многогранника (его грани или вершине).
Если существует оптимальное решение задачи линейного программирования, то существует базисное оптимальное решение.
Целевая функция задачи линейного программирования есть уравнение плоскости (или гиперплоскости для числа переменных больше трех). Пусть в вершинах выпуклого многоугольника мы установили «столбы», высота которых определяет значения целевой функции в данной вершине. На эти «столбы» наложим плоскость (графическое представление целевой функции). Очевидно, что максимальное и минимальное значения целевая функция задачи линейного программирования достигает либо в вершине выпуклого многогранника, либо на одной из его граней. Таким образом, решение (решения) задачи линейного программирования лежит в вершинах выпуклого многогранника и для его нахождения надо вычислить значения целевой функции в вершинах выпуклого многогранника, определяемого условиями-ограничениями задачи.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
