Оглавление:
Метод «от частного к общему»
Среди конкурсных задач иногда встречаются такие (обычно они содержат параметр или несколько неизвестных), для решения которых вначале, исходя из условий задачи, делается вывод, что искомая величина (величины) должна удовлетворять, в частности, некоторому, вообще говоря, более слабому по сравнению с исходными, условию. Затем отбираются все возможные значения искомой величины, удовлетворяющие этому условию. При этом, по-сути, осуществляется переход к следствию. В конце делается обязательная полная проверка исходных условий задачи для всех найденных решений.
Назовём приведённый подход к решению задач «методом от частного к общему», поскольку суть метода состоит в том, что вначале отбираются все решения, удовлетворяющие частному условию, а последующая проверка позволяет отсечь все посторонние решения, и, таким образом, определить (общее) решение задачи. Рассмотрим две наиболее часто встречающиеся разновидности задач, решаемых этим методом.
Пусть, например, требуется найти все значения 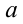 и
и 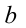 , при которых некоторое условие
, при которых некоторое условие 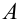 , зависящее от величин
, зависящее от величин 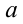 ,
, 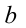 и
и 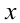 , должно выполняться сразу при всех значениях
, должно выполняться сразу при всех значениях 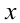 принадлежащих заданному бесконечному множеству
принадлежащих заданному бесконечному множеству 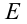 (иногда подобные задачи решаются также методом неопределённых коэффициентов).
(иногда подобные задачи решаются также методом неопределённых коэффициентов).
Поскольку условие 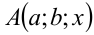 должно выполняться сразу при всех значениях
должно выполняться сразу при всех значениях 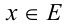 то можно подставить вместо
то можно подставить вместо 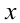 отдельные частные значения
отдельные частные значения 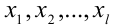 из
из 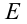 (их вид и количество выбирают из соображений целесообразности и удобства). Иногда этого бывает достаточно, чтобы, решив полученную систему условий
(их вид и количество выбирают из соображений целесообразности и удобства). Иногда этого бывает достаточно, чтобы, решив полученную систему условий

найти из неё все возможные значения 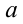 ,
,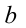 , а затем сделать их проверку. Проверка в данном случае обязательна, поскольку множество
, а затем сделать их проверку. Проверка в данном случае обязательна, поскольку множество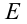 бесконечно, и все значения
бесконечно, и все значения 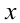 подставить невозможно, а подстановка каждого очередного значения
подставить невозможно, а подстановка каждого очередного значения 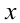 приво-дит к возникновению ещё одного ограничения на значения
приво-дит к возникновению ещё одного ограничения на значения 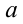 и
и 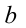 . Таким образом, множество первоначально найденных значений
. Таким образом, множество первоначально найденных значений 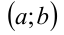 может впоследствии лишь сужаться, и в конечном итоге таких значений
может впоследствии лишь сужаться, и в конечном итоге таких значений 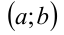 которые бы удовлетворяли условию
которые бы удовлетворяли условию 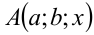 при всех
при всех 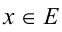 , может не оказаться вовсе. Иными словами, полученная система условий (1) является набором необходимых, но не достаточных требований к
, может не оказаться вовсе. Иными словами, полученная система условий (1) является набором необходимых, но не достаточных требований к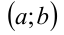 в исходной задаче (т.е. если
в исходной задаче (т.е. если 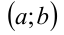 удовлетворяют условиям задачи, то они удовлетворяют и системе (1).
удовлетворяют условиям задачи, то они удовлетворяют и системе (1).
Обратное утверждение о том, что если 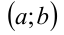 удовлетворяют системе (1), то они удовлетворяют условиям задачи, вообще говоря, неверно, и именно это подлежит проверке.)
удовлетворяют системе (1), то они удовлетворяют условиям задачи, вообще говоря, неверно, и именно это подлежит проверке.)
Пример №359.
Найти такие числа 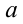 и
и 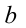 , что при всех
, что при всех 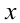 справедливо равенство
справедливо равенство
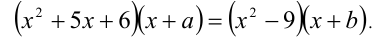
Решение:
Разложим квадратичные выражения в обеих частях уравнения на линейные множители:
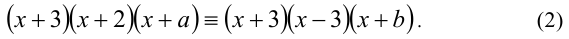
Поскольку, по условию, данное равенство должно выполняться сразу при всех действительных значениях 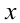 , то, в частности, оно должно выполняться и при
, то, в частности, оно должно выполняться и при 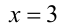 и
и 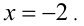 Подставляя эти значения в равенство, приходим к системе двух линейных уравнений относительно
Подставляя эти значения в равенство, приходим к системе двух линейных уравнений относительно 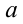 и
и 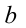 :
:
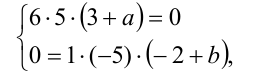
решая которую, находим 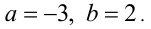 Для проверки подставим найденную пару
Для проверки подставим найденную пару 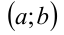 в равенство (2):
в равенство (2): 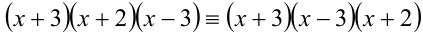 -верно при всех
-верно при всех 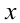 . Ответ:
. Ответ: 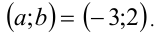
Пример №360.
Найти все пары 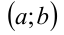 такие, что равенство
такие, что равенство 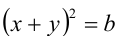 выполняется при всех
выполняется при всех 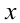 ,
, 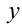 , удовлетворяющих условию
, удовлетворяющих условию 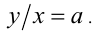
Решение:
Заметим, например, что пары чисел 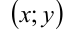 вида
вида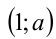 и
и 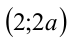 удовлетворяют условию
удовлетворяют условию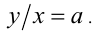 . Подставим их в равенство
. Подставим их в равенство 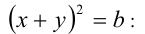
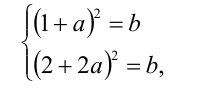
откуда имеем 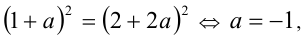 тогда
тогда 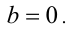
Проверкой убеждаемся, что для единственной найденной пары 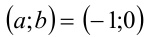 равенство
равенство 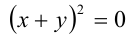 действительно выполняется при всех
действительно выполняется при всех 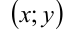 таких, что
таких, что 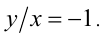 Ответ:
Ответ: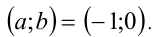
2.Близкими (по методу решения) к задачам рассмотренной выше группы являются некоторые из задач типа: «Найти все значения параметра, при которых уравнение (неравенство, система) имеет единственное решение». Например, в задачах с одной неизвестной 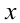 (при условии единственности решения) обнаруживается, что наряду с
(при условии единственности решения) обнаруживается, что наряду с 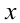 число
число 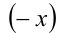 (или
(или 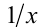 и т.д.) также удовлетворяет условиям задачи, а поэтому они должны совпадать. Отсюда находится, что
и т.д.) также удовлетворяет условиям задачи, а поэтому они должны совпадать. Отсюда находится, что 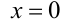 , подставляется в исходное условие, и определяются искомые значения параметров, которые в конце проверяются.
, подставляется в исходное условие, и определяются искомые значения параметров, которые в конце проверяются.
Пример №361.
При каких значениях 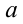 неравенство
неравенство
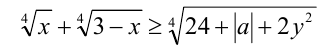
имеет единственное решение?
Решение:
ОДЗ: 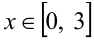 . Обозначим через
. Обозначим через 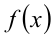 и
и 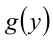 функции в левой и в правой частях неравенства соответственно. Во-первых, так как
функции в левой и в правой частях неравенства соответственно. Во-первых, так как 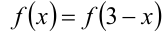 , то наряду с решением
, то наряду с решением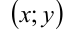 пара
пара 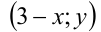 также будет решением данного неравенства. Поэтому необходимым условием единственности решения является требование
также будет решением данного неравенства. Поэтому необходимым условием единственности решения является требование 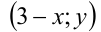 т.е.
т.е. 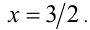 Во-вторых, так как
Во-вторых, так как 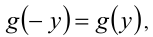 то наряду с решением
то наряду с решением 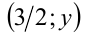 неравенство имеет решение
неравенство имеет решение 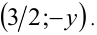 Поэтому для единственности решения необходимо, чтобы
Поэтому для единственности решения необходимо, чтобы 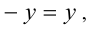 т.е
т.е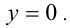 Итак, если решение единственно, то это
Итак, если решение единственно, то это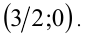 Найдём
Найдём 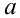 , для этого подставим
, для этого подставим 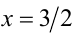 и
и 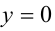 в исходное неравенство:
в исходное неравенство: 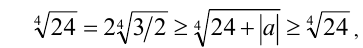 следовательно,
следовательно, 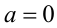 .
.
Проверка 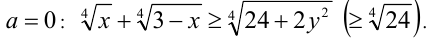 Найдём наибольшее значение функции
Найдём наибольшее значение функции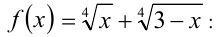
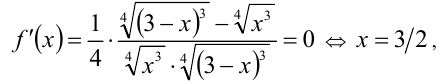
причем на отрезке 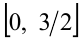 функция
функция 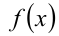 возрастает, а на отрезке
возрастает, а на отрезке 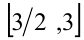 убывает, достигая в точке
убывает, достигая в точке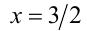 своего наибольшего значения
своего наибольшего значения 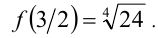 Значит,
Значит, 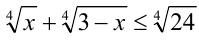 и неравенство выполняется тогда и только тогда, когда
и неравенство выполняется тогда и только тогда, когда
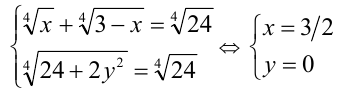 — единственное решение. Ответ:
— единственное решение. Ответ: 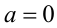 .
.
Пример №362.
Найти все 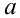 , при которых система неравенств
, при которых система неравенств
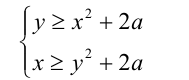
имеет единственное решение.
Решение:
Заметим, что если 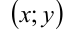 — решение системы, то пара чисел
— решение системы, то пара чисел 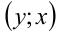 также будет решением системы, поэтому необходимым условием единственности решения является требование
также будет решением системы, поэтому необходимым условием единственности решения является требование 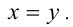 Подставляя в систему, получим неравенство
Подставляя в систему, получим неравенство 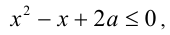 которое имеет единственное решение
которое имеет единственное решение 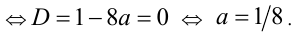 Для проверки найденного значения параметра подставим его в исходную систему и проверим, будет ли она иметь единственное решение:
Для проверки найденного значения параметра подставим его в исходную систему и проверим, будет ли она иметь единственное решение:
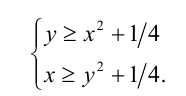
Складывая неравенства системы, получим неравенство
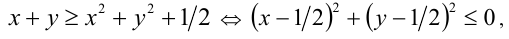
которое имеет единственное решение 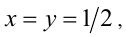 удовлетворяющее системе. Ответ:
удовлетворяющее системе. Ответ: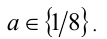
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
