Оглавление:







Метод последовательных приближений
- Интегрирование нелинейных дифференциальных уравнений вынужденных колебаний может быть выполнено с использованием метода аппроксимации последовательного приближения. Большое количество экспериментов и наблюдений за работой оборудования, выполняющего нелинейные вынужденные колебания, свидетельствуют о наличии периодических движений в установившемся состоянии. Поэтому, применяя метод последовательного приближения, получаем периодическое решение круговой частоты, равной круговой частоте возмущенной силы. Поясним идею этого метода на примере дифференциального уравнения Я к Х ПФ х 4-ч греха пт. Здесь p. и w-малый параметр, f x -непрерывная нелинейная нечетная функция x.
В качестве начального приближения опустите нелинейное частное pf x этого уравнения, чтобы найти конкретное решение xa соответствующего линейного дифференциального уравнения. Д Л Х1 L81pr. Легко увидеть решение х а sinpi Удовлетворяют этому уравнению. Затем назначьте полученное значение xt нелинейной функции p x , чтобы найти 2-е приближение x .То есть мы вычисляем дифференциальное уравнение, а затем интегрируем его. Н2 А ХД ПФ х, ч греха пт. После решения этого уравнения определите 2-е приближение Си Б2 греха пт БС грех 3 ПТ В8 грех 5пт — -… если мы введем xa в нелинейную функцию p x , то есть вычислим p xa , то найдем 3-е приближение xa. Вы можете получить его, интегрируя уравнения.
Гак как материальная система состоит из конуса и двух грузов, то момент инерции системы равен сумме моментов инерции конуса и грузов. Людмила Фирмаль
Определяются и последующие приближения. Ниже приведена последовательность, которая решает задачу с вынужденными колебаниями в нелинейных системах с использованием слегка модифицированного метода Даффинга. она основана на методе последовательного приближения. О. Дуффинга, Erzwungene СЧ Wingen беи veranderlicher Eigenfrequenz УНД jhaltechne BedeQtung, Брауншвейг 1918. 1 Создать дифференциальное уравнение для вынужденных колебаний нелинейной системы Х к Х х фут греха пт gvl p и ft-малые параметры, а f x — непрерывная нелинейная функция, x.
Здесь мы рассмотрим случай, когда x -нечетная функция, т. е. — x — x , а проекция возмущенной силы-ft sin p. 2 Определите первое приближение xx. предположим q 0.То есть интегрируем линейное уравнение X A x ftsinpf. когда xf принимает личное решение Х1 a1sinpf Здесь коэффициент ah подлежит последующему определению. 3 Добавить термин p X в левую и правую части уравнения в пункте 1 и записать его в следующем формате Х р2х П — А х р х фут греха пт -. 4 чтобы определить 2-е приближение x2, вставьте значение x1 a1sinp P. 2 p.
В правую часть уравнения, т. е. Х п х па-АА Си является cxi обладает фут греха пт 5 использовать простейшее выражение для выражения нечетной функции Xi f in sin pt в виде тригонометрического ряда 2 isin pZ. In другими словами, xj A. sin p , где 1, 3, 5 6 ввести этот результат в дифференциальное уравнение пункта 4 и представить в виде Х х п р -а а — -в формате pxi фут грех Пи щ х, грех ИПТ Где 1 3, 5,…
В связи с нахождением периодического решения этого уравнения возьмем коэффициент, равный нулю в sin pt и решим уравнение p1-Aa aj plj — — ft 0 для определения значения ai p2-A8 ax Ai 0-0 равно 1 от удельного решения производной Уравнение в предыдущем абзаце бесконечно увеличивается в соответствии с законом — a 1 1- — в T cos pt искомое решение является апериодическим 8 при условии p -Aa ax pL1 — — A 0 отличается Пункт 6 социальные уравнения принимают вид −5 Р2х p2M1p ПЛ Здесь. 1 3 5 7…Интегрируем это уравнение и находим 2-е приближение х, ВХ греха пт БС грех 3 ПТ В6 5пф…
Где первый член bx sin pt является общим решением соответствующего однородного уравнения p2×0, а все остальные члены являются частными решениями этого неоднородного уравнения. 9 после дуффинга, коэффициенты B и A коэффициентов 2-го приближения первой пункт 2 и пункт 8 греха Пи сделать постоянный эквивалент. дя грех п БС греха 3 РФ бб грех 5П Здесь ai определяется в 7. 10 xt-определяет 3-е и последующие приближения в соответствии с набором вычислений, описанных в п. 4 −9. Метод непрерывной аппроксимации дуффинга является одним из наиболее распространенных методов аппроксимации для интегрирования нелинейных дифференциальных уравнений вынужденных колебаний.
Если вы хотите определить только первое приближенное значение jcx alsin rf, то вам нужно составить дифференциальное уравнение 2-го приближенного значения и приравнять коэффициент stnpt к нулю см. Раздел 7, затем вычислить амплитуду av. Тогда 2-е приближение не вычисляется с большими усилиями см. 8 и 9. Заметим, что если перейти от 2-го приближения к 3-му особенно ко всем последующим, то объем вычислений резко возрастет, а точность результата увеличится незначительно. Поэтому она обычно ограничивается определением 2-го приближения.
Задача 20.8. Найти периодический закон вынужденных колебаний точки масс m, которая движется вдоль оси x под действием нелинейной упругой силы F и возмущающей силы S с жесткими свойствами. Проекция этих сил на ось x равна Hx — ctx-ctx , SX H sin pt. Где ct ct и H-положительные постоянные коэффициенты, а c и H-малые параметры. Эта задача решается методом последовательных дуффинговых приближений, который описан в обзоре теории. Найдите первое и второе приближения. Решение. Дифференциальное уравнение массовой точки mX Fx Sx после подстановки значений Fx и 5X принимает вид mx — ctx-cp Wsinpf, то есть Джей — к Х-Х — УГ ДНР, 1 Где k Ди м, ф квю, ч — ч м.
Заметим, что, как и c и H, коэффициенты y и ft являются малыми параметрами, y 0 и u 0. При определении первого приближения xx будем считать, что y 0 в уравнении 1.Линейные дифференциальные уравнения — k x — hs. легко видеть, что npt удовлетворяет решению. ХХ axslnpf, 2 Где ah-константа, которая будет определена позже. Используйте уравнение 1 в качестве первого приближения к нелинейному дифференциальному уравнению 2. Перейти ко 2-му приближению definition.
- To для этого добавьте термины слева и справа от выражения 1 Х х п -Аи х-1 х ftsinpf. Расчет 2-го приближения сводится к интегрированию дифференциальных уравнений 3.Справа от него 1-е приближение 2 заменяется на x. Х р х АИ п -А2 грех пт — СЛН ПФ ФТ греха пт для СЛН ПРОМАЛЬП 3 греха пт-грех 3 ПТ, представьте себе это Уравнение формы л р х Асин РФ г yafsin 3 ПТ, 4 Где это показано Поскольку термин AsinpA включен в правую часть, легко видеть, что случай резонанса соответствует дифференциальному уравнению 4.фактически, 1 из этого частного решения является x — icos rt, бесконечно увеличивающимся с течением времени. Условия определяют периодический закон движения points.
В правой части Формулы 4 термина Asin rf не существует, то есть коэффициент A должен быть равен нулю. Используя формулу 5, Р −4, −4×4 −0. Уравнение 6 позволяет определить величину амплитуды амплитуды амплитуды а в первом приближении в зависимости от круговой частоты Р возмущающей силы. Графический метод решения этого уравнения показан ниже. При выполнении условия 6 дифференциальное уравнение 4 принимает вид р х йадж греха 3 л 7 Общим решением xi уравнения 2, которое является желательным 2-м приближением, является формула J X2 X2, 8 Где xi1 — решение соответствующего однородного уравнения, а x — конкретное решение уравнения 7.
На боковой поверхности кругового конуса симметрично расположены два груза, соединенные между собой тонкой нитью и отстоящие от оси вращения конуса па расстоянии одной трети радиуса основания конуса. Людмила Фирмаль
Это легко увидеть. x i bxsinpt Является 1 из решения однородного уравнения X p x 0.Параметр bx определен ниже. Следуйте правой части выражения 7, чтобы найти конкретное решение x G в виде ХВ Дсин 3 ПТ. 10 Подставляя функцию 10 и ее вторую производную Xi — 9Dp2sin3pZ в уравнение 7, находим D -уа 32р2 и вводим значение этого D в конкретное решение 10. 8 из 9 и II получить 2-е приближение, используя результат. x, b1sinp — fSin3pt 12 После дуффинга, мы сделаем коэффициентов AX и BX равны.
Они находятся в sinptf в первом 2 и втором 12 приближениях. Тогда мы, наконец, получаем 2-е приближение искомого периодического движения. ХГ грех пт-грех 3 пт 13 Если мы сравним 1-е 2 и 2-е 13 приближения, то увидим, что их разность xt-Xi имеет порядковую величину малость параметра y. — 3 ПТ СЛН. В заключение рассмотрим графическое решение уравнения 6 для определения зависимости возмущающей силы амплитуды а первого приближения от круговой частоты р. Отметим формулу 6. Таким образом, определенный диапазон значений p соответствует 3 значениям ax. Левая и правая части уравнения 14 представлены y 15.
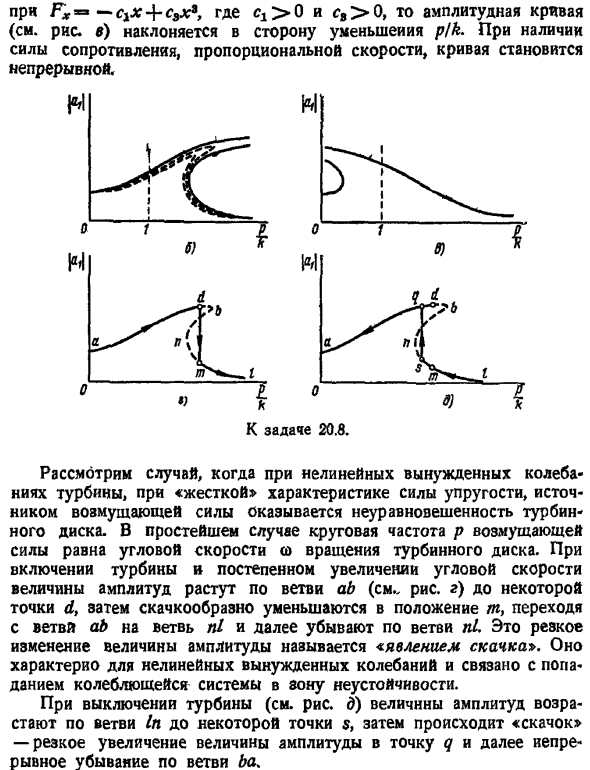
Рисунок отображаются Декартовые оси, значения ab отображаются на горизонтальной оси, а значения y отображаются на вертикальной оси. Функция y pat соответствует независимой параболе 3-го порядка. В какой-то момент см. рисунок а. И затем… значение p k. Функция j jp-4-l Oi соответствует пучку линий, проходящих через точку. Линия, равная −1, зависит от соотношения круговой частоты p k возмущающей силы и свободного колебания.
Так, величина p A 0 соответствует прямой линии a-a, угловой коэффициент соответствует минус 1, величина p k 1 соответствует прямой линии 0-0, а угловой коэффициент соответствует 0.Значение Л оо-прямая линия, совмещенная с осью Y, угловой коэффициент равен infinity. So, если p k непрерывно изменяется от нуля до бесконечности, прямая a — a вращается против часовой стрелки до тех пор, пока не совпадет с осью Y. если p k O, то линия a-a пересекает параболу с определенным значением p k, линия Нажмите одну ветвь параболы и перейдем на другую ветку. если p k еще больше увеличить, а затем повернуть линию, то линия пересечет параболу в 3 точках.
Абсцисса пересечения прямой и параболы фиксирует искомое значение dp. В дальнейшем это называется амплитудой нелинейных вынужденных колебаний. Это название условно, но вполне оправдано тем, что в Формуле 13 оно является a, yaf 32 fact. Рисунок Б построение кривой f p k. как видно, не 1 амплитуда av, а 3 соответствует определенному диапазону p k Values. In сравнение с соответствующим графиком линейной упругой силы см. Рис. 2 на стр. 111 в томе 8.14, амплитудная кривая стр. 373 см. кривую — на рис. 20.1, остается прерывистой и наклоняется в сторону увеличения p k отметка абсциссы на рис. b соответствует резонансу, вызванному линейной упругой силой.
Если решить соответствующую задачу с учетом сопротивления, пропорционального скорости, то кривая будет непрерывной см. пунктирную кривую на рисунке Ff. в этом случае при увеличении сопротивления площадь 3 амплитуд уменьшается. Аналогичный шаг будет обсужден позже в выпуске 20.9. Если решить эту задачу в случае мягких свойств силы упругости см. рис. 373 на стр. 20.1, кривые 2-2, то есть, если — c x CiX , где Ci 0 и cs 0, амплитудная кривая см. Рисунок c наклоняется в сторону уменьшения p k.
Если существует сопротивление, пропорциональное скорости, кривая Рассмотрим случай, когда диск турбины несбалансирован из-за жесткости, характерной для упругой силы, которая является источником возмущающей силы, при нелинейном вынужденном колебании turbine. In в простейшем случае круговая частота P возмущающей силы равна угловой скорости вращения W диска турбины. При включении турбины и постепенном увеличении угловой скорости амплитуда увеличивается вдоль ветви ab см. Рисунок D до некоторой точки d, затем резко уменьшается до положения m, затем переходит от ветви ab к ветви nl и уменьшается вдоль ветви l .Внезапное изменение величины этой амплитуды называется феноменом скачка.
Это характерно для нелинейных вынужденных колебаний, которые связаны с колебательными системами, попадающими в неустойчивую систему. Когда турбина выключена см. Рисунок е, амплитуда увеличивается вдоль ветви in до определенной точки s и происходит скачок.
Смотрите также:
Предмет теоретическая механика
