Многократное измерение

Многократное измерение

• Проводятся множественные измерения одного и того же постоянного размера, что повышает требования к точности измерений. Такие измерения характерны для профессиональной метрологической деятельности и проводятся в основном сотрудниками государственных и ведомственных метрологических служб, а также тонкими научными экспериментами. Это сложные, трудоемкие и дорогостоящие измерения, и их обоснованность всегда должна быть убедительной. Л. Бриллюэн, один из основателей теории информации, написал.

В своей статье Теория информации и ее применение к основным проблемам физики . Процитировал фразу Габора Я не могу ничего дать, включая информацию . Это относится исключительно к информации об измерениях. Количественный анализ нескольких измерений показывает, что его главной особенностью является прием и использование большого количества информации об измерениях в обратном направлении. Это не значит, что вам не нужно анализировать априорную информацию. Такой анализ обязательно предшествует множественным измерениям и имеет те же цели, что и одно измерение, с той разницей, что множественные измерения устанавливают экспериментальные распределения вероятностей результатов измерений.

Соседний цилиндр представляет собой цилиндр с наименьшим диаметром, описанным вокруг фактической внешней поверхности, а наибольший диаметр цилиндра вписан в фактическую внутреннюю поверхность. Людмила Фирмаль

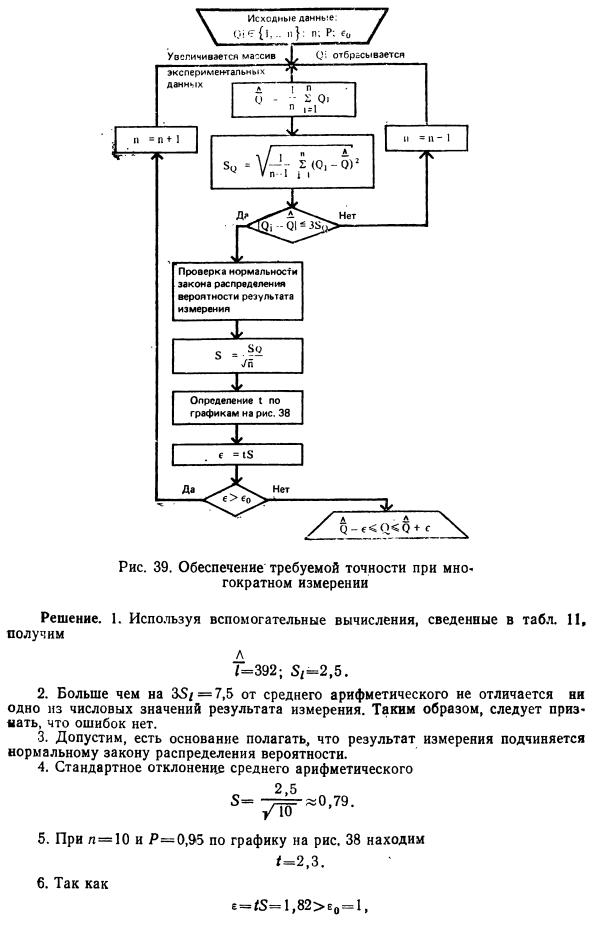
Процедура выполнения нескольких измерений показана на рисунке. 32 (см. Вставку в конце книги). После анализа предварительной информации и тщательной подготовки к измерению принимаются n независимых показаний. Эта основная процедура измерения может быть организована различными способами. Если вы можете игнорировать изменение измеренных значений с течением времени, проще всего получить все значения задания, которые являются случайными числами, повторив операцию сравнения (2) с использованием того же инструмента измерения.

Исходя из априорной информации, если вы можете сделать вывод, что измерение существенно изменяется во время такой процедуры, каждый из них измеряется одновременно несколькими приборами, давая одно из независимых показаний , Все значения ссылки x передаются в чтение X с поправкой на 0, независимо от того, как оно получено. Когда несколько измерений выполняются на одном приборе, поправки могут отличаться друг от друга из-за изменений фактора влияния во времени. Когда использовать При одновременном использовании нескольких инструментов компенсация зависит от индивидуальных характеристик.

Для простоты они однозначно известны. Весь массив экспериментальных данных = X + 0r; E (1, …, A Характеризует результаты измерения O- также можно описать с помощью функции распределения вероятности O. Однако необходимо проверить, есть ли какие-либо ошибки в получении отдельных значений результатов измерений. Причины ошибок и 3 правила сигма , используемые для их выявления, описаны в разделе. 3.3. Чтобы использовать это правило, вам необходимо знать числовые свойства закона распределения вероятностей результатов измерения, то есть среднее 2 и среднеквадратичное отклонение od. Однако, как уже упоминалось в разделе.

В 3.1 и 3.4 их невозможно вычислить из-за практической невозможности интегрирования в конечных n и бесконечных пределах. Можно только каким-то образом оценить свойства эпи-числовых значений на основе ограниченных экспериментальных данных и показать их аппроксимации или пределы, в которых они находятся с определенной вероятностью. Оценка числовых характеристик закона распределения случайной или количественной вероятности представляется точкой на оси значений и называется точкой, интервалом-интервалом. Доверительный интервал является примером последнего.

В отличие от самих числовых свойств, оценка является случайной, а значение зависит от количества экспериментальных данных, а закон распределения вероятностей зависит от закона распределения вероятностей или значения меры самого случайного числа. Оценка должна соответствовать трем требованиям. Состоятельный, справедливый и эффективный. Действительным является оценка, которая с вероятностью сходится к оценочному числовому свойству.

Несмещенный — это оценка, математическое ожидание которой равно расчетной числовой характеристике. Действительным является одна из нескольких возможных несмещенных оценок с минимальной дисперсией. Рассмотрим n независимых значений, полученных путем измерения физической величины постоянного размера. Как и раньше (см. Раздел 3.4), предположим, что каждое из них отличается от среднего на b . Ох = О4-8, 2, = 04-8 ;; 0.5-04-8,; O = O4-8 , Где случайная величина b следует центральному закону симметрии распределения вероятностей. Сложите левую и правую части этих уравнений вместе и разделите на n. d + A Добавить А.

Вероятность сходится к C и может быть использована в качестве согласованной точечной оценки с использованием закона симметрии распределения вероятностей результатов измерений. Среднее значение. Это называется среднее арифметическое.

Математическое ожидание среднего арифметического м (А2о ) а5 больше ) АД М (5) + М ( ,) = , Следовательно, среднее арифметическое является не только последовательным, но и объективной оценкой среднего значения результатов измерений. Это также эффективная оценка, потому что дисперсия всех других несмещенных оценок минимальна. Независимо от закона распределения вероятностей, среднее арифметическое отклонение: o (4A .

В качестве точечной оценки: По аналогии со средним арифметическим, дисперсия результатов измерений выглядит следующим образом: A — > —A- 2 , -§ + b-5) -A.D (c, — > — ( — -Эй, -о + (5-5 г- В случае симметричного закона распределения вероятностей результатов измерений, если -> ° °, второй член в правой части имеет тенденцию быть нулевым, поэтому эта оценка непротиворечива, поскольку первый член приближается к t. вы. но ТАМ в — ^ = Другими словами, такие оценки являются предвзятыми. Несмещенную оценку можно получить, умножив ее на коэффициент n — 1.

Для n-> oo этот коэффициент имеет тенденцию равняться 1, поэтому несмещенная оценка дисперсии результатов измерения равна Мы остаемся богатыми. Ее квадратный корень 5 = при 2 А, -5> Это называется стандартным отклонением. После оценки среднего значения O и стандартного отклонения Od результатов измерений вместо этих числовых характеристик используйте правило 3 сигм для оценки точечной оценки и использовать подозрительное значение 2 неправильно. Если они отличаются от среднего арифметического 2 и 35 секунд, их следует отбросить. Окончательное значение затем рассчитывается. и Пример 22.

Пятнадцать независимых чисел измерений комнатной температуры по шкале Цельсия приведены во втором столбце таблицы. 6. Таблица 6 А ,, — м (-0 * 1 1 из 4 5 1 2 3 5 6 7 8 20,42 43 40 43 42 43 39 30 +0,016 + 0,026 -0,004 +0,026 +0,016 +0,026 -0,014 -0,104 0,000256 676016 676 256 676196 10816 +0,009 + 0,019 -0,011 + 0,019 + 0,009 + 0,019 -0,021 0,000081 361 121 361 081 361 441- продолжение 2 , = 20,404. 2. При определении стандартного отклонения результаты вспомогательных расчетов обобщаются в четвертом столбце таблицы. 6 * определение 5. Результат вспомогательного расчета стандартного отклонения уменьшается до пятого и шестого. 5 = 0,016. 6.

Ни одно из оставшихся значений / не отличается от среднего арифметического более чем на 3 5 = 0,048. Поэтому можно предположить, что никто из них не прав. При оценке числовых свойств закона распределения вероятностей результатов измерений предполагается, что результаты измерений следуют нормальному закону распределения вероятностей для всей дальнейшей обработки экспериментальных данных, за исключением ошибок. Вы также должны проверить правильность этого предположения. Независимо от того, допустимо ли предположение о том, что результаты измерений соответствуют нормальному закону распределения вероятностей, его уже можно оценить по типу гистограммы, построенной на экспериментальных данных.

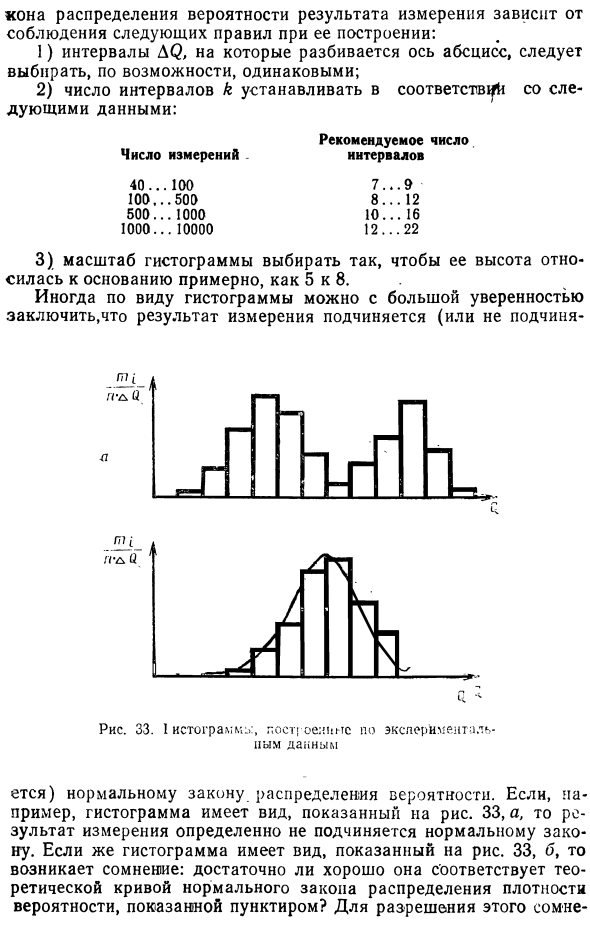
Порядок его построения обсуждается в примере 11. Рекомендуется использовать при выполнении таких расчетов Конус распределения вероятности результатов измерения зависит от соблюдения следующих правил при его построении: 1) Если возможно, выберите тот же интервал для деления горизонтальной оси. 2) Количество интервалов для установки в соответствии со следующими данными: Количество измерений Рекомендуемый номер интервал , , , 11H1 100 .. .500 500 … 1000 1000 ..

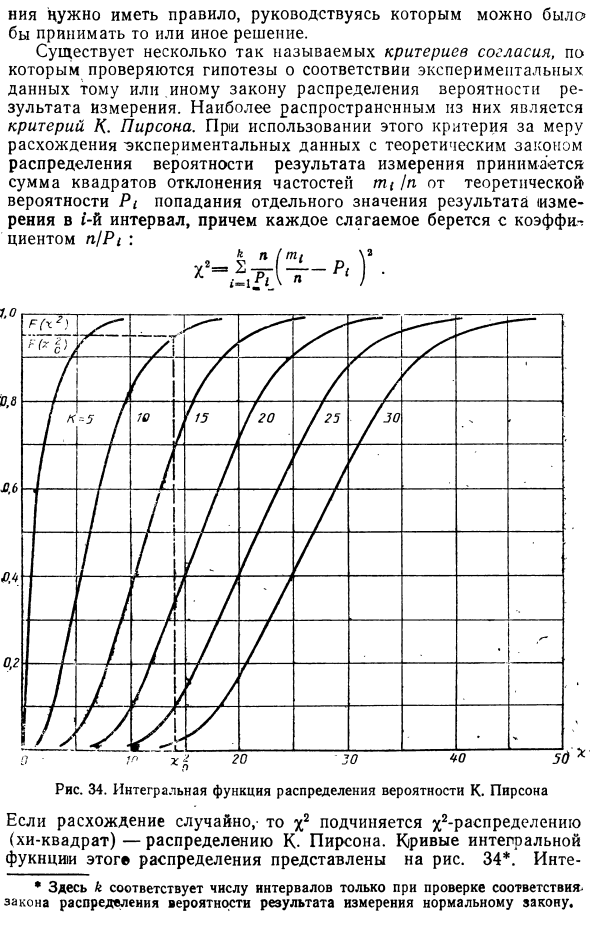
Выберите шкалу гистограммы, чтобы обратиться к базе с высотой около 5-8. Иногда внешний вид гистограммы позволяет уверенно сделать вывод, что результат измерения является зависимым (или не зависимым). есть) Нормальный закон распределения вероятностей. Например, если формат гистограммы 33a на рисунке 5, результаты измерений явно не подчиняются обычным законам.

Если гистограмма имеет вид, показанный на рисунке 33b, то возникает вопрос: хорошо ли она соответствует теоретической кривой закона распределения плотности вероятности, обозначенной пунктирной линией Чтобы решить этот вопрос Вам нужно иметь правила, которые позволят вам принять то или иное решение. Существует несколько так называемых критериев согласия, которые проверяют гипотезу о том, соответствуют ли экспериментальные данные тому или иному закону распределения вероятностей результатов измерений. Наиболее распространенным из них является К. Стандарт Пирсона.

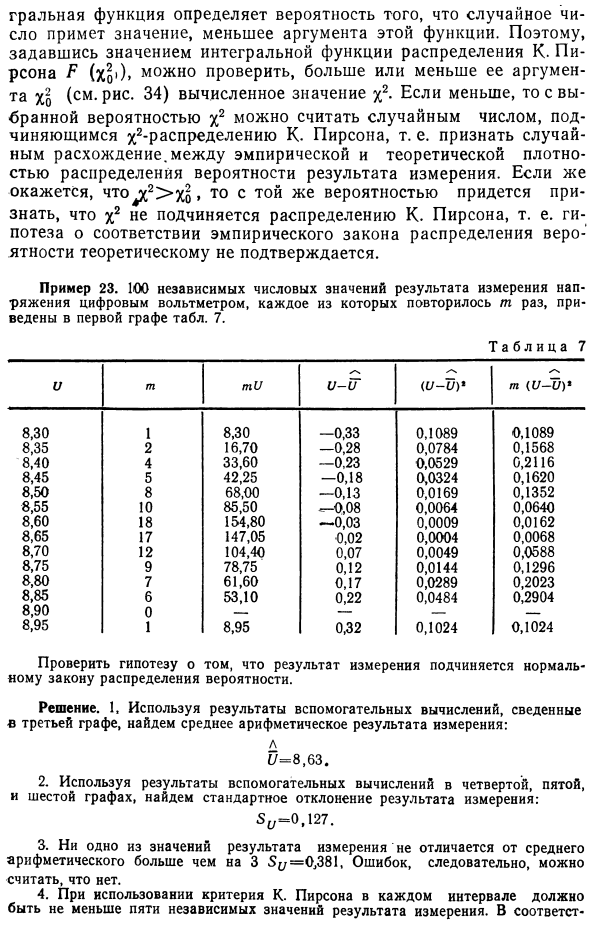
При использовании этого критерия сумма квадратов отклонений частоты / n от теоретической вероятности P /, попадающих в отдельные значения результата (измеряется на / -ом интервале, каждый член представляет собой коэффициент n / P : Если несоответствие является случайным, x2 следует распределению x2 (хи-квадрат) — распределению K Пирсона. Кривая интегральной функции этого распределения показана на рисунке. 34 *. между Здесь k соответствует количеству интервалов только при проверке правила соответствия регулярному правилу распределения вероятностей результата измерения. Линейная функция определяет вероятность того, что случайное число будет меньше аргумента этой функции.

Поэтому, учитывая значение интегральной функции распределения K, мы можем проверить, является ли Пирсон P (X0 ) , аргумент% 2 3 4 больше или меньше своего аргумента% 5 (см. Рисунок 34). Рассмотрим случайные числа, которые следуют за распределением К. Пирсона x2. Другими словами, разница между эмпирической плотностью и теоретической плотностью распределения вероятностей результатов измерений признается случайной. Если окажется, что 4×2> X0, это следует признать с той же вероятностью, что x2 не следует распределению К. Пирсона. Пример 23.

Используйте результаты вспомогательных расчетов в 4-м, 5-м и 6-м столбцах, чтобы найти стандартное отклонение результатов измерений. 5 лет = 0,127. 3. Поскольку значение результата измерения не отличается от среднего арифметического более чем на 3 8i = 0,381, можно предположить, что ошибки нет. 4. При использовании критериев К. Пирсона каждый интервал должен иметь не менее пяти независимых значений результатов измерений. И поэтому Она была представлена (Т -1 руб. * C, -Г и1> лр.

• Определите границы Сколько 6. Определить с вероятностью по значению В частности, отдельные значения результатов измерений, которые следуют нормальному закону распределения вероятностей, классифицируются на вероятные интервалы. Если он вдвое меньше, он попадает в левую или правую половину этого интервала. Это вероятность. 3.3 определяется вероятностной интегральной функцией Лапласа E- (//), поэтому вы можете использовать таблицу функций Лапласа вместо графика для повышения точности вычислений. Значение b (O), полученное из таблицы, указано в пятом столбце таблицы. 8. 7.

Согласно нормальному закону распределения вероятностей, теоретическая вероятность того, что P / попадает в первый интервал единственного значения результата измерения, явно Учитывая, что b (-oo) равно -0,5, а b (oo) = 0,5, поместите рассчитанное значение в шестой столбец таблицы. 8. 8. Седьмой и восьмой столбцы содержат результаты остальных вспомогательных расчетов. Х = 2,528. 9. Из графика на фиг.34 видно, что вычисленное значение X2 Xo соответствует, например, вероятности 0,95.

Эти методы не только обеспечивают точность процесса среди заданного технического сопротивления при низких затратах, но и позволяют создавать пределы технической точности. Людмила Фирмаль

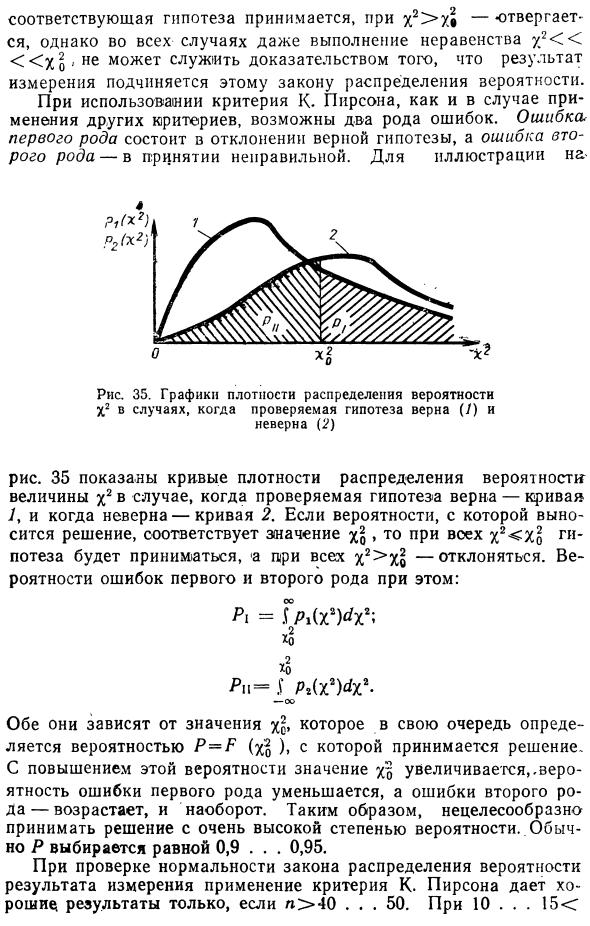
Поэтому мы можем принять гипотезу о том, что результаты измерений следуют нормальным законам. Критерий соответствия К Пирсона широко используется для проверки гипотезы о том, что результаты измерений следуют четко определенному закону распределения вероятностей. Когда х2 х0 Если x2> y, соответствующая гипотеза принимается, но во всех случаях даже реализация неравенства y, 2 Xo не служит доказательством того, что результаты измерения подчиняются этому закону распределения вероятностей , При использовании критериев К. Пирсона, могут возникнуть два типа ошибок, как и с другими критериями. Первый тип ошибки — отклонение правильной гипотезы, а второй тип ошибки — принятие неверной гипотезы.

Плотность распределения вероятностей проверенной гипотезы верна (/) и ложна (2) На рисунке 35 показана кривая плотности вероятности для x2, когда проверочная гипотеза верна (кривая 1 неверна). 2. Если вероятность принятия решения соответствует слабости x§>, если война X2 Ho gi, протез будет принят, и все x2> Xb будут отклонены. Вероятность ошибок типа 1 и 2 в этом случае: A = Ga (x ) ^ x2; / N = ^. (X Mx * — Оба зависят от значения х2. Это значение зависит от вероятности принятия решения P = P (xo). Если эта вероятность увеличивается, х Вероятность ошибок типа 1 уменьшается, ошибки типа 2 возрастают, и наоборот.

Поэтому нецелесообразно принимать решения с очень высокой вероятностью. Обычно P выбирается равным 0,9 … 0,95. При проверке нормальности закона распределения вероятностей результатов измерений применение критерия Пирсона дает хорошие результаты только при n> 40 … 50. , , 15 D n 40 … 50 Так называемые составные критерии принимаются. Первый рассчитан -X ~ Я Состояние проверено Где ^ W P и go зависят от вероятности P, что решение будет принято и находятся в таблице9.

Таблица 9. Далее, если условие выполнено. Проверен хвост теоретических и эмпирических законов распределения вероятностей. Для 10 n ^ 20, если 20 n 50-2, считается приемлемым отклонение одного из измеренных значений от среднего арифметического более чем на 2,5 5d.

Если хотя бы одно из этих условий не выполняется, достаточно отвергнуть гипотезу нормальности закона распределения вероятностей результатов измерений. В противном случае гипотезой является вероятность P ^ P1 + ** — Принято Если n 10 … 15, гипотеза о том, что результаты измерений следуют нормальному закону распределения вероятностей, не подтверждается. Решение основано на анализе трехэтапной информации. Основная идея множественных измерений одной и той же переменной постоянного размера состоит в том, чтобы перейти от результата измерения 0 к его среднему арифметическому .

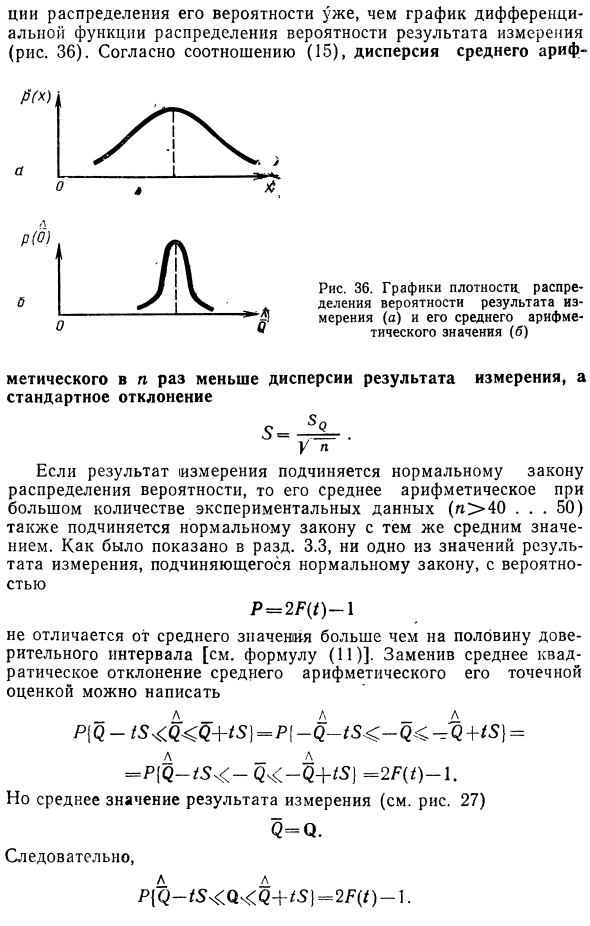
Среднее арифметическое представляет собой случайное значение измеренной величины, аналогичное результату измерения, График дифференциальной функции Распределение распределения вероятностей является более узким, чем график дифференциальной функции распределения вероятностей результатов измерений (рисунок 36). Согласно соотношению (15), дисперсия среднего арифметического Стандартное отклонение График плотности вероятности распределения результата (а) и его среднего арифметического (б) Измеренное значение 5. Если результаты измерений следуют нормальному закону распределения вероятностей, среднее арифметическое большого количества экспериментальных данных.

Следует нормальному закону того же среднего значения. Как указано в разделе. 3.3, все измеренные значения следуют нормальному закону и являются вероятностями P = 2P (() -1 Он не изменяется от среднего значения за половину доверительного интервала Справочная формула (11) . Замена стандартного отклонения среднего арифметического с этой точечной оценкой, = P (y- / 5h -yo -5 + / 5) = 2P ( ) — 1. Однако среднее значение результатов измерений (см. Рисунок 27) так P — / x bx g + / = 2 (/) — 1. (Возвращаясь к обсуждению на рисунке 28, полезно представить график распределения плотности вероятности среднего арифметического). Соответствующий порядок расчета показан на рисунке. 32.

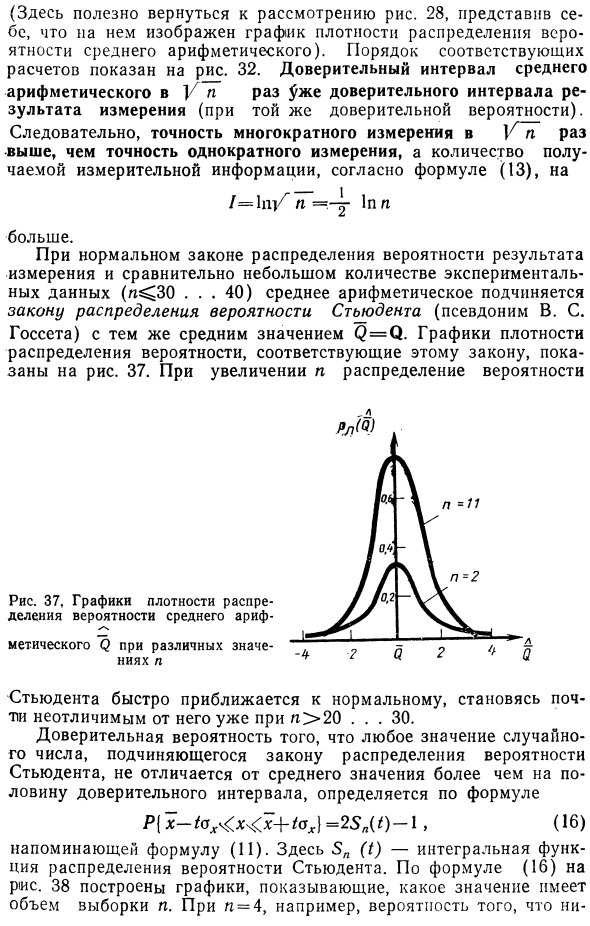
Доверительный интервал для n арифметических средних Тот же доверительный интервал для результатов измерений (та же самая доверительная вероятность). В результате точность нескольких измерений в ~ n раз выше, чем точность одного измерения, и в соответствии с уравнением (13) количество полученной информации об измерениях составляет / = 1n / n = .- ^ 1pp Даже больше. В нормальном законе распределения вероятностей результатов измерений и относительно небольшом количестве экспериментальных данных (n ^ 3 … 40) среднее арифметическое соответствует закону распределения вероятностей Стьюдента (псевдоним V. S. Gosset) с тем же средним значением = 0.

График плотности распределения вероятностей, соответствующий этому закону, показан на рисунке. 37. При увеличении n распределение вероятностей Рисунок 37. График плотности p, делящий различные средние метрические вероятности 2. Вскоре ученики приближаются к нормальному состоянию и уже почти не различимы при n> 20 … 30.

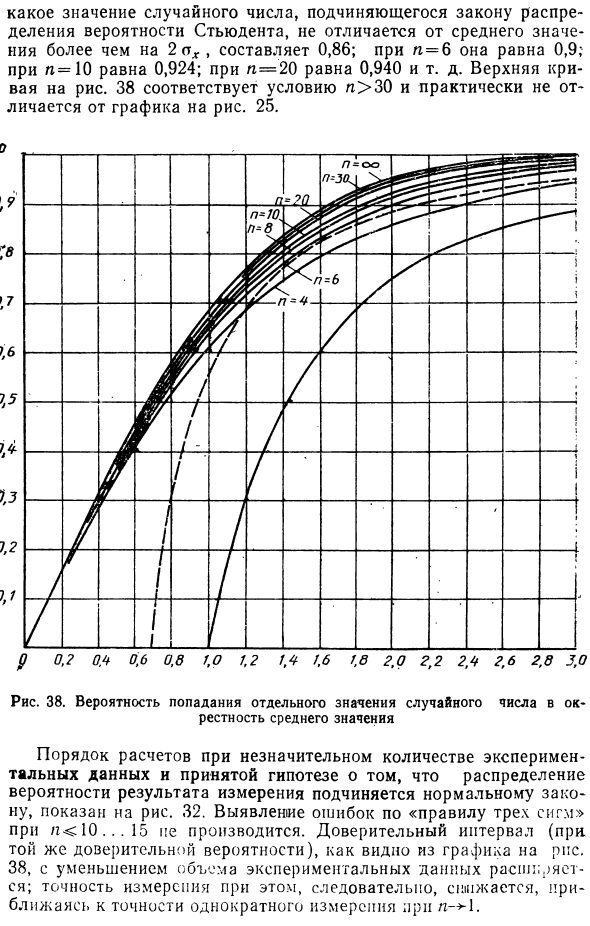
Формула определяет доверительную вероятность того, что случайное значение, которое подчиняется закону распределения вероятности Стьюдента, не отличается более чем на половину среднего значения и доверительного интервала. P = 25 (0-1 (16) Аналогично уравнению (11). Здесь 5 (I) -интегральная функция распределена по вероятности Стьюдента. Уравнение (16) на диаграмме дает 38 графиков, показывающих важность размера выборки для n.

Например, если n = 4 Значение случайного числа по закону распределения вероятностей студента составляет 0,86, что не отличается от среднего значения за 2 mx. Для n = 6 это 0,9. Если n = 10 равно 0,924, если n = 20, оно равно 0,940 и т. Д. 38 соответствует условию n> 30 и фактически совпадает с графиком на фиг. 38. 25. На рисунке показана процедура расчета с использованием небольшого количества экспериментальных данных и общая гипотеза о том, что распределение вероятностей результатов измерений следует нормальному закону. 32. Если n 10 … 15, ошибка не обнаруживается в соответствии с правилом 3 сигм .

Как видно из графика на чертеже, доверительный интервал (с той же вероятностью вероятности) 38 увеличивается с уменьшением количества экспериментальных данных. Следовательно, точность измерения в этом случае снижается и приближается к точности одного измерения, когда i-> 1. Если гипотеза о нормальности результата измерения отклоняется, в зависимости от типа гистограммы, вы можете по крайней мере выдвинуть гипотезу симметрии или асимметрии в законе распределения вероятностей результата измерения.

Если гистограмма симметрична с использованием тех же критериев, проверяется соответствие между законом распределения вероятностей результатов измерений и одной из стандартных функций приближения, показанных в таблице 1. 10. Выбор функции стандартной аппроксимации основан на априорной информации. Например, при измерении частоты с помощью цифрового измерителя частоты на основе количества импульсов заранее известно, что результаты измерения соответствуют тригонометрическому закону распределения вероятностей. Поэтому естественно выбрать эту функцию в качестве стандартного приближения, если можно игнорировать другие влияющие факторы.

В соответствии с критериями соответствия, экспериментальные данные проверяются на природу следующей гипотезы: Результаты измерений зависят от того, соблюдается ли этот закон распределения вероятностей. Результат повторного тестирования не служит доказательством, а лишь устанавливает степень обоснованности гипотезы. Во многих случаях эмпирическое распределение вероятностей хорошо аппроксимируется различными функциями. Это говорит о том, что есть несколько решений проблемы. Характерной чертой стандартных аппроксимационных функций является то, что они усекаются. Такая функция теряет значение доверительного интервала, соответствующего конкретной доверительной вероятности.

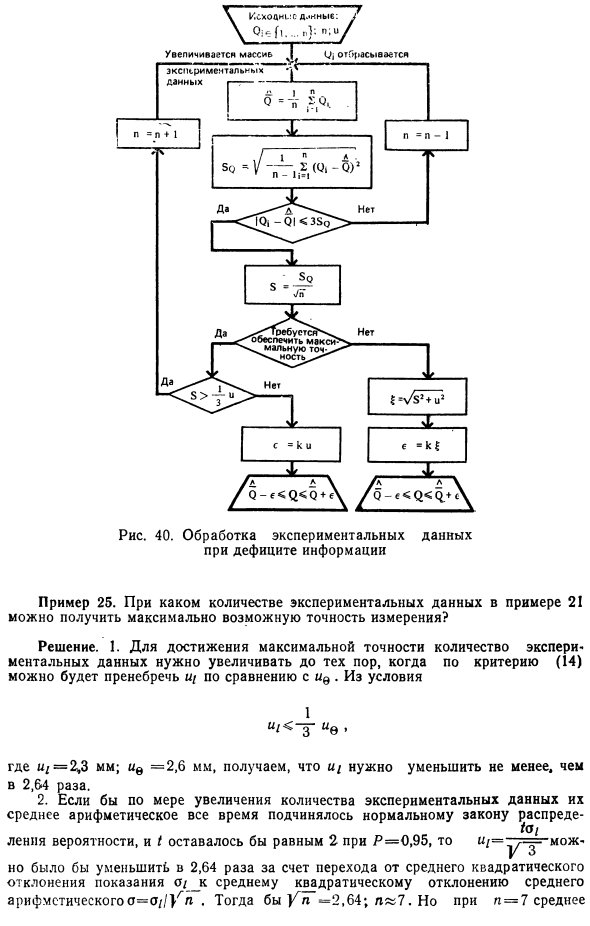
Вместо этого согласно MI.1317-86 GSI. Характеристики результатов измерений и погрешности измерений. Форма представления. Как использовать при тестировании образцов продукции и мониторинга параметров. Используется аналог с доверительным интервалом с полушириной, равной aa. Где а является аналогом коэффициента I. Вместо 10 и его стандартного отклонения, его оценка используется как обычно. Соответствующий порядок расчета показан на рисунке. 32. В зависимости от типа гистограммы закон распределения вероятностей результатов измерений нельзя считать симметричным или если ни одна из функций аппроксимации не подходит, особенно для точных и важных измерений.

Возникает проблема определения действительного закона распределения вероятностей результатов измерений. Четкого решения нет, и вывод о том, что экспериментально найденная плотность распределения вероятностей следует определенному закону, может быть сделан только с той или иной вероятностью. Правила проверки соответствия экспериментального и теоретического распределений регламентируются ГОСТ 11.006 74. Основные требования к проведению исследований, порядок математической обработки эмпирических данных и выбора математических моделей распределения устанавливаются специальными документами Госстандарта М.И. 199-79.

Это довольно сложная и длительная процедура, требующая значительных дополнительных затрат. И необходимость в отдельных случаях должна быть обоснована технически и экономически. Во многих случаях, когда точность жертвуется, устанавливается предел, который не может превышать значение измеряемой величины в соответствии с законом распределения вероятностей результата измерения. Например, если гистограмма асимметричная, среднее арифметическое представляет собой последовательное отклонение от среднего. Нет оснований полагать, что последнее равно измеренному значению.

В этом случае среднее арифметическое просто считается новой переменной, и ее дисперсия в несколько раз меньше дисперсии результатов измерения в соотношении (15). В этом случае оценка отклонения и стандартное отклонение ранее использованных результатов измерений также будут нарушены. Следовательно, оценка дисперсии результата измерения определяется с использованием свойства четвертой дисперсии, заменяя отображаемое там математическое ожидание средним арифметическим.

Смотрите также:

Предмет метрология

Измерительная информация	Обработка результатов нескольких серий измерений
Однократное измерение	Воспроизведение единиц физических величин