Оглавление:


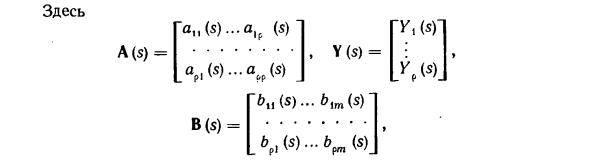







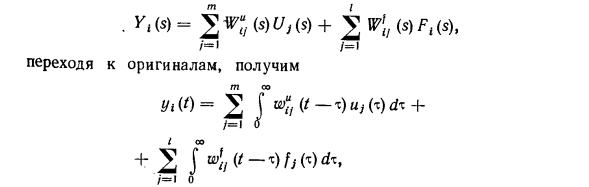



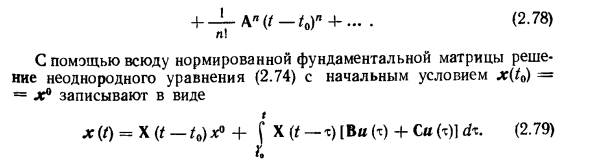

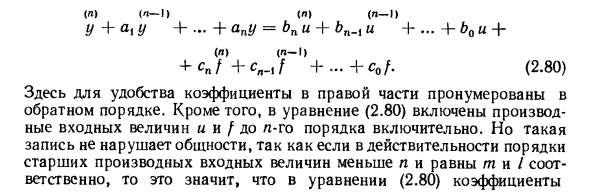


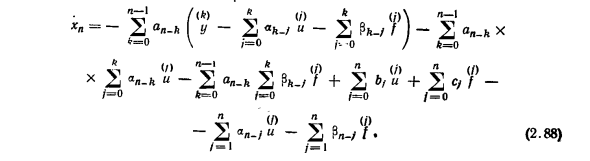



Многомерные стационарные линейные системы
- Многомерная стационарная линейная система Многомерные системы или несколько подключенных систем управления называются системами автоматического управления, и существует множество (несколько) контролируемых величин. Таким образом, объект с некоторой контролируемой величиной называется многомерным объектом или многосвязным объектом управления. Примеры многомерных объектов, являются следующими :. Самолет, чьи контролируемые величины: нос, углы наклона и крена, высота и скорость. Паровой котел, температура, давление пара и другие величины которого регулируются.
Поэтому многомерные системы также определяются как автоматизированные системы с многомерными (векторными) выходами. Многомерные системы и объекты называются линейными и стационарными, когда они описываются системой линейных дифференциальных уравнений с постоянными коэффициентами. Многомерные стационарные линейные системы и уравнения объектов. Предположим, что yi9 и y9 являются выходными величинами, u и n являются параметрами управления или движущими действиями, а f ,, …, // оказывают возмущающее влияние.
Обычно контрольная сумма называется выходной или выходной суммой. Людмила Фирмаль
В общем случае многомерная стационарная линейная система и уравнения объектов могут быть записаны в виде следующей системы: DM {Р) Y1 + ••• + AIP (Р) * / р = & П (Р) «IH —- + ХТ {Р) УМ + (/>) / «+ ••• + s и (p) /„ Да, fj = b (/), а все остальные мешающие эффекты и параметры управления равны нулю. Подобно матрице переноса, матрица весов обеспечивает полное описание многомерной системы (объекта). Установите связь между матрицей веса и матрицей переноса. Согласно определению (2.63) передаточная функция W (s) Y {(s) = W ^ (s) U, (s) t 1 = 1, …, p. (2,70) (Jj (s) = L ($ (/)) = 1 и yt (t) = wutj (t) для wy = S (/) и других входных действий равны нулю, поэтому из уравнения (2.70) 00 p; / = I, …, m. Можно показать это также <(S) = (/)} = J (t) e to st dt, i = 1, …, p, / = 1, …, /. (2,72)
Следовательно, передаточная функция (элементы матрицы переноса) равна изображению Лапласа весовой функции (элементы матрицы веса). Матричные форматы (2.71) и (2.72) имеют следующий формат: 00 Wu (s) = L {w ° (0} = w ° (/) erst dt, о и w / (s) = L {w ‘(/)> = I w / (/) e_s / dt По определению интеграл матрицы равен матрице интегралов ее элементов. Напишите выражение для определения выходного значения по весовой матрице любого входного воздействия. Если элемент передаточной функции является весовой функцией и используется теорема о свертке, (2.68) , Yt (s) = 2 K «Yy M + 2 K (s) Pt (s), / = i / = i передается оригиналу, Т.С. И м-2 I + / -1 O 2 + F »{/ <-? > // (> *. О / = 1 Эта система в матричном формате 00 00 г (/) = у ш * (* — • с) е (Т) дх + J, ш «(е-х) / (т) дт. 0 0
- Поэтому «Соотношение между выходной величиной и входной величиной с использованием весовой матрицы описывается так же, как и в одномерном случае. Написать дифференциальное уравнение в нормальной форме Коши. При рассмотрении многих задач полезно иметь уравнения для одномерных и многомерных систем, записанные в виде обычных систем. Нормальная система или система нормальной формы Kshi — это система дифференциальных уравнений первого порядка, решаемых в терминах производных. В частности, нормальная система линейных дифференциальных уравнений называется системой T * i = 2 a ‘x’ + 2bit и ‘+ 2Cu 1 = lf I / = 1 В матричной форме x = \ x + Bx + C /. где р. (2,73) (2,74) » 0 | ‘1 и * И- * -ap \ -Kp J. Это. «L j _ * n J B «■ bn … bx » l» »cJ -‘i ‘ Louis-PT это. L см-CNL. A = X = х =
Вектор называется фазовым вектором или вектором состояния, а его координаты xi xn являются фазовыми координатами. Этот вектор называется управляющим вектором или просто контролем, его координаты uit …, параметры управления um. Называется ли вектор / вектором возмущения k — это просто возмущение, а его /-я координата называется / -ым возмущением или / -ым возмущением. Рассмотрим однородные уравнения наряду с неоднородными уравнениями (2.74) х = \ х (2,75) π (= = (.x \ «…., x <«) T, * <2) = (*; 2>, …, X ™ Y …… * <«> = = (Xjrt), …, x1n) y образует n линейно независимых решений этого Уравнение.
Матрицы столбцов x и и / также называются векторами. Людмила Фирмаль
Такая система называется базовой системой для решения уравнения (2.75). Построить матрицу, исходя из t-го решения из базовой системы в качестве i-го столбца. г <1> лп) л …. л F (0 = н н Эта матрица называется фундаментальной матрицей уравнений (2.73), (2.74) и (2.75). Когда t = f, если фундаментальная матрица является единичной матрицей E (Φ (/ 0) = E), соответствующее фундаментальное решение называется нормализацией. Φ (Если 0 — нормализованная базовая матрица, решение неоднородного уравнения (2.74) с начальным условием x (t0) -x ° записывается в виде Я X ° + j * Φ «1 (x) [Vi (t) 4-C / (t) 1 ди и (2,76) * (/) = Ф (/) Пусть X (/, t0) обозначает базовую матрицу, обладающую тем свойством, что она становится единичной матрицей для всех / 0 = /. X (/, 0 = X (/ 0. / 0) = E.
Другими словами, матрица X (/, / 0) является базовой матрицей, нормализованной к t0. Поэтому она называется базовой матрицей, нормализованной везде. Если фундаментальная матрица Φ (/) известна, нормализованная фундаментальная матрица определяется уравнением всюду X (L / 0) = Ф (/) Ф-1 (/ 0) — (2,77) Для стационарных систем матрица X (/, / 0) зависит только от разности t- / 0 (X (/, / 0) = X (/ — / 0)) и имеет вид. X (/ — / 0) = eA (‘~’ в \ где сим и Всего строк eA (1-1.) = E-h A (/ — / 0) 4- + jj-A2 (/ -10) 2 + … + «(/ — / 0)» + …. (2.78) л! Используя всюду нормированную матрицу, решение неоднородного уравнения (2.74) с начальным условием x (/ 0) = x ° записывается в виде x (t) = X (t-tQ) x ° + fX (t-c) [B (x) + Cu (x) l d *. (2,79)
Эта формула называется формулой Коши. Пример 2.7. Опишите систему с уравнениями X \ = * 2 «* 2 =» или. В матричной форме с уравнениями x = Al: + Be, где Используйте (2.78), чтобы найти нормализованную матрицу везде. с того времени — [«] N»] ……’- [«Я ….. Согласно уравнению Коши, решение неоднородного уравнения для jc (/ o) = x ° имеет вид Откуда T * (O = A + e-to) 4 + J </ — x) и (m) n, и T * 2 (0 = * ° + J * и (t) dx. «O Преобразование дифференциальных уравнений в обычные системы. Как правило, дифференциальные уравнения для одномерных и многомерных линейных стационарных систем всегда можно свести к обычным системам. Рассмотрим, как общие уравнения одномерной стационарной линейной системы сводятся к нормальной системе.
(Я) (Я — Я) (Я) (Я — Я) y + a, y 4 -… + apu = bn и + bn.t и + … + b0 и + (I) (I-1) + + … + c0 /. (2,80) Здесь для удобства коэффициенты справа пронумерованы в обратном порядке. Кроме того, есть выражение (2.80), которое включает в себя производную от входной величины и первого порядка / до /. Однако такие записи не нарушают общности. На практике, если порядок старшей производной входной величины меньше n и равен m и / k = bn, = … = bm + i-0 и c „-… = c, + 1 = 0. (2.80) можно преобразовать в обычную систему вида: *! = ** + а и -4-0, /, X2 = * 3 + + P2 / » (2,81) = + ap-1 «+ fl ^ i /» фут — я = ~ ^ + + Pn / » Я
Где коэффициент и муха определяются из соотношения: а0 = п — \ — я an-J = bJ- ^ an-h ~} ak>] ** ‘P ~~ Po = fe «0 / =» 0 / = J % Ip) y, + ••• +% (P) Y9 = bpl (p) ut — + — ••. + (P) Um -f + c9l (p) fi + + Cfl (p) ft или в более компактной форме, т т я t = 1 …. р. (2,59) / = -1 Где b ^ (p) и cj (p) — стационарные линейные Torus, многочлен от дифференциальных операторов с постоянными коэффициентами. Переход обеих частей (2.59) к изображению Лапласа дает систему алгебраических уравнений при нулевых начальных условиях ^ alf (s) Y, (s) = 2 ^, (s) (/, (s) + 2’i / WiW, i = 1 ….. p, (2.60) / «I / = -1 где Ky (s) = L \ yt (01, Ufls) = L \ u, (t) \ t Ft (s) -L | /, (/) |.
Для многомерных систем полезна матричная форма для описания уравнений. Представляя шествие (П) 1 7. » B (p) = 1A <(P) — / = ■. С «) — (P) J L ~ Y \ «Ям (P) -a, p (P)» , A (P) = ai (p) … arg «•» 1 си (п) … си (п) с91 (р) -. c9i (p) С их помощью (2.59) в матричной форме: A (p) y = B (p) и + C (p) /. (2,61) Точно так же вы можете написать (2.61) в матричном формате в образе Лапласа A (s) Y (s) = B (s) U (s) + C (s) F (s). (2,62) / —O, = o (N-I) «j; 1 (/)» -1 / = 0 / = () Продифференцируйте первое уравнение полученной системы и добавьте и вычтите выражение am 4- / справа. X = y-a, s-P0 / — + a, m + f- Учитывая второе уравнение системы (2.85), последнее уравнение можно записать в виде + <2 U)
Выполнение аналогичной операции над последующими уравнениями системы (2.85) дает: * 2 = * s + agi + Pr /. …………………….. (2 87) xn-i = * „+ яя_ | и 4 *?„ _ i /. Последнее уравнение (2.85) системы после дифференцирования принимает вид: / 1-1 п — ме xn- = Y-2n «» — «- / и -2i Pn-1- / ‘/ = 0, = 0 Или если / -f-I представлен /, <*> «(/)» A O) = Y-2j an-i и -21 & »- / f • (L> Замените формулу (2.84) вместо производной и добавьте справа Вычтите сумму 21 ap-k 21 из ^ (/) (/) (a * — / «+ /): / == 0 с /> Введены следующие обозначения. X \ = Y-ao «-W. * 2 = Y-» o «-? 0 f- H) (2,85) * h = Y * l = -n- \ (2 fr = 0 \ ‘(футы) y-2 «* — /» — 2 f / = 0 / • -0> i, a — I-2 x’ ft = 0 ft x 2 / = 0 an-h U-n— \ 2 2 &> — / f + 2 b ‘»+ 2 / — / — 0 l iоФ <* l- / «-2J» «- / <• (2.88) / -I / -I
В правой части выражения в скобках равны, и От 1 до (/) / • H / 2 aL-A 2 «- ° n a0 U + al-1 ‘a1M + ao» + 2 (a2 «+ 4» ft ^ o / -o ..h /. (Р-1) -f a0u) + … 4- a, U / I-1 «+ al-2» 4- •• 4-a0 u) = u (Ояо + … + (Л-1) + Oian_i) 4 — «(яЛ-1ао + fln-2« I + ••• + fli al_2) + … + Oiaflи = L — я (/) l — я — я = 2 M 2 * »» — / — * a * / = 0 * = J Как хорошо l-1 фут (/) l-i (/) l 1 / 2 2 Pw ‘= 2’ 2 al- / _ l • fr — O / «O j — O fc = o Таким образом (2.88) можно переписать как: L — I L — I / L — I — D = -2 ** ♦ «-2» 2-й — / — Ла * -bf4-а, — /) — l — I (n) 1-1-1 / 1-1 / — «2 a * + m + -ao)» -2 M 2 fc — + — * = 0 / –1 \ ft = 0 (Л) — / 2 Pft + + Л — Pe) /. (2,89> </ •) (/) Коэффициенты производных от u и f (/ ‘= 1, …, n) делаются равными нулю, а выражение для mi / представляется через an и j} соответственно.
n — 1— / bn- «. 0 = 0. 2 ba — / — l al- + = 0, / =! ….. n-I, * = 0 L — 1 an = b0-2 va-l • k — 0 I-1- / —Po = 0. 2 al — / — * + Pn- / = 0. / -Я, …, н-я, * = 0 я = Co-2 • (2,90) (2.89) принимает следующую форму n — 1 (2,91> x „-2 an-h xk + 1 + + M- * = о 2 * Ярко, (2.86), (2.87) и (2.9!) Система макияжа (2.81), рекурсивное соотношение (2.82) является первым уравнением из системы (2.90), и (2.83) <* system (2.85) здесь [„ A (секунды) > 1 м B (s) = %
Состоит из взвешенных функций управления, называемых матрицей импульсных переходов или взвешенной матрицы управления. Аналогично определяют импульсный переход или весовую матрицу возмущений w / (/) = Где wjf (/), …, w [, (/) — решения (2.59) многомерной системы. Здесь, Первенцами
Смотрите также:
Решение задач по теории автоматического управления
