Оглавление:







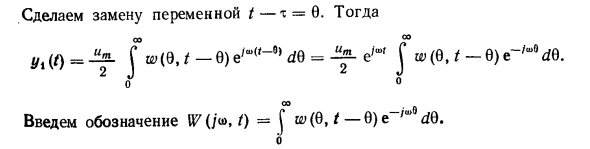

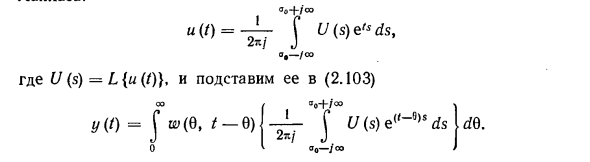








Нестационарные линейные системы
- Нестационарная линейная система Нестационарные линейные системы или линейные системы с переменными параметрами называются системами, описываемыми линейными дифференциальными уравнениями с переменными коэффициентами. Чтобы объяснить их, в дополнение к дифференциальным уравнениям можно использовать ранее введенные понятия, такие как передаточные функции, функции перехода и веса (импульсный переход), частотные функции и их характеристики. Кроме того, структурные диаграммы могут быть использованы для графического представления нестационарных систем.
Однако методы, основанные на структурном представлении, не так эффективны, как для стационарных систем. Правила преобразования структурных схем, установленные при исследовании стационарных систем, не применяются к структурным схемам нестационарных систем. Рассмотрим несколько способов описания одномерной нестационарной системы. Они могут быть обобщены для многомерных систем, как это было сделано при описании стационарных линейных систем.
Для линейных систем (как стационарных, так и нестационарных) действует принцип суперпозиции, и для простоты вход может быть ограничен для рассмотрения только одной системы. Людмила Фирмаль
Уравнение для одномерной нестационарной системы (объекта) с одним входом в общем случае можно записать в виде (N) . «(0 = — ^ — j U (s) e ds, 0, — / 00 Где U (s) = L {u (t)} и (2.103) / «Используйте -f / oe y (f) = j w (b, * —6) -j t / (s) e (‘-0) $ rfs £ / 0 O ^ a0— / 00 Если вы измените порядок интеграции, «• + /» t <*> f Jw (fl ./-9)e a0— / 00 v 0 Очевидно, что внутренний интеграл является передаточной функцией параметра U? Равен (S, /). Итак, мы можем написать о0 + / оо y (f) = — ΓU (s) W (s, t) e * ds. 2-й Дж Oo— / co Этот интеграл согласуется с обратным преобразованием Лапласа. Следовательно, если изображение выходной величины * / (/) выражается как Y (st t), Y (s, t) = W (s, /) U (s). (2,104)
Из этого уравнения видно, что параметрическая передаточная функция равна отношению выходной величины к изображению входной величины. Если вам известна параметрическая передаточная функция и изображение входной величины, определите изображение выходной величины из (2.104) и используйте таблицу или другой метод для поиска самой выходной величины. Если весовая функция известна, параметрическую передаточную функцию можно найти, используя ее определение (2.100). Однако это может быть легко определено дифференциальным уравнением.
- Напишем переходную линейную систему с дифференциальными уравнениями Q (p. T) y (t) = R (p, /) <(/). где Q (p, t) = a0 (/) p «+ a, (/) p» — * + … + «„ (/), H (P. 0 = bo (0 Pm + Lx (/) p + … + Lm (/). Тогда его параметрическая передаточная функция следует дифференциальному уравнению Q (S, /) <<, o + JB, + JL ^ L + … + 44 ‘v’ ds d / 21 </ sa ^ дт. 1 дн Q дн W (2,105) = R (s, /), 4 DTN л! DSN где Q = Q (s, /) = a0 (/) s «+ a, (/) ^ + … + au (0. R (s, f) = b0 (t) sm + bt (/) sm ~ l + … + bm (/) Дифференциальное уравнение параметрической передаточной функции (2.105) имеет тот же порядок, что и производная (2,106)
Системное уравнение. Решение такое же сложное, как и решение исходного уравнения. Поэтому рассмотрим один из приближенных методов решения уравнения (2.105). Перепишите в следующем формате: Q (s, t) W (s, t) = R (s, 0-й N {W (s. 0} «(2-107) где N {W {s, /)} = — f- + … + X V «[ds dl 2! Ds * dii + (2.108) n \ ds ‘dtn J’ Поиск решений в виде серий В приближении нулевого порядка -W0 (s »t) -R (s, t) / Q (s, t). (2,109) Это передаточная функция системы, коэффициенты которой были «заморожены».
Чтобы вычислить первое число поправок t (s, t), подставьте полученное нулевое приближение в правой части уравнения (2.107) и подставьте сумму нулевого приближения и первой поправки в левой части. Людмила Фирмаль
Далее про Wj (s, t) W, (s, t) = N {W0 (s, t)} / Q (s, /). (2,110) Аналогично для i-й модификации Wl (stt) = N {Wl. , (Stt)} / Q (STT). (2,111) Пример 2.8 Найти параметрическую передаточную функцию нестационарной системы. Это уравнение <* o V + (° i + α0V-b0 u. В этом случае Q (s, t) = a0s-J- «i — \ — at, R (s, t) = b0, dQ / ds = o0, d2 Q / ds1 = 0, … Уравнение (2.107) имеет вид Принять форму (Aos -} — a, + at) W (s, 0 = b0 + N {W (s, /)}. Где N \ W (s, 0} = a0dW / dl. На основании (2.109) и (2.110) 0-е приближение и первая поправка могут быть записаны как тт? 0 (с, 0 = -. 0 = — ^ — р. 0 1 » aus + a} + at ‘(uitS + а, + а /) 9 (2.111) можно использовать для расчета последующих поправок.
Однако, если a мало, вы можете ограничиться только первой модификацией. и «+ +» O * + a <* ■> b0 Y (, .O ^ IT. («■») +>, («. 0- ( ‘• Квазистационарная система. Такая система называется квазистационарной, если коэффициенты уравнения переходной системы (2.92) изменяются медленно. При описании квазистационарных систем широко используется метод коэффициента замораживания. Этот метод является приближенным и основан на коэффициенте «заморозка». В уравнении переходной системы переменные коэффициенты π, — (/) и bt (() являются передаточной функцией системы с фиксированным временем / «фиксированным коэффициентом», переходной системой с фиксированным временем t = t »
Равен аппроксимации функции нулевого порядка (2.109). Предполагается, что коэффициенты уравнений переходной системы изменяются медленно, если они слегка изменяются в процессе перехода (система является квазистационарной). Здесь под временем переходного процесса понимается минимальное время (после подачи одного импульса), когда абсолютное значение весовой функции системы с коэффициентом замерзания не превышает некоторого достаточно малого положительного значения. Если интервал времени, в течение которого рассматривается процесс квазистационарной системы, велик, изменение коэффициента уравнения может быть большим.
Затем, используя метод с фиксированным коэффициентом, весь временной интервал делится на несколько интервалов, каждый раз, когда система представляет собой постоянный коэффициент, равный значению переменного фактора в любой момент времени из рассматриваемого интервала. Описывается уравнением с Формула Коши. В нормальной форме Коши общий вид уравнения для одномерной или многомерной нестационарной линейной системы 2 atj (t) xj + V bu (t) uj + V cu (t) fh i = 1 ….. l, (2.112) / = I / = I / -I Или в матричной записи (2,113) Где x — это фазовый вектор, управляющий или главный вектор действия, а / — это вектор мешающего воздействия. Φ (0 обозначает основную матрицу уравнения l: = A (/) *, (2,114)
То есть матрица, столбцы которой образуют n линейно независимых решений уравнения (2.114). Далее матрица X (/, / 0) = Ф (ОФ «1 Базовая матрица нормализована везде. если Основная матрица X (/, / 0) известна. Решение (2.113) = при начальном условии x (/ 0) определяется по формуле Коши и x (t) = X (A / 0) n: 0 + j’X (f, i) | B (m) и <m) + c (x) f (x) 1 di. Это уравнение позволяет определить решение гетерогенного уравнения (2.113), если известна система из n линейно независимых решений однородного уравнения (2.114). Выходное значение и его производное значение в момент времени t.
При рассмотрении стационарных систем время подачи входного сигнала обычно считается отправной точкой. Поэтому в этих случаях предположим, что m = 0. В этом случае это не может быть сделано. Поскольку отклик нестационарной системы зависит не только от времени tm, отсчитываемого с момента подачи импульса, но и от самого значения m, весовая функция нестационарной системы-w времени приложения импульса t и момента t , Реакция-процесс на выходе системы-не происходит Перед подачей входного сигнала: Эффект не может быть до причины. так Если t <x, то w (t — x, x) = 0. (2,94) Это состояние называется состоянием физической осуществимости или состоянием физической осуществимости. ..
Для стационарных систем условие физической осуществимости w (t) = 0 для / <0 соответствует одному из условий, которым должна удовлетворять исходная функция. Соотношение между выходной величиной и входной величиной через весовую функцию выражается интегральной зависимостью. T Y (0 = J w (t-x, z) u (x) dx (2,95) — О или T y (t) = jw (t-xlx) u (x) dx. (2,96) Уравнение (2.95) получается в предположении, что входной сигнал подается в момент t = –oot, а уравнение (2.96) получается в предположении, что входной сигнал применяется в момент t = 0. вы.
Первое уравнение определяет установившееся состояние, а второе — переходный режим. Выведите эти уравнения. По определению w (t-m, m) является решением уравнения (2.93) с u (t) = 6 (/ -m) Q (p, ‘) w (t-x, x) = f (p, f) 5 (/ -m). Умножим u (j) dx с обеих сторон и интегрируем с m от -oo до oo. Затем, если вы получите коэффициент уравнения, который превосходит знак интегрирования (это возможно, поскольку он не зависит от m), и выполните обратную операцию интегрирования и дифференцирования: 00 секунд Q (pJ) (‘w (t-m, x) u (x) dx = R (py t) f U (x) b (t-X) dx. (2.97) -00 —00 Колорадо Из определения дельта-функции j n (t) 5 (/ -x) dx = u (t), следовательно, (2.97) можно переписать в виде Q (p, f) j w (t-m, x) и (x) dx = R (p, t) u (t). -CO
Из уравнений, полученных таким же образом, решение y (t) уравнения (2.93) для любого входного сигнала определяется интегрированием, если известна весовая функция. 00 y (t) = | w (от f до m, m) <(m) dx. (2,98) Это уравнение соответствует (2.95) в силу условия физической выполнимости (2.94). Предполагая, что входной сигнал подается в момент времени t = 0 (u <t) = 0 для / <0), получаем (2.96). Когда переменная m изменяется, весовая функция w (t-m, m) становится функцией одной переменной t в зависимости от параметра m и называется нормальной весовой функцией. Нормальная весовая функция определяет временную зависимость выходного значения системы, когда на вход в данный момент t подается один импульс.
При изменении переменной / это считается параметром — весовая функция w (t-m, m) является функцией одной переменной m и называется сопряженной весовой функцией. Сопряженная функция определяет зависимость отклика системы в фиксированный момент времени t от момента подачи одного импульса t. Передаточная функция. Передаточная функция tt нестационарной системы операторного типа? (P, t) определяется так же, как передаточная функция (операторная форма) стационарной системы и равна отношению оператора действия R (p, t) к его собственному оператору Q (p, t) вы. b7 (p, t) = R (p, t) / Q (p, t).
Понятие функции передачи изображения Лапласа W (s, t) требует уточнения. Это не может быть определено как соотношение между изображениями выходной и входной величины, потому что неясно, как рассчитать W (s, .0) в соответствии с заданным дифференциальным уравнением системы. Между прочим, не существует простой связи между передаточными функциями IX ‘(p, t) и IV (s, t), такими как передаточные функции W (p) и W (s) стационарной системы. Перейдем к определению передаточной функции W (s, /).
Для этого используйте физические свойства функции передачи частоты. Как известно, стационарная функция передачи частоты Физический смысл системы заключается в следующем: Модуль равен отношению амплитуды гармонических колебаний на выходе и входе системы, а его аргументом является фазовый сдвиг. Передаточная функция частоты W (ja) стационарной системы связана с передаточной функцией lF (s) соотношением Аналогичная связь должна существовать между передаточной функцией W (jio, t) частоты нестационарной системы и ее передаточной функцией W (s, /). Следовательно, как только передаточная функция W (ja, /) частоты определена, определение передаточной функции t) получается автоматически.
Как показано ниже, когда гармонический сигнал подается на вход нестационарной линейной системы, на его выходе устанавливается «гармонический» сигнал переменной амплитуды с той же частотой. Затем определите функцию передачи частоты W (ja> t t) как такую комплексную функцию, в зависимости от параметра t частоты, модуль которой равен отношению амплитуд гармоник. Вибрация на выходе и входе переходной системы, а аргументом является фазовый сдвиг. Для систем с весовой функцией w (t-m, m) это свойство имеет следующие свойства: и W (/ t t) = j w (0, t-0) e˜ / 0> 9 dQ. (2,99) о
Это соотношение принимается как определение передаточной функции частоты нестационарной линейной системы с весовой функцией w (t-t, t). Получить передаточную функцию tt ^ (s, t) из (2.99) W (s, t) = f w (0, t-0) e до s0 dQ (2,100) о Передаточные функции W (jat /) и W (s, t) называются параметрическими. Следовательно, частота параметра (весовая функция (w (t-t, t)) передаточной функции нестационарной линейной системы является функцией 1РЧ / 0), /), определяемой соотношением (2.99). Параметрической передаточной функцией нестационарной линейной системы (с использованием весовой функции w (t-t, t)) является функция W (s, t), определяемая соотношением (2.100).
Докажем, что * функция W (ja), t), определенная в (2.99), действительно обладает характеристиками передаточной функции частоты. Подайте гармоническую функцию u = itcosЫ на вход нестационарной линейной системы, используя весовую функцию w (t-m, m). Выражается как сумма a = U {+ u2 = 4-. 2 2 Использовать (2.95) T y (t) = j w (/ -X, x) и (x) dx — и для u = b, = t T Y, (‘) = j W (tdx. Измените переменную m = 0. После этого, SO 00 Y \ (0 ~ jw (9, f-c) e / w (f_c) d0 = e / lr) о Введено обозначение W (ju, t) = j * w (0, t-0) e ~~ ‘u, o40. Кроме того, последнее выражение y {(t) принимает вид Y1 (0 = W (K O ^ • (2101> Аналогично, если s = -y e ~ / a, t, Y r (0 = 0 — ^ — e «/ w /, (2.102) л * где о Γ (- / ω, 0 = шω (-0) e / aA ^ e,
Решения (2.101) и (2.102) могут быть переписаны в следующих форматах * /, (/) = ЛК0— = o-y-e «/ u + m (b> 0], где L (s. /) = | U7 (f0, f) |, Φ (u>, f) = arg tt? (/ К, /). Используя принцип суперпозиции. Выходное количество у Если u = um COS и> /, y = yi + y2 = ((u>, /) m mcos [co / + φ (ω, /) |. Поэтому на практике модуль номера функции (/ ©, /), определенный в (2.99), равен отношению амплитуды выходного и входного гармонических сигналов, а его аргументом является фазовый сдвиг. Установите связь между выходным значением изображения (Laplace) и входным значением. T Перепишите (2.95) y (t) = jw (/ -c, t) и (t) dt, используя изменение — и Переменная t-m = 6, в следующем формате: 00 y (t) = fw (e, / -Q) u (t-0) d0 (2,103) о Представьте входную величину, используя обратное преобразование Лапласа.
Смотрите также:
Решение задач по теории автоматического управления
