Оглавление:








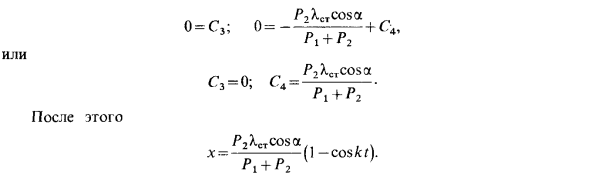

Общее уравнение динамики
- Соответствует балансу сил в каждой точке системы в соответствии с принципом Дарренва: механическая система, активная сила, объединенная сила реакции и сила инерции. Fk + Lk + Fk = 0, k = 1, 2, …, N, (23) Где Гк — активная сила. Rk — сила реакции связи; Фк — сила инерции точки. Умножение каждого из этих соотношений на возможное смещение точки 8rk на скаляр и суммирование всех точек в системе дает: ДFk ^ k + ДFk-8rk + ДФк • 8гк = 0. (24) Это общее уравнение динамики связанных систем. Обычно используется для систем с полной связью. * 5? * = 0- В этом случае (24) принимает одну из следующих форм (W) • «.» 0; (Ft-mta *) • 8rt = 0; D (^ — <4) ^ = 0, (25).
Поскольку сила инерции через ускорение aк относительно системы координат инерциальной системы координат выражается в следующем виде Φ (= -tkak = -tkkk, Где rk — радиус-вектор точки. Следовательно, согласно общему уравнению динамики, в любой момент системы с полной связью сумма основной работы всех активных и инерционных сил точки системы допускается связью Ноль с любым возможным движением. Общее динамическое уравнение (24) часто называют унифицированным принципом Даламбы-Лагранжа. Это также называется общим динамическим уравнением.
Может случиться, что точки материальной системы резко меняют свои скорости за весьма короткий промежуток времени, но система за тот же промежуток времени не меняет заметно своего положения. Людмила Фирмаль
В случае равновесия системы, если все силы инерции системы указывают на ноль, мы переходим к принципу статического возможного смещения без доказательства достаточности равновесия системы. Уравнениям общей динамики могут быть даны другие эквивалентные формы. Выявление скалярного произведения векторов можно выразить как: £ + ® „) Sy + (A, + Φ,.) 6 -.] — 0. Где xk, yk, zk — координаты k-й точки в системе. Учтите, что проекция сил инерции на оси координат за счет проекции ускорения на эти оси выражается следующей зависимостью: F * x = ~ тках = -тхх; Fku = -tkaku = -tkuk, F4; = -tkakg = -mkzk, общее уравнение для динамики дано в виде £ [(Ffc, -mjkxJk) 8xlk + (fi, -Wl | kA) 8 No. + (Fte-m) tfJk) 8zjk] = 0. (25 ‘).
В таком виде оно называется общим уравнением динамики в аналитическом виде. Общие уравнения для динамики систем, подверженных голономным и идеальным неразрывным связям, дают полную информацию о поведении таких систем. Это похоже на это. Вы можете получить полную систему дифференциальных уравнений о том, как равновесное состояние системы получается из принципа возможного смещения. Вывод этих уравнений требует использования обобщенных координат и обобщенных концепций сил. Предположим, у вас есть система, которая зависит от голономного, идеального, неизданного соединения.
Предположим, что положение в пространстве определяется обобщенными координатами qt, q2, …. q „, поскольку степень свободы равна n. Радиус-вектор каждой точки системы в общем случае нестационарных соотношений равен Обобщенные координаты и время, т. Е. ^ = M * (? 1, qz, nn, 0. (26) Потому что время считается неизменным. После подстановки (26) в общее динамическое уравнение (25) и изменения порядка сумм k и i получается следующее. к. (27) Используйте активную силу O, обобщенную силу O и силу инерции 21F ‘. (28) 4 = 1 * ‘? * = 1 001 Из (27) получите общее динамическое уравнение в следующем формате: Z (e (+ e} φ,) 8 ?. = ° — (29) Обобщенные координаты системы независимы. Эти изменения координат не только независимы, но и необязательны.
Предполагая, что только одна из обобщенных вариаций координат не равна нулю, а все остальные равны нулю, (29) дает следующую условную систему: 0 (+0! Φ) = 0, r = 1, 2, … и т. Д. (30) Условие (30) называется принципом Даламбера системы и выражается обобщенной силой. Условие уравнения для системы b следует (30), = 0, α = 1, 2, …, n, если сила инерции точки системы и, следовательно, обобщенная сила инерции, равна нулю. При использовании общих динамических уравнений необходимо уметь рассчитывать основную работу сил инерции системы при возможных смещениях. Для этого используется формула, соответствующая полученной работе начальной школы Для нормальной мощности.
- Рассмотрим приложение к силе инерции твердого тела для определенного движения. Поступательное движение. В этом случае тело имеет три степени свободы и принудительно соединено, поэтому может выполняться только поступательное движение. Движение тела, которое обеспечивает связь, также является поступательным движением. Инерционная сила при переносе уменьшается до результирующего Ф * = -Мас = -Ма. Для суммы основной работы силы инерции на возможность поступательного движения тела, ггйгй = = Φ * 8 8s = * * -8r = -L / d-8g, Где 8gs = 8g — возможное смещение центра тяжести и любой точки тела, потому что переводимое смещение одинаково во всех точках тела. Ускорение такое же, то есть как есть. Когда тело вращается вокруг фиксированной оси. Тело в этом случае имеет одну степень свободы.
Он может вращаться вокруг неподвижной оси Oz. Возможные перемещения, которые возможны благодаря наложенному соединению, такие же, как и вращение тела на базовый угол 8 (когда центр тяжести выбран в качестве центра торможения). Сумма основных сил инерции возможных инерционных перемещений на плоскости является основной работой главного вектора сил инерции = -массовая работа возможного движения центра масс и основной относительно оси Cz через центр масс Основной момент инерции общего вращательного движения сводится к работе элемента.
Следовательно, в этом случае ось ротора будет оставаться направленной на одну и ту же звезду и для наблюдателя, находящегося на Земле, она будет следовать за звездой в ее суточном движении. Людмила Фирмаль
В этом случае ненулевую базовую работу можно выполнить, только проецируя главный момент инерции на ось Cz, т.е. L $, = -JCze. Так что в рассматриваемом случае, ZФ * ’8г * = Ф-5гс + 1, ??, 8 , При повороте на базовый угол 8 ; z2 = 2Zcos «p. Изменяя эти зависимости, есть: 8.V] = Zcos ; Sz2 = -Zsin ; 8z2 = -2Zsin , оно становится следующим. — (Z1 + Zsinq>) «e2Z cosip-Z’sinip -cZsinipcosip -gsin 3-PTg -Qtg = официальный 1 приложение Система, предполагая, что координата FL-z постоянна, нам нужно вычислить инерцию смещения точки_ при изменении координаты x.
Поскольку мы дали 6x возможных движений в направлении увеличения координаты x, уравнение (b) 0! = O, сила тяжести Pt, P2 перпендикулярна возможному движению, сила упругости (одна добавляется к нагрузке, другая изначально равна, но направление противоположно), к призме точки крепления пружины ) В сумме приведем базовую работу, равную нулю с константой s. Для каждой обобщенной силы инерции -F18l-Ф2.8й. P, x + P2 (от cosa + x) Q \ * ‘= — = — (Ф 、 + Ф2 、) = —————! ~ = 8 раз Призма инерции Доска У нас есть @ P2sina83 — F6s Суммированная река Сена По возрастающей координате z всегда вычисляется по формуле.
Если s рассчитывается из положения статического равновесия нагрузки B, поскольку сила упругости F = cX = c (XCI + 3), HS — статическое растяжение пружины под действием силы тяжести. Равновесие. В положении Статика удовлетворяет условию Равновесие. Обобщенные Инерция у нас есть интеграция (A) Получите следующее Константа С, Synaf + cj, условия Со второй интеграцией x = -L ^^ lcoskt + Cjt + Cf — (S-h-xcosa), г Где Ф2 — проекция инерции нагрузки B на ось.
Подставьте полученное значение обобщенной системы нагнетания для дифференциального уравнения. Исключите следующее выражение для s из второго выражения: P2 [P | + P2 (1-интеграция (r), получить s <iCoskt + CiSinkt. А С2 определяется начальными условиями Производная (г ‘), s = -Clksmkt + C2kcoskt. Из 1 = 0 (r ‘) и (g «) -1 с = C1; C2 = 0. После этого Заменить следующую разницу Константы C3 и C4 определяются с использованием 1 = 0, x = 0, A = 0. Из (d ‘), (d «) и начальных условий.
Смотрите также:
Задачи по теоретической механике
| Вычисление обобщенных сил | Уравнения Лагранжа |
| Условия равновесия системы | Тождества Лагранжа |
