Определение. Функция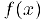 
называется непрерывной в точке 
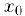, если она определена в некотором интервале, содержащем эту точку и существует предел 
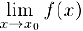, равный значению функции в точке 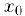, т. е.
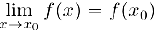
Приведем еще одно определение непрерывности функции, равносильное приведенному. Пусть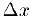 
— приращение аргумента (малое положительное или отрицательное число) в точке 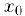. Величина
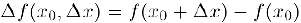
называется приращением функции 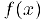в точке 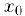. Тогда, очевидно, функция непрерывна в точке хо тогда и только тогда, когда
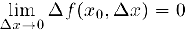
Если предел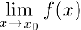 
не существует или равен бесконечности, либо указанный предел существует и конечен, но не равен значению функции в точке 
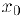или функция неопределена в этой точке, то будем говорить, что функция 
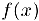разрывна в точке 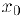или. иначе, 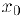— точка разрыва данной функции.
Перечислим теперь основные, свойства непрерывных функций, следующие из соответствующих свойств пределов (§4. пункт 2).
1) Если функции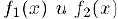 
непрерывны в точке ха, то в этой же точке непрерывны и функции
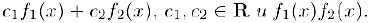
Если, кроме того, в области определения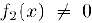 
. то непрерывной является также и функция 
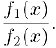. Наконец, если в области определения 
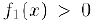, то непрерывна и функция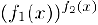 
Для доказательства достаточно использовать свойство 7) предела функций и предел (3) из пункта 2, §4.
2) Если функция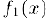 
непрерывна в точке 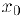, а функция 
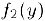в свою очередь, непрерывна в точке 
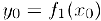, то композиция функций 
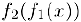непрерывна в точке .
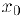Здесь достаточно сослаться на свойство 2) предела композиции функций (пункт 2, §4).
3) Если функция 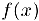непрерывна в точке 
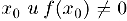, то в некотором малом интервале, содержащем точку 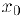данная функция сохраняет знак значения 
.
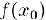Действительно, выбрав число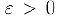 
столь малым, чтобы 
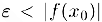, мы по определению непрерывности можем указать 
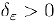, для которого
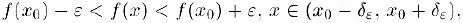
что и доказывает данное свойство, так как по выбору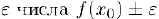 
с имеют знак значения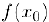 
По аналогии с односторонними пределами мы можем также ввести понятие односторонней непрерывности функции. А именно, функция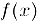 
, определенная в полуинтервале 
называется непрерывной слева (справа) в точке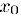 
, если существует левосторонний (правосторонний) предел 
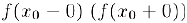, равный значению функции в точке 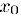. Из свойства 1) предела функции (§4, пункт 2) следует, что для непрерывности функции 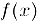в точке 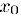необходимо и достаточно, чтобы она была непрерывной слева и справа в этой точке и 
.
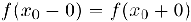Функция называется непрерывной на промежутке числовой оси, если она непрерывна в любой точке этого промежутка, причем, если промежуток содержит граничные точки, то под непрерывностью в них понимается соответствующая односторонняя непрерывность.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
