Оглавление:
Параметризация целевой функции
Рассмотрим алгоритм метода взвешенных сумм на примере параметризации целевой функции для задачи ЛП с одним критерием (см. разд. 5.2).
Исходная задача имеет вид
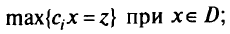
задан вектор изменения 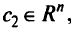 , который определяет изменения координат целевой функции; вводится параметризованный (суммарный) градиент целевой функции
, который определяет изменения координат целевой функции; вводится параметризованный (суммарный) градиент целевой функции 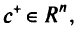 т.е.
т.е.
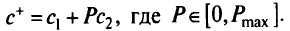
Отсюда находим последовательность параметрически оптимальных крайних точек (и ребер) при изменении 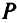 от 0 до
от 0 до 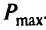 . Точка
. Точка 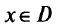 называется параметрически оптимальной, если она максимизирует величину
называется параметрически оптимальной, если она максимизирует величину 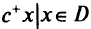 для некоторого значения
для некоторого значения 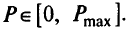 . При использовании метода взвешенных сумм вводится выпуклая комбинация векторов
. При использовании метода взвешенных сумм вводится выпуклая комбинация векторов
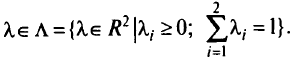
Тогда
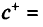
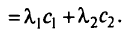
Между обоими подходами существует прямая связь:
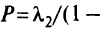
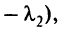
так как
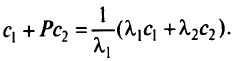
Однако в первом случае вектор  не достигает вектора
не достигает вектора 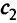 (только к нему стремится), во втором —
(только к нему стремится), во втором — 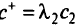 при
при 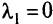 .
.
В поставленной задаче требуется определить критические значения 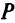 или
или 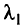 и
и 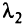 , при которых новые базисы (крайние точки) становятся параметрически оптимальными (т.е. происходит смена базиса). Задача решается в три этапа:
, при которых новые базисы (крайние точки) становятся параметрически оптимальными (т.е. происходит смена базиса). Задача решается в три этапа:
- Находим допустимую крайнюю точку из области
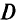 — для решения симплекс-методом задачи ЛП
— для решения симплекс-методом задачи ЛП 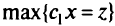 при
при  .
. - Решаем задачу ЛП
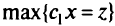 при
при  — получаем исходный параметрически оптимальный базис.
— получаем исходный параметрически оптимальный базис. - Заменяем градиент
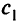 на
на 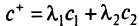 и находим остальные параметрически оптимальные базисы (крайние точки), варьируя значения
и находим остальные параметрически оптимальные базисы (крайние точки), варьируя значения 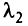 от 0 до 1. При этом строка
от 0 до 1. При этом строка
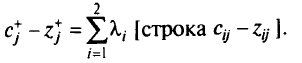
В процессе решения могут быть следующие варианты:
- Все небазисные элементы
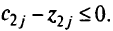 . Отсюда — исходная точка уже оптимальна.
. Отсюда — исходная точка уже оптимальна. - Существуют внебазисные положительные элементы
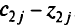 ,
,
т.е. найдется выпуклая комбинация, при которой 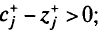 ; небазисную переменную, соответствующую этому элементу, переводим в базис.
; небазисную переменную, соответствующую этому элементу, переводим в базис.
Берем тот элемент 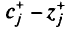 , который первым стал больше 0 при увеличении значения
, который первым стал больше 0 при увеличении значения 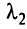 .
.
Ближайшим большим критическим значением 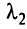 будет
будет
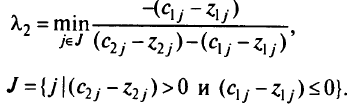
Значение 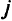 , при котором дробь минимизируется, указывает на небазисную переменную, переводимую в базис, чтобы продолжить параметризацию по
, при котором дробь минимизируется, указывает на небазисную переменную, переводимую в базис, чтобы продолжить параметризацию по 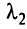 .
.
Задача:
Для
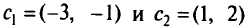
рассмотрим задачу параметрического ЛП с ограничениями
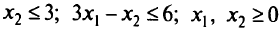
(рис. 5.19).
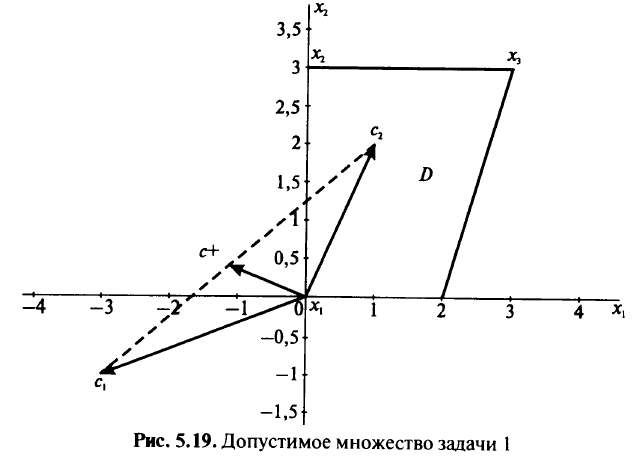
Решение:
Оптимальную исходную симплекс-таблицу (табл. 5.13) задачи ЛП
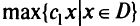
дополним строкой 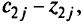
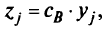 где
где 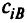 — координаты вектора
— координаты вектора 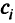 стоящие в базисных
стоящие в базисных
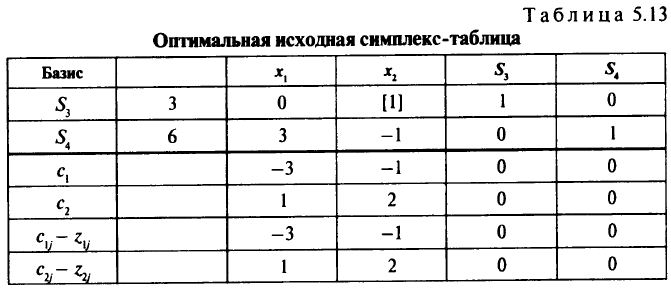
столбцах; 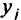 — элементы
— элементы 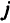 -го столбца матрицы. Здесь
-го столбца матрицы. Здесь
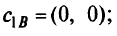
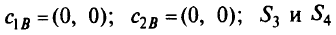
слабые переменные.
Для небазисных переменных
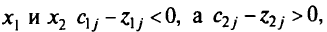
т.е. множество
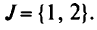
Критическое значение:
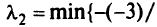
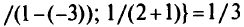
при
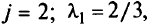
переменную  надо перенести в базис (в таблице помечен генеральный элемент);
надо перенести в базис (в таблице помечен генеральный элемент);
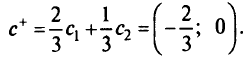
Вектор  ортогонален ребру
ортогонален ребру
строка
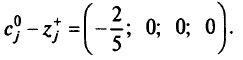
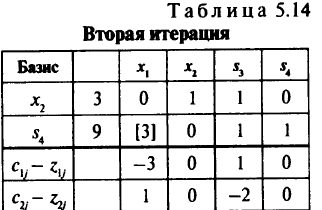
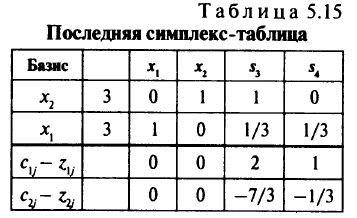
Получаем табл. 5.14.
Здесь
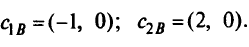
Только для столбца 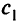 удовлетворяются условия
удовлетворяются условия
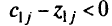
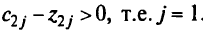
Новое критическое значение
переводим
в базис;
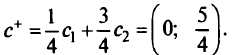
Вектор 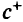 ортогонален ребру
ортогонален ребру
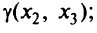
строка
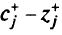
имеет вид
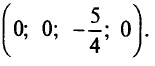
Вводим в базис  получаем
получаем
Здесь
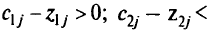
процесс завершен.
В процессе ршения получили следующие подмножества множества 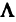 , относящиеся к различным параметрически оптимальным крайним точкам и ребрам:
, относящиеся к различным параметрически оптимальным крайним точкам и ребрам:
Задача:
Методом взвешенных сумм проанализировать задачу МКЛП:
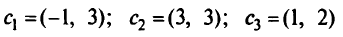
при ограничениях
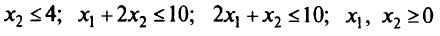
(рис. 5.20).
Решение:
В данном случае суммарный градиент целевой функции
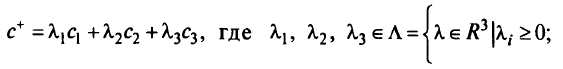
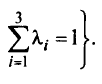
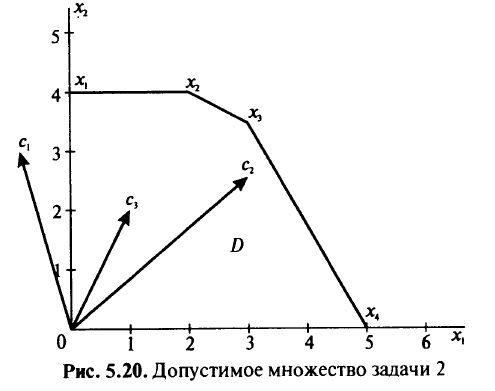
Найдем подмножества Ё, принадлежащие различным параметрически оптимальным крайним точкам и ребрам. Решим задачу ЛП
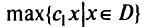
и добавим в полученную оптимальную симплекс-таблицу строки для
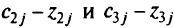
(табл. 5.16). После решения задачи ЛП мы имеем начальную параметрически оптимальную крайнюю точку
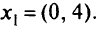
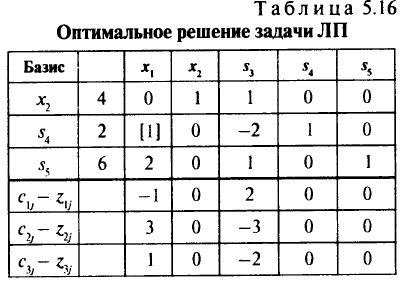
Анализируем строку
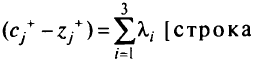
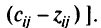
Поскольку небазисные элементы строки 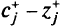 должны быть неположительны в параметрически оптимальной крайней точке для всех
должны быть неположительны в параметрически оптимальной крайней точке для всех 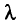 из подмножества
из подмножества 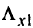 , соответствующего точке
, соответствующего точке 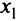 , то имеем
, то имеем
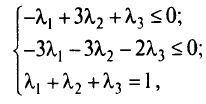
где
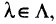
или. учитывая
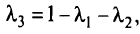
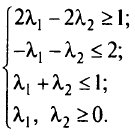
Из этой системы получили
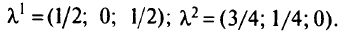
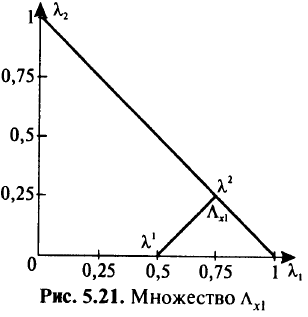
Множество 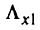 изображено на рис. 5.21.
изображено на рис. 5.21.
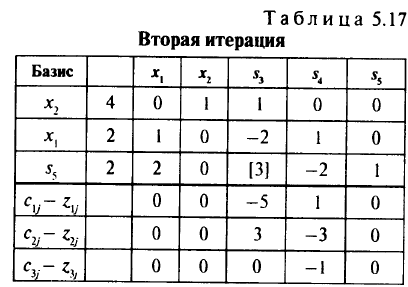
Переводим 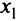 в базис и переходим путем замещения методом Жордана в точку
в базис и переходим путем замещения методом Жордана в точку 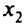 = (2, 4) (табл. 5.17).
= (2, 4) (табл. 5.17).
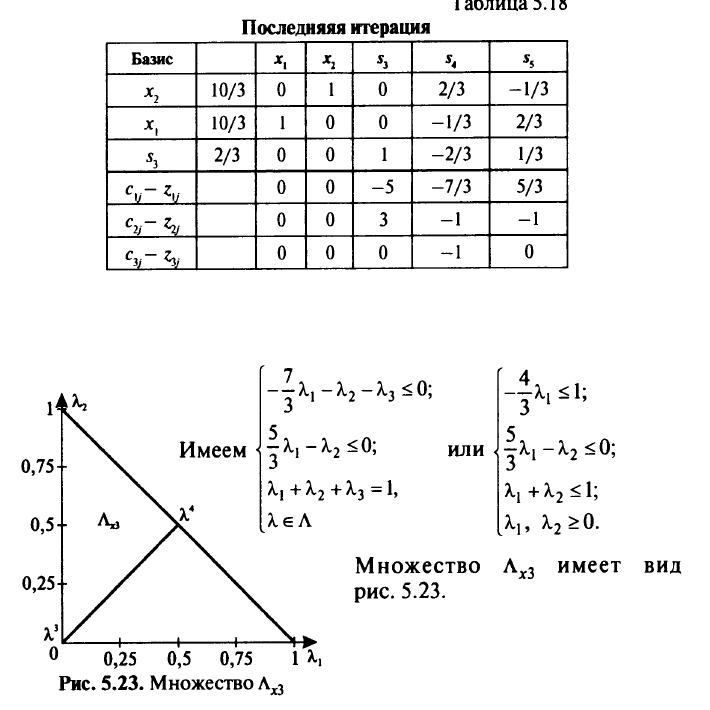
Для определения 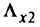 составим систему неравенств:
составим систему неравенств:
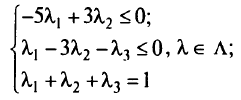
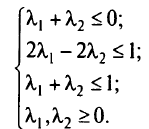
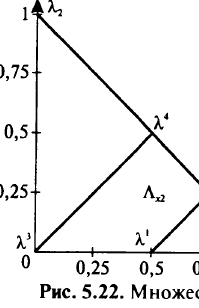
Решив систему, получим
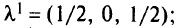
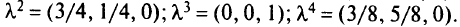
Множество 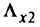 изображено на рис. 5.22. Далее переходим в точку
изображено на рис. 5.22. Далее переходим в точку
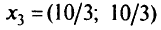
(табл. 5.18).
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
