Задача №3.
Ползун 
приводится о движение посредством нити, наматывающейся на шкив радиуса 
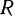. Определить скорость ползуна в зависимости от расстояния 
, если угловая скорость шкива равна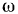 
(рис. 3).
Решение:
В рассматриваемом случае легко устанавливается простая зависимость
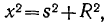
где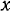 
— расстояние .ползуна от центра шкива; 
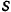— длина отрезка нити 
(
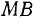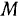— точка касания нити со шкивом). Это соотношение выполняется в любой момент движения и его, конечно, можно ‘Продифференцировать по времени:
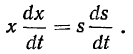
Но здесь скорость изменения величины 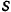, то есть
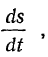
остается неопределенной, и мы не получаем решения задачи. Приходится искать другую величину, изменение которой известно, и другую зависимость, связывающую эти величины. Если в качестве такой величины принять длину участка нити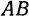 
, которую обозначим через 
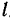, то
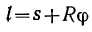
или
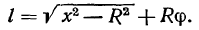
Это соотношение остается справедливым во все время движения, а потому, дифференцируя его, будем иметь
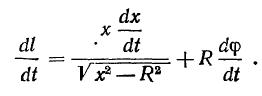
Здесь
а потому
откуда
и после подстановки
Скорость изменения величины 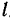теперь уже является известной величиной
и мы легко получаем, что
Применение подвижных осей (полярная система координат, естественные оси и т. д.) дает возможность глубже понять некоторые свойства движения. Вместе с тем при этом возникают и некоторые новые затруднения, которые не встречались при изучении движения в прямоугольных декартовых осях При анализе таких движений ‘применяются как геометрические, так и аналитические методы исследования.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
