Оглавление:



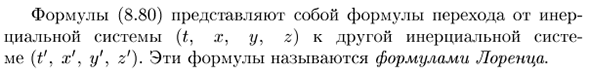

Преобразования Лоренца пространства E4
- Преобразование Лоренца пространства Эль 3й Система координат Галилея псевдоевклидова пространства Ef ± 3h Фонд е ^. В такой системе координат квадрат интервала s2 (x) равен Имеет вид (8.71), а метрическая тензорная матрица {gij] имеет вид J = 10 0 0 0-100 0 0-10 0 0 0-1 3,72) Переход к новой системе координат Galileo с базисом e ^
- Найти условие, что коэффициент b1 должен удовлетворять. В форме (8.72) и использовать формулу d ^ y-b \, bJ, gij преобразования Получаем координаты метрического тензора, следующую систему уравнений Уравнение для определения коэффициента b \, матрица B преобразования Базисные векторы (см. (8.73); кроме того, индексы r и r ‘
Матрица B преобразует базисные векторы. с того времени е * = 4 е * (8,73) И метрическая тензорная матрица (gi> j>) базиса е ^ Людмила Фирмаль
Значения 0, 1, 2 и 3 (см. (8.71)): KJ ~ E 3 E W = 0, (8,74) а = 1 w = f «! for ^; = ^ y, /? ‘= 1,2, с. a = i (0 равно 7 ‘//?’, Соотношения (8.74) можно описать в матричной форме. Для этого Рассмотрим матрицу 5 * с матрицей B. Изменить знак последних трех столбцов из B И последующее перемещение. Ясно отношения (8.74) Это может быть написано в следующем формате:
B * B = J, (8,75) Где матрица J определяется соотношением (8.72) (для сравнения Предположим, что матрица ортогонального преобразования C евклидова Пространство удовлетворяет соотношению C C = /. Где / это единица. Матрица). det B * = -det B и det J = -1, поэтому соотношение (8.75) Следовательно, det B * B = det B * det B = — (det BJ = -1 дет B = ± 1. (8,76)
Предположим, что мы показываем множество всех общих преобразований L Минковский аренда помещений. Из этих общих преобразований Выберите преобразование для преобразования каждого вектора От T + до вектора, который также принадлежит T +. Все Формирование обычно называют преобразованием Лоренца пространства Ef ^ 3s, обозначается символом L ^.
Генеральное преобразование Лоренца с det B = + 1 Назовите так называемый соответствующий класс преобразования Лоренца L +. Некорректный класс преобразования Лоренца L_ По связи det B = -1. Примером такого преобразования является Действует как отражение трех пространственных осей: x1 = 19 ‘9 H7 H Ю, Ю Ю, Ю Ю.
- Пусть B будет любой неподходящей матрицей преобразования Лоренц и Р — только что рассмотренные матрицы отражения. очень Любые неправильные продукты преобразования видны, Будет уникальным преобразованием из рассмотренных отражений рисa B ‘= RV. Где P2 = P • P = /, где / — единичная матрица. B = P2B = P (PB) = PB ‘. Таким образом, неуместное преобразование Лоренца.
Является ли продукт некоторой подходящей конверсии Отражение матрицей B ‘и матрицей R Пересечение множеств L ^ и L + обозначается L +. Несколько групповых свойств множества L, L ^, L + и L + поставляются Описано в следующей главе. В заключение найдите неизменное L + преобразование Координаты х2 и 3.
Очевидно, это будут L + 2D преобразования. Людмила Фирмаль
Псевдоевклидово подпространство с координатами x ° и x1 Квадрат интервала задается формулой (x0J- (x1J. Этот случай описан в формуле экзамена (8.74). получить (B ° 0, J-Ш2 = 1, b ° 0, b ° v-b1, b \, = 0, (8,77) б ^ / Щ, = /? Предполагая, что из (8.77) находим Для коэффициента ^ матрица базисного преобразования вектора B Например, отбросьте ei, B2 и ez в их базисные векторы, e ^, B2 ‘и ez ^. 1
В этих выражениях символ выбирается из предварительных условий Слой Лоренца до класса L +. Не вдаваясь в детали расчета Напишите окончательную формулу преобразования координат: х1- / хх ° 0 / _ x ° — / 3×1 Х- X1 ‘= х1 = х1 х3 ‘= х3. 0,78 долл. США) Соотношение (8,78) х ° = с? , X1 = x, x2 = 2 /, x3 = = z, x ° = = ct ‘, x1 = x;, x2 = y’, x3-zl. Далее формула (8,78) Перепишите так: t- ^ x, -set + x т ‘= X = = y, z = z. 3,79) Здесь физический смысл константы p уточняется.
Предположим, что Точка P фиксируется в системе координат (t ‘, x’, 2 /, z7). Средства, Это означает, что время t изменяется, а пространственные координаты x, y, z изменяются. Эта точка постоянна. Проблема поведения точки P относительно По поводу системы (?, X, 2 /, r). Дифференцируя последние три уравнения, Учитывая уравнение (8.79) и dx ‘= dy’ = bb7 = 0, 0 = -f3cdt + dx dx dy dz -, 0 = dy, 0 = cb.
Так что = /? S, — = 0, — = = 0 В результате все точки P фиксируются в системе координат nat (t ‘, x; 2 /’, z ‘) (отсюда вся эта система координат), Движение против системы (?, X, y, z) с постоянной скоростью v = (3x, в направлении оси Ox. Итак / 3 = v / c, где ^ — скорость системы (tf, x », ^ y7, z;) Относительно системы (x, 2 /, 2,?). Так как 0 <v <c, 0 </? <1. Перепишите следующую формулу (8.79). f = (8,80) Уравнение (8.80) является уравнением от неактивности к переходу Социальная система (?, X, Y, Z) к другой инерциальной системе Я (?, X ‘, y’, z ‘). Эти формулы называются формулами Лоренца.
Смотрите также:
| Понятие псевдоевклидова пространства и метрического тензора псевдоевклидова пространста | Тензор момента инерции |
| Галилеевы координаты. Преобразования Лоренца | Законы композиции |
