Оглавление:
Рассмотрим график функции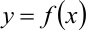 
на рисунке 5.2. Исследование функции включает в себя помимо других вопросов определение интервалов возрастания и убывания функций, а также поиск точек максимума и минимума (точек экстремума). Геометрический смысл производной позволяет определить эти особенности функции.
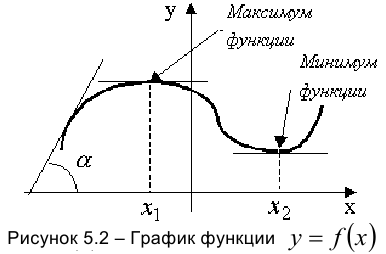
1. Функция является возрастающей на тех интервалах, где её производная положительна. На рисунке 5.2 это интервалы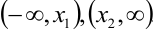 
. На указанных интервалах угол наклона касательной к графику функции острый, следовательно, 
.
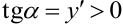2. Функция убывает на интервалах, где её производная отрицательна, т.е.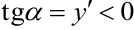 
. На рисунке 5.2 интервал убывания функции (
,
).
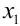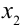Необходимым условием существования экстремума функции является равенство нулю её производной или отсутствие производной в некоторых точках, которые называются критическими. Чтобы в этих точках существовал экстремум функции должно выполняться достаточное условие экстремума: если при переходе через критическую точку знак производной меняется с «плюса» на «минус», то в данной точке имеется максимум функции; если производная меняет знак с «минуса» на «плюс», то в такой критической точке функция имеет минимум. Для существования экстремума, кроме того, функция должна быть непрерывной в критической точке.
На рисунке 5.2 в точке 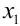функция имеет максимум, в точке 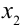— минимум. Касательная к графику функции в этих точках параллельна оси аргумента.
Если стоит задача определения наибольшего и наименьшего значения функции на отрезке, то её нужно решать в следующей последовательности:
- определить критические точки;
- вычислить значения функции в критических точках и на концах отрезка;
- выбрать из найденных значений функции наибольшее и наименьшее.
Вторая производная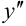 
применяется для определения интервалов выпуклости и вогнутости графика функции.
Принцип определения таких интервалов показан на рисунке 5.3. Точка, лежащая на границе между выпуклостью и вогнутостью, называется точкой перегиба
Пример выполнения задания
Пример:
Найти наибольшее значение функции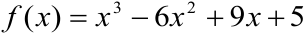 
на отрезке [0;4].
Решение:
Найдём производную, а затем критические точки.
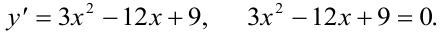
Корни уравнения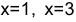 
являются критическими точками для данной функции, они входят в заданный отрезок. Вычисляем значения функции в критических точках и на концах отрезка:
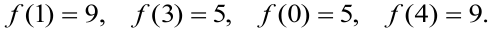
Сравнивая полученные значения, делаем вывод, что наибольшее на отрезке значение функция принимает в точках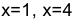 
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
