Оглавление:
Работа силы на конечном пути
Для определения работы силы 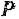 па каком-либо конечном перемещении
па каком-либо конечном перемещении 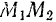 (рис. 208) ее точки приложения разобьем это перемещение на
(рис. 208) ее точки приложения разобьем это перемещение на 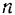 перемещений, каждое из которых в пределе (при
перемещений, каждое из которых в пределе (при 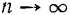 ) переходит в элементарное. Тогда работа
) переходит в элементарное. Тогда работа 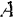 силы
силы 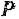 на конечном перемещении
на конечном перемещении 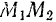 будет равна пределу суммы ее элементарных работ на всех бесконечно малых участках данного перемещения, и пользуясь формулами (187) и (189), получаем для нее следующие выражения:
будет равна пределу суммы ее элементарных работ на всех бесконечно малых участках данного перемещения, и пользуясь формулами (187) и (189), получаем для нее следующие выражения:
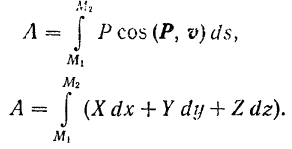
Работа любой силы на любом конечном перемещении ее точки приложения равна взятому вдоль этого перемещения интегралу от элементарной работы.
Пределами интегралов в формулах (190) и (191) являются значения соответствующих переменных интегрирования в точках 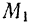 и
и 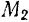 .
.
Если точка 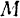 приложения силы перемещается по криволинейной траектории, то интегралы берутся вдоль соответствующей дуги
приложения силы перемещается по криволинейной траектории, то интегралы берутся вдоль соответствующей дуги 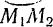 этой траектории, т. е. являются криволинейными интегралами.
этой траектории, т. е. являются криволинейными интегралами.
Если модуль касательной составляющей 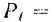
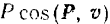 силы есть величина постоянная, то из формулы (190) будем иметь:
силы есть величина постоянная, то из формулы (190) будем иметь:
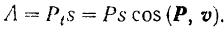
В частности, это всегда имеет место при прямолинейном движении точки под действием постоянной по модулю и направлению силы.
Работа постоянной силы при прямолинейном перемещении ее точки приложения равна произведению модуля силы на длину пути, пройденного ее точкой приложения, и на косинус угла между направлениями силы и перемещения ее точки приложения.
Если направление постоянной силы совпадает с па-правлением перемещения точки ее приложения или прямо противоположно направлению движения последней, то
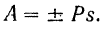
Формула (193) применима не только в случае прямолинейного перемещения точки приложения постоянной силы, но и в случае ее криволинейного движения, если только эта сила все время направлена по касательной к траектории ее точки приложения.
Работа силы имеет, очевидно, следующую размерность:
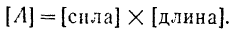
Так как в технической системе единиц сила измеряется в килограммах, а длина — в метрах, то работа в технической системе единиц измеряется в килограммометрах (кГм).
В системе СИ сила измеряется в ньютонах и длина в метрах, поэтому в этой системе за единицу работы принимается работа силы в \ н на пути, совпадающем с направлением силы, в 1 м. Эта единица работы называется джоулем (дж).
Найдем зависимость между килограммометром и джоулем. Ранее (стр. 242) было найдено, что сила в
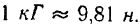
Следовательно,
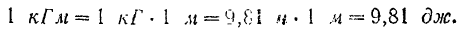
Один килограммометр равен 9,81 джоуля.
Пример задачи:
Тело совершает поступательное прямолинейное движение по закону 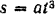 , где
, где 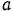 — некоторый постоянный коэффициент. Модуль силы сопротивления среды
— некоторый постоянный коэффициент. Модуль силы сопротивления среды 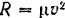 , где
, где 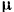 — коэффициент сопротивления среды и
— коэффициент сопротивления среды и 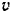 —скорость тела. Какую работу надо затратить на преодоление сопротивления среды при перемещении тела из состояния покоя на расстояние
—скорость тела. Какую работу надо затратить на преодоление сопротивления среды при перемещении тела из состояния покоя на расстояние 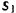 ?
?
Решение:
Тело принимаем за материальную точку 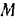 . Прямую, по которой движется эта точка (центр тяжести тела), принимаем за ось
. Прямую, по которой движется эта точка (центр тяжести тела), принимаем за ось 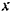 , направив ее в сторону движения топки (рис. 209).
, направив ее в сторону движения топки (рис. 209).
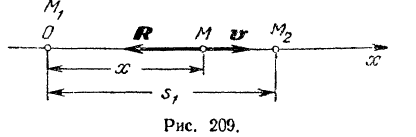
Начало координат будет совпадать с начальным положением 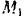 , точки (как видно из закона ее движения: при
, точки (как видно из закона ее движения: при 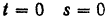 ).
).
Найдем работу силы 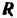 сопротивления среды, воспользовавшись для этого формулой (191):
сопротивления среды, воспользовавшись для этого формулой (191):
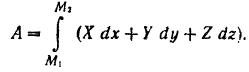
Так как сила 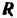 сопротивления среды всегда направлена в сторону, противоположную движению тела, то ее проекциями на координатные оси будут:
сопротивления среды всегда направлена в сторону, противоположную движению тела, то ее проекциями на координатные оси будут:
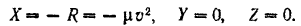
При выбранном направлении оси 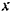 абсцисса точки
абсцисса точки
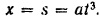
Элементарное приращение этой координаты
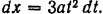
Скорость точки
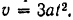
Подставляя найденные выражения в формулу (191), получим
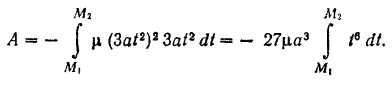
Так как подынтегральное выражение является функцией времени, то пределы интегрирования должны соответствовать значению этой переменной в точках 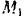 и
и 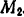 . Положению
. Положению 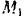 точки соответствует время
точки соответствует время 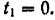 Момент
Момент 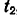 , соответствующий положению
, соответствующий положению 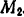 точки, находим из закона ее движения:
точки, находим из закона ее движения:
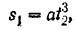
откуда
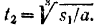
Таким образом, работа силы 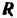 сопротивления среды на данном перемещении тела будет равна
сопротивления среды на данном перемещении тела будет равна
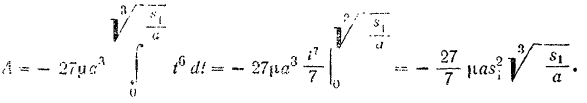
Сила сопротивления среди направлена прогни движения тела потому се работа получилась отрицательной. Чтобы преодолеть эту силу на заданном перемещении тела, надо затратить такую же по величине, но положительную работу.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Дифференциальные уравнения плоского движения твердого тела |
| Элементарная работа силы |
| Графический способ вычисления работы |
| Теорема о работе равнодействующей |
