Оглавление:
Задача разложения вектора по заданным направлениям возможна и имеет единственное решение для векторов на плоскости и для векторов в пространстве.
Векторы на плоскости
Два неколлинеарных упорядоченных вектора на плоскости образуют базис. Они линейно независимы, то есть ни один из них не может быть выражен через другой вектор. Любой третий вектор на плоскости единственным образом может быть представлен в виде линейной комбинации векторов базиса.
Частным случаем базиса на плоскости является пара векторов единичной длины, перпендикулярных друг другу. Они называются ортами и обозначаются 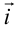 и
и 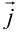 . Совокупность указанного базиса и выбранной точки
. Совокупность указанного базиса и выбранной точки 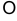 , из которой выходят орты — основа прямоугольных декартовых координат с осями
, из которой выходят орты — основа прямоугольных декартовых координат с осями 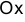 (ось абсцисс),
(ось абсцисс), 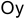 (ось ординат).
(ось ординат).
Совместим начало некоторого произвольного вектора 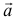 с точкой
с точкой 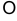 (рисунок 2.4). Из конца вектора
(рисунок 2.4). Из конца вектора 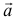 проведем линии, параллельные направлениям векторов
проведем линии, параллельные направлениям векторов 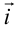 и
и 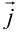 . В точках пересечения этих линий с осями
. В точках пересечения этих линий с осями 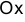 ,
, 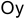 укажем концы вспомогательных векторов
укажем концы вспомогательных векторов 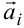 ,
, 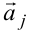 . Вектор
. Вектор 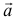 — сумма вспомогательных векторов, так как он является диагональю параллелограмма:
— сумма вспомогательных векторов, так как он является диагональю параллелограмма:
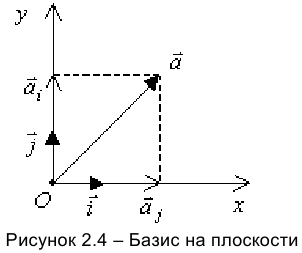
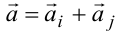 (рисунок 2.4). Векторы
(рисунок 2.4). Векторы 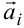 ,
, 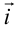 — коллинеарные, следовательно, существует единственное число
— коллинеарные, следовательно, существует единственное число 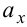 , такое, что
, такое, что 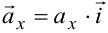 . Аналогично, векторы
. Аналогично, векторы 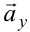 ,
, 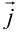 — коллинеарные, следовательно, существует единственное число
— коллинеарные, следовательно, существует единственное число 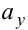 , такое, что
, такое, что 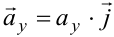 . Из равенства
. Из равенства 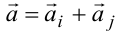 получим разложение вектора
получим разложение вектора 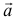 по базису
по базису 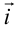 и
и 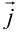 :
:
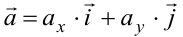
Числа 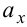 ,
, 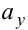 называются координатами вектора
называются координатами вектора 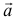 в базисе
в базисе 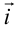 и
и 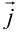 .
.
Векторы в пространстве
Базисом в пространстве называются три любых некомпланарных вектора 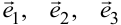 , взятых в определённом порядке.
, взятых в определённом порядке.
Любой четвертый вектор 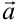 можно представить единственным образом в виде линейной комбинации векторов базиса
можно представить единственным образом в виде линейной комбинации векторов базиса

где 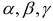 называются координатами вектора в базисе
называются координатами вектора в базисе 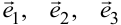 .
.
Вектор базиса нельзя выразить через другие векторы базиса в виде линейной их комбинации. Говорят, что векторы 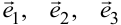 линейно независимы. Добавление любого четвёртого вектора
линейно независимы. Добавление любого четвёртого вектора 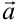 к базисным приводит к выполнению равенства (2.1); говорят, что система векторов
к базисным приводит к выполнению равенства (2.1); говорят, что система векторов 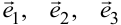 ,
, 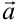 линейно зависима.
линейно зависима.
Частным случаем базиса в пространстве является тройка ортов 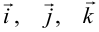 — векторов единичной длины, взаимно перпендикулярных друг другу. Совокупность указанного базиса и выбранной точки
— векторов единичной длины, взаимно перпендикулярных друг другу. Совокупность указанного базиса и выбранной точки 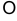 , из которой выходят орты — основа прямоугольных декартовых координат с осями
, из которой выходят орты — основа прямоугольных декартовых координат с осями 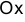 (ось абсцисс),
(ось абсцисс), 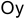 (ось ординат),
(ось ординат), 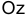 (ось аппликат), (см. рисунок 2.5).
(ось аппликат), (см. рисунок 2.5).
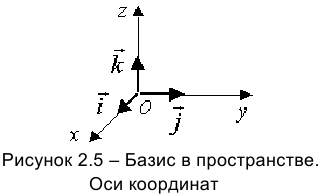
Каждый вектор можно спроектировать на оси координат. Разложение вектора по базису 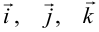 имеет вид:
имеет вид: 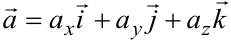 . Здесь
. Здесь 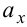 ,
, 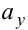 ,
, 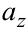 — проекции вектора
— проекции вектора 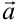 на соответствующие оси координат (координаты вектора).
на соответствующие оси координат (координаты вектора).
Вывод — геометрический вектор на плоскости определяется однозначно двумя числами 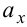 ,
, 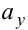 , вектор в пространстве определяется тремя числами
, вектор в пространстве определяется тремя числами 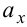 ,
, 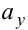 ,
, 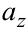 .
.
Если вектор задаётся двумя точками 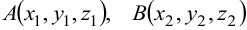 , то координаты вектора
, то координаты вектора 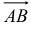 определяются разностями координат конечной и начальной точек:
определяются разностями координат конечной и начальной точек: 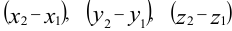 .
.
Длина вектора 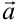 обозначается
обозначается 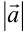 и вычисляется по формуле
и вычисляется по формуле

Если вектор задан своими координатами, то при умножении вектора на число каждая координата умножается на это число:
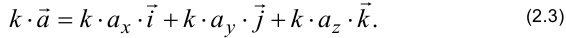
При сложении двух векторов складываются их координаты:
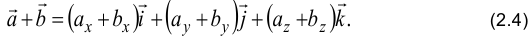
Из свойства 2 операции умножения вектора на число и из формулы (2.3) следует условие коллинеарности векторов. Два вектора 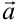 и
и 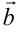 коллинеарные, если пропорциональны их координаты:
коллинеарные, если пропорциональны их координаты:

Пример:
Вектор задан точкой начала 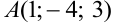 и точкой конца
и точкой конца 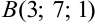 в декартовой системе координат. Определить координаты вектора
в декартовой системе координат. Определить координаты вектора 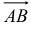 и его длину.
и его длину.
Решение:
Координаты вектора 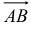 определяем разностями координат конечной и начальной точек:
определяем разностями координат конечной и начальной точек: 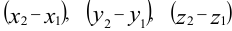 , а именно:
, а именно:
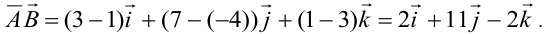
Длину вектора определяем по формуле (2.2):
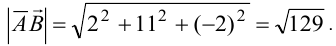
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
