Оглавление:


Регрессия по методу наименьших квадратов: два примера
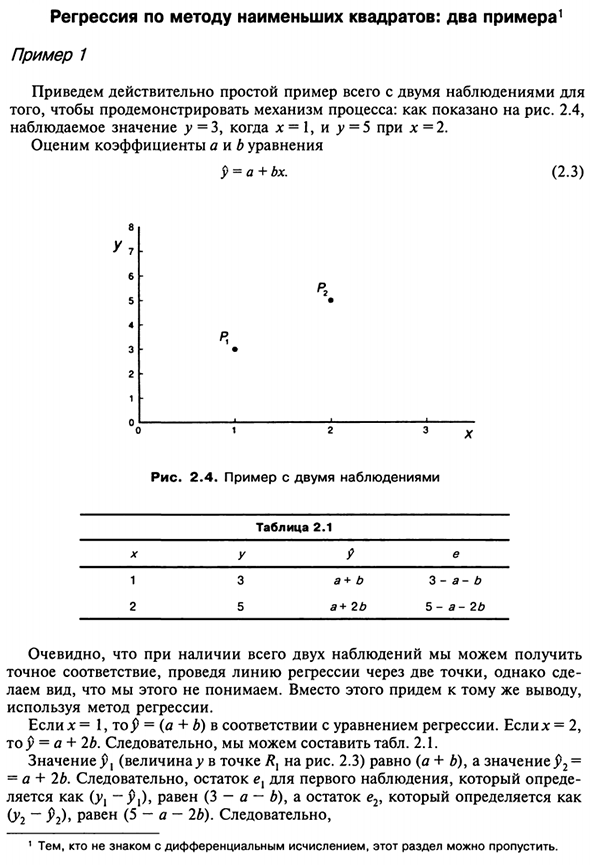
- Регрессия наименьших квадратов: два примера 1 Пример 1 Вот действительно простой пример, который включает в себя следующие два наблюдения: Для демонстрации механизма процесса: 2.4, как показано на рисунке Наблюдения имеют вид y = 3, когда x = 1, и y = 5, когда x = 2.
- Оценить коэффициенты А и В уравнения р = а + бх. (2.3) 8 В L 5 4 В с | 2 1 о Рисунок 2.4. Два примера X 1 2 в 3 5 Таблица 2.1 J> а + б + 2b е B- a- b 5-а-2б Очевидно, что это может быть получено только с двумя наблюдениями. Тем не менее, идеальное совпадение, проведя линию регрессии через две точки Я могу сказать вам, что мы этого не понимаем.
Вместо этого мы приходим к тому же выводу Используйте метод регрессии. Людмила Фирмаль
Если x = 1, P = (a + b) согласно уравнению регрессии. * = 2 у = а + 2б. Следовательно, вы можете создать таблицу. 2.1. Значение y {(точка значения >> /?, Рис. 2.3) равно (a + b), a. значение2 = = а + 2б. Следовательно, остаток е {о первом наблюдении подлежит определению Представляется как (j; 1-j> j), равно (3-a-b), а остаток e2 определяется как: (Y2-j> 2) равно (5-a-2b).
Если вы не знакомы с вычислениями с одной производной, вы можете пропустить этот раздел. 58 S = e2 + e2 = (3-a-b) 2 + (5-a-2b) 2 = = (9 + a2 + b2 -6a-6b + 2ab) + (25 + a2 + 4b2-wa-20b + 4ab) = = 2a2 + 5b2 + 6ab-16a-26b +34. (2.4) Здесь выберите a и b, чтобы значение S было mi По крайней мере. Для этого, используя дифференциальный расчет.
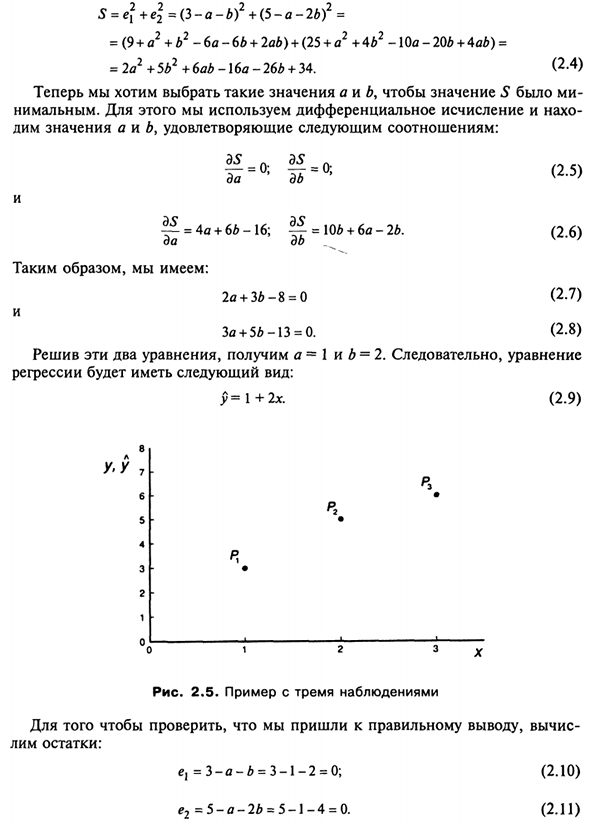
- Укажите значения a и b, которые удовлетворяют следующему соотношению: Да = 0; дБ = 0; (2,5) E5 E5 да Поэтому есть: ^ — = 4a + 6b-16; ^ — = Нет + 6a-2b. б 2a + 36-8 = 0 (2.6) (2.7) + 56-13 = 0 или более (2.8) Решение этих двух уравнений дает a = 1 и b = 2. Следовательно, уравнение Форма регрессии следующая: р = 1 + 2х. (2.9) 8 L Y ‘/ 7 6 5 4 с | — 2 1 0 P * Рисунок 2.5.
Три примера Рассчитать, чтобы подтвердить, что правильный вывод был достигнут остаток остатка: е = 3-а = 3-1-2 = 0; e2 = 5-a-2b = 5-1-4 = 0 (2.U) (2.P) 59 Следовательно, оба остатка равны нулю. Другими словами, линия регрессии Конечно, мы проходим ровно обе точки, которые мы знали с самого начала.
Если есть только два наблюдения, нарисуйте прямую линию, которая проходит через эти две точки. Людмила Фирмаль
В этом случае регрессионный анализ не требуется. Пример 2 Добавьте, используя пример, описанный в предыдущем разделе Одно наблюдение: х = 3 и у = 6. Три наблюдения показаны на рисунке. Не 2.5 Поскольку они находятся на одной линии, они не могут точно совпадать.
В этом случае вам нужно использовать рег Метод наименьших квадратов. Давайте начнем с настройки стандартного уравнения у = а + бх. (2.12) Если значение x равно 1, 2 или 3, рассчитанные значения >> равны. (A + b), (a + 2b) и (a + b) \ Они показаны в таблице. 2.2. X 1 2 3 в 3 5 6 Таблица 2.2 9 а + б + 2b + Zb е 3-а-б 5-а-2b 6-а-б так S = e2 {+ e \ + el = (3-a-b) 2+ (5-a-2b) 2+ (6-a-3b) 2 = = (9 + a2 + b2 -6a-6b + 2ab)
(25 + a2 + 4b2 -I0a-20b + 4ab) + + (36 + a2 + 9b2-I2a-36b + 6ab) = 3a2 + Ш2 + l2ab-2Sa-62b + 70. (2.13) Для условий dS / yes = 0 и dS / db = 0: 6a + 12Z> -28 = 0 (2,14) и 286+ 12a-6 2 = 0. (2.15) Решение этих уравнений дает a = 1,67 и b = 1,50. Поэтому равный Форма регрессии следующая: j> = l, 67 + l, 50x. (2.16
Смотрите также:
| Модель парной линейной регрессии | Детальное рассмотрение остатков |
| Регрессия по методы наименьших квадратов | Регрессия по методу наименьших квадратов с одной независимой переменной |
