Оглавление:






Шар в равномерном поле
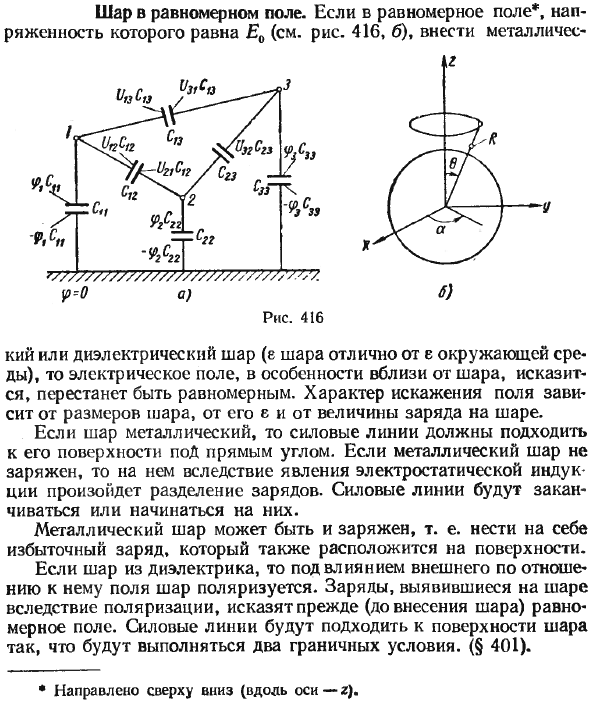
Шар в равномерном поле. Если металлический или диэлектрический шар (шар е отличается от окружающей среды) вводится в однородное электрическое поле * и его напряженность равна Eo (см. Рис. 416, б), электрическое поле, особенно электрическое поле вблизи шара,
- Искаженный и не равномерный. Характер искажения поля зависит от размера шарика, его e и величины заряда на шарике.
Если шар сделан из металла, линии поля должны приближаться к поверхности под прямым углом. Людмила Фирмаль
Когда металлическая сфера не заряжена, в металлической сфере происходит разделение зарядов из-за явления электростатической индукции. Линии электропередач заканчиваются или начинаются с них. Металлические шарики можно заряжать.
То есть он может нести избыточный заряд, который также размещается на поверхности. Если шарик сделан из диэлектрика, он поляризуется под воздействием внешнего поля. Заряд, который появляется на шаре из-за поляризации, искажает однородное поле (до того, как шар введен).
- Линии поля приближаются к поверхности шара и выполняются два граничных условия. (§401). • Ориентировано сверху вниз (вдоль оси z). Эта задача является одной из наиболее типичных «классических» задач. Если шар металлический, то внутри шарика E = 0 и φ = const.
Независимо от того, является ли металлический шар диэлектриком, электрическое поле во внешней области шара описывается уравнением Лапласа, поскольку
во внешней области шара нет свободного заряда. Людмила Фирмаль
Если диэлектрический шарик и свободный заряд на нем равны нулю, электрическое поле внутри шарика также описывается уравнением Лапласа. Поэтому для решения одной и других задач необходимо интегрировать уравнение Лапласа V2q = 0.
Конкретная проблема интегрирования уравнения Лапласа на первом этапе заключается в правильном выборе системы координат. Система координат должна быть выбрана так, чтобы интерфейс внутри поля был описан наиболее удобным образом.
В нашей задаче граница — это сфера. Сфера наиболее удобно описывается в сферической системе координат. Поэтому используйте сферическую систему координат. Второй этап решения заключается в выяснении вопроса о том, является ли исследуемое поле не симметричным.
Условия симметрии поля часто значительно облегчают решение проблемы. В рассматриваемой задаче поле не зависит от координаты a. Чтобы убедиться в этом, выполните следующие действия:
Мысленно проанализируйте поле в плоскости, перпендикулярной оси Z декартовой системы координат и нарисуйте круг на этой плоскости так, чтобы его центр находился на оси Z. Все точки в этом круге имеют одинаковое значение радиуса.
Кроме того, угол меридиана b между радиусом R и осью Z одинаков. Все точки круга находятся в поле в одинаковых условиях. Поэтому их возможности абсолютно одинаковы. Однако характеристики значения угла и положения этой точки окружности различны.
Для набора точек с = const и 0-const и различных значений угла a, если q одинаково, это означает, что φ не зависит от угла a. Таким образом, поле описывается формулой (см. Формулу 13.31): -1 A (sin \ = 0 (13.54) /? 2 dR \ dR I R2 sin 0 d (J \ 00 / (компонент -! — Q)
Уравнение (13.54) является дифференциальным уравнением в частных производных, метод Фурье-Бернулли используется для интегрирования дифференциальных уравнений в частных производных, и в соответствии с методом Фурье-Бернулли решение искомой функции (в данном случае φ) предполагается как произведение.
Две ранее неизвестные функции M и A, одна из которых (A!) Зависит только от R, а другая (A) зависит только от B. Видов функций M и N два Принимая решение в виде произведения функции (13.55), дифференциальное уравнение в частных производных (13.54) можно разделить на два обыкновенных дифференциальных уравнения, одно для Л1 и одно для N.
Альтернатива (13.55) ) (13,54) (p * dM \ I m R2 dR \ dR / ‘R ^ sinbП2 (13,56), умноженное на’ (MN (13,56) (13,57)) уравнения (13,57) Особенность заключается в том, что первый член является функцией только R. Второй член равен только 6. Сумма двух функций зависит только от R, а одна зависит только от 0.
Если пары значений R и 6 бесконечны [уравнение (13.57) подходит для всех точек в поле], то каждая из этих функций равна нулю (13.57 ‘) Или (13,57 «), р — конкретное число. Пока неизвестно. Таким образом, задача сведена к интегралу уравнений (13,57 ‘) и (13,57»).
Общее решение — уравнение ( Уменьшите в зависимости от произведения уравнения (13,57 ‘) на 13,57) и произведения M и N на уравнение (13,57 «). Найдите решение уравнения (13,57’). (13,57 ‘) M — только R
В зависимости от, и N зависит только от 0, поэтому мы можем перейти от частичного дифференцирования к простому дифференцированию: MdR \ dR) их первый интеграл (13.58) m = + l2. Найдите интеграл уравнения: V = Aintg | + A. (13.59)
Поскольку решение не имеет члена A.lntg, покажем, что A3 всегда должно быть равно нулю. Это функция, которая не может быть изменена на бесконечно большое значение через конечные интервалы, и физические соображения показывают, что потенциал в точке оси Z вблизи шара не может быть бесконечным.
С другой стороны, если A3 = / = 0, потенциальное уравнение имеет член / 13lntg. Это равно -co во всех точках, где 6 = 0 (tgG = 0; в tg9 = -oo). 6 == 0 для b-0 Следовательно, конкретное решение y, которое следует из (13.57 ‘), равно (13.60).
Уравнение (13,57 «) (/? 2—) = p ИЛИ MdR \ dR) dR d /? 2 Применить подстановку Эйлера: M = CRn ~ = nCRn ~ *; — = n (n-1) C7? \ «Уравнение 2RnCRn˜1 + II2 (n − 1) nCRn˜2 = pCRnORl * lp = 0. Значение решения p квадратного уравнения (13.61) определяется путем интегрирования второго уравнения (13.57 «).
Решением является выражение A ‘= B cos 0. 2B sin 0 cos 0 Следовательно, число p После нахождения (13.61) и замены на n. Ydem «L-1, N2 = -2. Следовательно, совместное решение уравнения (13.57») дает следующую формулу для CP 🙁 В 13.62 есть четыре неизвестных константы CLT C2, C3 и C4) (13.62)
Значение константы зависит от шара (проводящего или диэлектрического), введенного в поле *. Задачи теории поля, которые требуют решения уравнений в частных производных и выбора решений, удовлетворяющих граничным условиям из большого числа решений, обычно называют краевыми задачами в математической работе.
Смотрите также:
| Емкостные коэффициенты. Вторая группа формул Максвелла. | Проводящий шар в равномерном поле. |
| Частичные емкости. Третья группа формул Максвелла. | Диэлектрический шар в равномерном поле. |
Если вам потребуется заказать решение по электротехнике (ТОЭ) вы всегда можете написать мне в whatsapp.
