Оглавление:
Свойства сходящихся последовательностей
- Сходящаяся последовательность имеет единственный предел.
- Всякая подпоследовательность сходящейся последовательности сходится к тому же пределу.
- Сходящаяся последовательность ограничена.
- Если последовательность
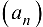имеет предел 
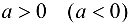, то, начиная с некоторого номера 
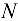. выполняется неравенство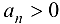 
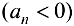, т. е. члены последовательности сохраняют знак числа 
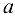. - Пусть
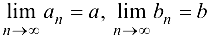и, начиная с некоторого номера 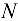, выполняется неравенство 
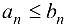, тогда 
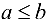. - Пусть для последовательностей
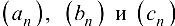выполнены неравенства 
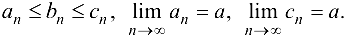. Тогда 
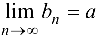. - Если последовательности
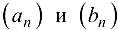сходятся и 
, 
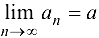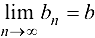, то:
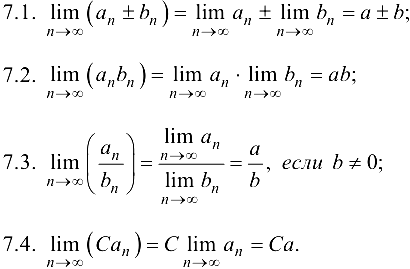
Таким образом, согласно свойству 7, арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами.
На основании свойства 2 можно получить условие расходимости последовательности.
Следствие 2.2*. Если из последовательности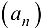 
можно выделить две подпоследовательности 
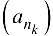сходящиеся к 
, 
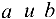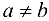, то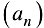 
не имеет предела.
Пример 2.6.
Доказать, что последовательность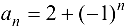 
не имеет предела.
Решение:
Выделим из исходной последовательности две подпоследовательности:
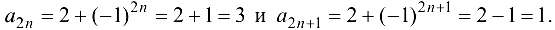
Так как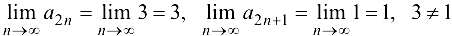 
то исходная последовательность не имеет предела.
Замечание 2.1. Обратное к свойству 3, вообще говоря, не верно, т. е. ограниченная последовательность может не быть сходящейся.
Определение 2.9. Последовательность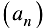
называется:
- возрастающей, если
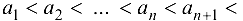…; - неубывающей, если
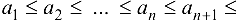…; - убывающей, если
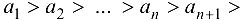… ; - невозрастающей, если
…
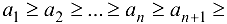Все указанные последовательности называются также монотонными, а возрастающая и убывающая последовательности — строго монотонными.
Теорема 2.3. Для того чтобы монотонная последовательность сходилась, необходимо и достаточно, чтобы она была ограниченной.
Доказательство.
Необходимость. Согласно свойству 3, всякая сходящаяся последовательность ограничена.
Достаточность. Пусть 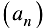монотонно неубывающая ограниченная сверху последовательность, т. е. 
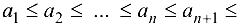и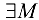 
такое, что 
.
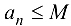Рассмотрим числовое множество А, состоящее из элементов данной последовательности. Это множество ограничено сверху и непусто. Поэтому А имеет точную верхнюю грань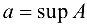 
. Тогда, по определению 
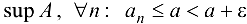. Так как 
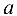— точная верхняя грань множества элементов последовательности 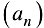, то для 
, такой, что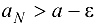 
, и так как последовательность 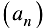неубывающая, то при 
.
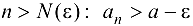Таким образом,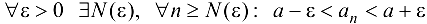 
, т. е. 
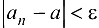. А это и означает, что число а — предел последовательности .
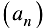Аналогично доказывается случай монотонно невозрастающей последовательности. ■
Замечание 2.2. На основании данной теоремы можно доказать существование предела последовательности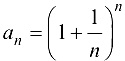 
, а именно 
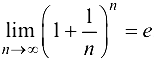, где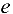 
(число Эйлера) — иррациональное число,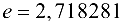 
Теорема 2.4* (Больцано-Вейерштрасса). Из всякой ограниченной последовательности чисел можно выделить сходящуюся подпоследовательность.
Определение 2.10. Совокупность отрезков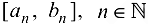 
, образует систему вложенных отрезков, если выполнены следующие условия:
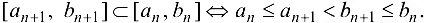
Система вложенных отрезков будет системой стягивающихся отрезков, если
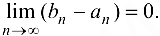
Теорема 2.5 (Кантора). Всякая последовательность вложенных стягивающихся отрезков имеет единственную общую точку, принадлежащую всем отрезкам.
Доказательство.
Из (2.2) следует, что монотонные последовательности концов отрезков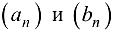 
сходятся, причем из равенства (2.3):
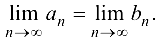
Тогда
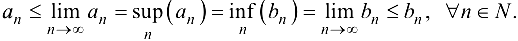
Из теоремы 2.3 следует, что общей точкой, принадлежащей отрезкам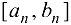 
является
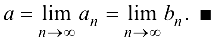
Пример 2.7.
Найти предел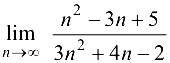 
.
Решение:
Ответ: 
.
Пример 2.8.
Найти предел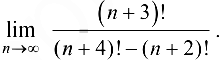 
.
Решение:
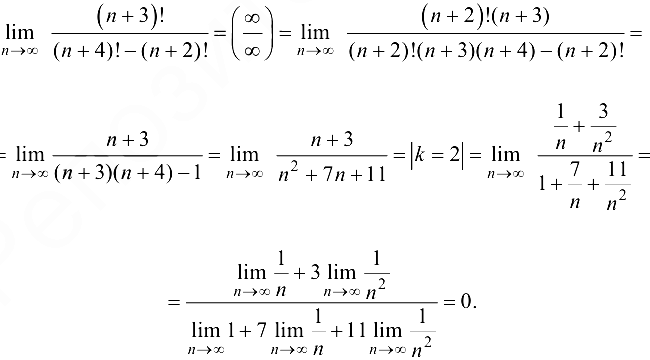
Ответ: 0.
Пример 2.9.
Найти предел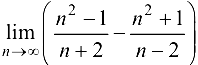 
.
Решение:
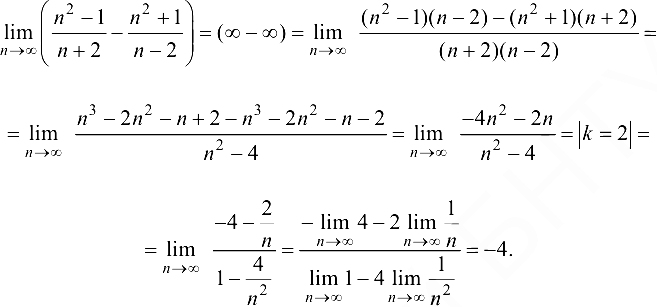
Ответ: -4.
Пример 2.10.
Найти предел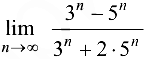 
.
Решение:
Ответ: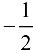 
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
