Оглавление:









Целочисленное линейное программирование
- Полное линейное программирование Постановка проблемы. Со многими оптимальными задачами Незапланированное значение — это количество единиц Та или иная техника, автомобиль, скот и т. Д. То есть они являются абсолютно неделимыми величинами. В этом случае Сама неизвестная задача должна быть целым числом. Задание Оптимальный план с требованиями.
- Все или некоторые целые числа переменных называются задачами Целочисленное программирование. Возьмите проблему минимизации функций в качестве стандарта Ζ = Σ * / * / (1) В условиях η Σajx§ = ni = 1 »2, …, m \ (2) x,> 0, / = 1,2 л; (3) xf — целое число, / = 1, 2 nx (n \ …, xa и Перенумерован от 1 до n . Если n \ = n, задача (1) — (4) называется полностью Целое, иначе (fii 0, f = 1, 2, 3; *, -— все Число (у = 1, 2, 3).
Из огромного количества видов Из этих задач рассмотрим целочисленную линейную задачу Программирование. Людмила Фирмаль
Без целочисленного условия вы можете найти лучший план для этой проблемы / 1 9 \ Симплекс метод и т.д! 0ητ = [~ 2 ‘°> «2 * 1 ・ Округление координат дает вектор X = (0, 0, 4) Это также верно для целочисленных задач. Искал после Целочисленное оптимальное решение таково, что JΠΤ0Jι = = (2, 2, 5). Давайте рассмотрим некоторые классические целочисленные примеры Линейная задача.
Проблема с рюкзаком. Турист готовится к длительной поездке В горах С рюкзаком он может нести багаж, который не такой большой Больше действует. Этот груз может состоять из предметов η типа, Каждый элемент типа / имеет массу af kg (/ = 1, 2, …, n). для Каждый тип туриста устанавливает значение ср Время в пути Количество предметов каждого типа х $ Все в сумме, поэтому вы должны положить его в рюкзак Оборудование максимально?
Модель для этой задачи: η Ζ = 5j cixl- * max / «Ι η При ограничении 2β / * / xt> ®> χι-> eJloe (/ = U 2, …, η). / = ι Проблема с коммивояжером. Есть п + 1 город. Матричный набор C = (cj /) расстояние между городами. Оставьте источник В голубом городе продавец должен идти ко всем остальным Вернитесь в город и вернитесь в тот же город. Решите, в каком порядке перенести город для следующей цели Общее расстояние поездки было минимальным.
В следующих случаях переменная, равная 1, обозначается xz. Продавец перемещается из города У в город Л /, иначе 0 Случай. Математическая модель задачи: nη Ζ = ΣΣ, чтобы минимизировать общее расстояние перемещения ί = 0 / = 0 Следующие условия: 1) Продавец покидает каждый город η Только один раз: Σ ^ = 1 0 = 1 »2, …, l); 2) Продавец / = о η Введите каждый город один раз, кроме первого города: J] хц = я = 0 = r 1 (/ = 1, 2, …, / r); 3)
Пропуск продавца состоит из одного Замкнутый цикл: u-u + pkc Посещение города На м-м этапе. В итоге ты-ж / < <r-1 равно * ί / = 0. Если xt = 1, третье условие выполнено Принимается как строгое равенство. u-n + phu = m- (m + 1) + n = n-1. Для задач линейного целочисленного программирования Мы разработали много способов их решения.
Эти методы включают Также называется методом отсечения. Список легко Соображения, которые лежат в основе этих методов. L обозначает множество приемлемых решений проблемы (1) — (3) и через Ln выпуклый линейный корпус (т.е. Набор всех линейных выпуклых комбинаций) Целая точка Л. Очевидно, Лу будет целым числом Многогранник (то есть многогранник вершины).
Целочисленные координаты), множество базисных решений Включено в Л. Тогда мы можем доказать следующую теорему. Теорема 1. Когда X — оптимальное базовое решение задачи в плМногогранные условия Лу и Чи Наилучшее решение задачи (1) — (4). Это лучший первый Решение задачи Χι (1) — (4) Например, без условного целого ™ Симплексный метод. Затем, если не соответствует, построить Линейные ограничения.
Он является целочисленным решением задачи (1) — (4) и не удовлетворяет решению Χχ. Геометрически это означает рисование сечения (гиперплоскости) Многогранник L для отбрасывания нецелых Вершина чи, не затрагивая оставшиеся целые числа, такие как Этот раздел обычно называется правильным. Добавить это линейное ограничение к ограничению задачи (1) — (3) новый оптимум симплекс-методом Решения и т. Д.
Желательно после нескольких таких итераций Целая точка находится на границе разрешенного множества Решение и одно из таких оптимальных решений Целое число Указывает точное определение правильного отсечения. вырезка Σα / # /> αο (α> Χ> «о) (5) Считается правильным, если он удовлетворяет следующим двум условиям: условия: Я) Условие отсечения. Оптимальное решение для линейных задач (1) — (3) не удовлетворяет условию отсечки (5). olXl <αο. (6) II)
Требования к точности. Приемлемое решение Целочисленная задача удовлетворяет неравенству (5). aX> a0. (7) Вспомните следующие понятия: Все [l:] Вещественное число χ называется наибольшим целым числом, Не превышать х. Дробная часть ({*}) числа χ называется Число {х} = х- [х]. Таким образом, метод отсечения основан на двух Основные идеи: 1) Многоступенчатое линейное приближение Целочисленная задача.
2) Переход от этапа к этапу с использованием правильного этапа Отсечение. Чтобы реализовать эти идеи, нужно показать такие вещи Как правильно построить отсечение, чтобы обеспечить Конечность процесса принятия решения. И в дополнение к этому, это необходимо Практикуйте приемы, которые не разрешены Чрезмерное увеличение количества правильных срезов дел.
- Если процесс принятия решения является долгим. То же самое В некоторых случаях вам необходимо принять меры для уменьшения размера. Промежуточное целочисленное задание. Второй алгоритм Гомори. Как решение Задача (1) — (4) Так называемый второй документ Алгоритм Гомори. Этот метод отличается от первого алгоритма Гомори, может быть решена полностью и частично Целочисленная задача.
Особенно большинство потребностей Для нормализации задачи, дополнительные Целочисленные переменные обязательно указывают на важность Как решить частично целочисленную задачу. Кроме этого При решении целой целой задачи, как показано.
Практика, нет никаких причин, чтобы расставить приоритеты один из двух Алгоритм Гомори * Людмила Фирмаль
Второй алгоритм Гомори 1) Коэффициент С / целевой функции (1) является целым числом С номерами. В противном случае минимум Общее кратное знаменателя q \ 2) Целевая функция (1) Ограничено приемлемым решением набора L \ 3) Множество L ограничено. В основе описанного метода решения задачи (1) — (4) лежит Как правильно построить отсечение.
Такой раздел построен BGex итерация метода: начальный, нулевой, первый и т. Д. На первом шаге предположим, что симплектическая таблица Ts имеет элемент x \ h. Где х? £ — значение базовой переменной. Лучшее решение Предположим, у вас есть вектор X. Например, базовая переменная xlr = x10 не является целым числом. Теорема 2. Определите числа a <> и a / с уравнениями «O = U.b (8) 130 о, = < {4 /} если / {a: /. }; if /> / t | + 1 и *>,> 0; (9)
Тогда неравенство (- * H)> if /> «v + 1 и * / | <0 Σα / # /> α0ι 7 ^ с (U) Где Ns — значение индекса, установленное / неосновный случай Переменная является правильным отсечением. Доказательство. Сначала проверьте статус отсечения. Σct / Я / = Σα / 0 = 0 <α0 = (x / J, После этого выполняется условие отсечения. Чтобы подтвердить правильное состояние отсечки, Расширение неосновной базовой переменной xf х! = xsSio + Σ * ‘/ (- * /).
ŽNK Дай мне s} Xf j € Nsf /> m + l; Где yri — целое число, значение которого выбрано Позже. тогда — —ЛЛ + ΣYn — Xi = {χ! , } + Σat (—χι), Это WJ + Σ (-Xrf) xi = Zr (x), Где Zr (x) — это целое. Пусть Nf и N7 — множество этих чисел / € iV Xn <0 и xri> 0 и S + <*) = Σ (- * r /) * /> 0; S до (x) = Σ (-Xr /) x, <0 Такое же неравенство можно переписать так: «-№ S + (x)> 0, (11) S- (x)> 0. (12) Используйте введенную запись, чтобы получить: UU + S + (x) -ST (χ) = Zr (χ), Ζ, (χ) — целые числа.
Есть два возможных случая: 1) S + (x) + S- (x)> 0; 2) S + (x) + S до (x) <0. Во-первых, держите случай 1). Далее Zr (χ)> [xf9} И целое число х! благодаря aZr (*)> 0, благодаря Integer ™ Μ *) M )> 1. Следовательно, S + (x) + S ~ (x)> 1- {4} Или (см. 12) S + (x)> 1 — { /,}. Перепишите последнее неравенство вида T ^ S + ()> { U- (13) Предположим, что имеет место Случай 2). Далее Zr (x) <{? „} И Целое число Zr (x) Zr (x) <0 Следовательно, {x? A} + S + (*) + S ~~ (χ) <0.
Учитывая (11), -s — (*)> W;}. (Η) Сочетание неравенства (12) и (13) в случае 1) и случае 2) Неравенства (11) и (14), HL + (x) -s- ()> U.b Или то же самое м Для ~ Форма этого неравенства Σ <* / * /> {* / ・}>, где 0 и a / = = <* / (# //) (/ <Λι) «и правая часть {* / 0} не зависит от yη. Рассмотрите причину и необходимость максимально возможного отсечения Область L выполнимого решения линейной задачи.
Вы должны выбрать так, чтобы / (г / г /) было как можно меньше. xi / = xsrJ-yrh j € Ns; j 0; Когда Xr / -ί / r /, #r / — ** / <0. Если xsri является целым числом, yrj = # * / / = 0 получается. вес Тогда xTi не является целым числом, min {^ b ^ «4i), yri ~ 4l> °} = ~ ^ RT ° ~~ u,]) ‘ min \ {xsrl-yri), если lxri-η> 0} = {χ% . Следовательно, α, = minΙγζ ^ Π (1 ~ W> ・ No. 1 ・ Удобнее переписать это же выражение в следующем формате: {> £ /}. если {4j) <{? }; K} а = 0 — {* /}) ・
She ™ (* ‘/)> R} ・ наконец (-I- (1 .- {;,}), / <Я1, { ・,}> {<); к ■ (- * м. Теорема доказана. Последовательность действий для описанного метода следующая: 1) Начальная итерация. Где (1) — (3) линейный вопрос Программирование. Если эта проблема может быть решена, она может быть решена И целочисленная задача (1) — (4). Кроме того, Integer ™ необходимых компонентов полученного раствора.
Это также лучшее решение для задач (1) — (4). если Xl не удовлетворяет условию (4), поэтому оно должно стремиться к нулю Повторите 2) Sth итерация (s> 0). Лучшее решение Задача (1) — (3) С дополнительными условиями отсечки Удовлетворяет целочисленное условие (4). следующий Соответствующая симплекс-таблица нецелая Базовая переменная (например, £ 0 0) субъект (детерминированный).
Самый низкий серийный номер. Построить правильное ограничение (10) для этой переменной. Его коэффициент определяется уравнениями (8) — (9). ограничение Где s — количество итераций. Преобразовать (11) в форму 2j <ήχ} — * β + ί4-ι = αθιXn + s + i> 0. (17) Добавьте это следующее ограничение к (3), чтобы решить Построена задача (1) — (3), получено новое оптимальное решение Xl.s + i * или убедился в несостоятельности встроенного.
Так в оригинальной задаче. Ограничение (17) должно быть назначено таблице Ts снизу. Новая таблица содержит недопустимую строку Yal-fs + i Основное решение. Применить двойной симплекс-метод Используйте эту таблицу, чтобы быстро получить лучшее решение. После получения из базового решения переменная xn + s + \ Удалить соответствующую строку в таблице и после ввода.
В дополнение к основному решению этой переменной, которая При замене #n + s + b указанная строка не восстанавливается. Если решение XLt s + i не удовлетворяет условию (4), Перейти к (s + 1) -й итерации. «» Мы можем доказать конечность следующего алгоритма Гомори. Следующие условия: 1) Коэффициент целевой функции составляет С целым числом функция ограничена ниже множества L.
Первое требование заключается в том, чтобы все переменные Введите в задачу целевую функцию Z, а также саму целевую функцию Должно быть целым числом. Целое число Ζ считается При построении правильного раздела. 2) Допустимый набор Ln Решение задачи (1) — (4) не является пустым.
Пример. Максимизировать линейную форму 2 = 6 * ^ + 8 * 2 в условиях -7xx + 4×2 <и; 2χχ + 2×2 <9; Xf> 0; x2> 0; * и x2 — целые числа. Мы принимаем проблему к ее стандартной форме. Минимизировать функцию ^ Z = = -6хх- с ограничениями 8х2-1хг + 4х2 + х3 = 14; 2x ± + 2×2 + chl = 9; Hu> 0; j = 1, 2, 3, 4; xg и x2 — целые числа. Найдите лучшее решение для вашей проблемы (см. Таблицу 0-5).
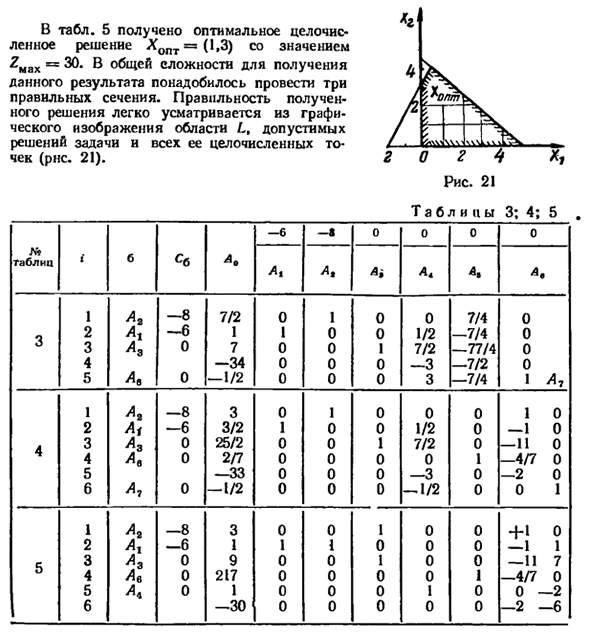
В таблице. 5 Оптимальный прием Целочисленное решение анализа ядерной безопасности = (1,3) и значение £ max = 30. Всего Этот результат требуется 3 Правильный раздел. правильность Полученное решение Графическое представление области L, приемлемо Решение задачи и все ее целые числа Точка (около 21).
Смотрите также:
Решение задач по математическому программированию
